
Künneth theorem
Encyclopedia
In mathematics
, especially in homological algebra
and algebraic topology
, a Künneth theorem is a statement relating the homology
of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology
of two topological space
s X and Y and their product space X × Y. In the simplest possible case the relationship is that of a tensor product
, but for applications it is very often necessary to apply certain tools of homological algebra to express the answer.
A Künneth theorem or Künneth formula is true in many different homology and cohomology theories, and the name has become generic. These many results are named for the German mathematician Hermann Künneth.
es, then this can be replaced by cellular homology
, because that is isomorphic to singular homology. The simplest case is when the coefficient ring for homology is a field F. In this situation, the Künneth theorem (for singular homology) states that for any integer k,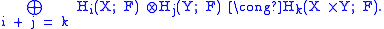
Furthermore, the isomorphism is a natural isomorphism. The map from the sum to the homology group of the product is called the cross product. More precisely, there is a cross product operation by which an i-cycle on X and a j-cycle on Y can be combined to create an (i+j)-cycle on X × Y; so that there is an explicit linear mapping defined from the direct sum to Hk(X × Y).
A consequence of this result is that the Betti number
s, the dimensions of the homology with Q coefficients, of X × Y can be determined from those of X and Y. If pZ(t) is the generating function
of the sequence of Betti numbers bk(Z) of a space Z, then
Here when there are finitely many Betti numbers of X and Y, each of which is a natural number
rather than ∞, this reads as an identity on Poincaré polynomials. In the general case these are formal power series
with possibly infinite coefficients, and have to be interpreted accordingly. Furthermore, the above statement holds not only for the Betti numbers but also for the generating functions of the dimensions of the homology over any field. (If the integer homology is not torsion-free then these numbers may differ from the standard Betti numbers.)
. This case is particularly important because the integers are a PID.
are a PID.
In this case the equation above is no longer always true. A correction factor appears to account for the possibility of torsion phenomena. This correction factor is expressed in terms of the Tor functor
, the first derived functor
of the tensor product.
When R is a PID, then the correct statement of the Künneth theorem is that for any topological spaces X and Y there are natural short exact sequences
Furthermore these sequences split, but not canonical
ly.

with integer coefficients of the product RP2 x RP2 of two real projective planes. These spaces are CW complexes. Denoting the homology group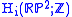 by hi for brevity's sake, one knows from a simple calculation with cellular homology
by hi for brevity's sake, one knows from a simple calculation with cellular homology
that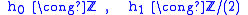
and hi is zero for all other values of i. The only non-zero Tor group
(torsion product) which can be formed from these values of hi is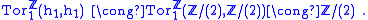
Therefore the Künneth short exact sequence reduces in every degree to an isomorphism, because there is a zero group in each case on either the left or the right side in the sequence. The result is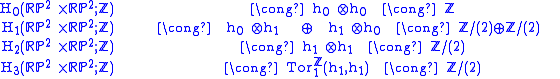
and all the other homology groups are zero.

In the cases described above, this spectral sequence collapses to give an isomorphism or a short exact sequence.
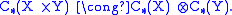
For singular chains this is the theorem of Eilenberg and Zilber
. For cellular chains on CW complexes, it is a straightforward isomorphism. Then the homology of the tensor product on the right is given by the spectral Künneth formula of homological algebra.
The freeness of the chain modules means that in this geometric case it is not necessary to use any hyperhomology or total derived tensor product.
There are analogues of the above statements for singular cohomology and sheaf cohomology. For sheaf cohomology on an algebraic variety, Grothendieck found six spectral sequences relating the possible hyperhomology
groups of two chain complexes of sheaves and the hyperhomology groups of their tensor product.
. The homotopy category of such modules closely resembles the derived categories of homological algebra.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
and algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a Künneth theorem is a statement relating the homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
of two topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s X and Y and their product space X × Y. In the simplest possible case the relationship is that of a tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
, but for applications it is very often necessary to apply certain tools of homological algebra to express the answer.
A Künneth theorem or Künneth formula is true in many different homology and cohomology theories, and the name has become generic. These many results are named for the German mathematician Hermann Künneth.
Singular homology with coefficients in a field
Let X and Y be two topological spaces. In general one uses singular homology; but if X and Y happen to be CW complexCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es, then this can be replaced by cellular homology
Cellular homology
In mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
, because that is isomorphic to singular homology. The simplest case is when the coefficient ring for homology is a field F. In this situation, the Künneth theorem (for singular homology) states that for any integer k,
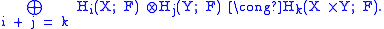
Furthermore, the isomorphism is a natural isomorphism. The map from the sum to the homology group of the product is called the cross product. More precisely, there is a cross product operation by which an i-cycle on X and a j-cycle on Y can be combined to create an (i+j)-cycle on X × Y; so that there is an explicit linear mapping defined from the direct sum to Hk(X × Y).
A consequence of this result is that the Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s, the dimensions of the homology with Q coefficients, of X × Y can be determined from those of X and Y. If pZ(t) is the generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
of the sequence of Betti numbers bk(Z) of a space Z, then
Here when there are finitely many Betti numbers of X and Y, each of which is a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
rather than ∞, this reads as an identity on Poincaré polynomials. In the general case these are formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
with possibly infinite coefficients, and have to be interpreted accordingly. Furthermore, the above statement holds not only for the Betti numbers but also for the generating functions of the dimensions of the homology over any field. (If the integer homology is not torsion-free then these numbers may differ from the standard Betti numbers.)
Singular homology with coefficients in a PID
The above formula is simple because vector spaces over a field have very restricted behavior. As the coefficient ring becomes more general, the relationship becomes more complicated. The next simplest case is the case when the coefficient ring is a principal ideal domainPrincipal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
. This case is particularly important because the integers
 are a PID.
are a PID.In this case the equation above is no longer always true. A correction factor appears to account for the possibility of torsion phenomena. This correction factor is expressed in terms of the Tor functor
Tor functor
In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology....
, the first derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
of the tensor product.
When R is a PID, then the correct statement of the Künneth theorem is that for any topological spaces X and Y there are natural short exact sequences

Furthermore these sequences split, but not canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
ly.
Example
The short exact sequences just described can easily be used to compute the homology groups
with integer coefficients of the product RP2 x RP2 of two real projective planes. These spaces are CW complexes. Denoting the homology group
 by hi for brevity's sake, one knows from a simple calculation with cellular homology
by hi for brevity's sake, one knows from a simple calculation with cellular homologyCellular homology
In mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
that
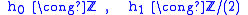
and hi is zero for all other values of i. The only non-zero Tor group
Tor functor
In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology....
(torsion product) which can be formed from these values of hi is
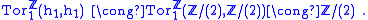
Therefore the Künneth short exact sequence reduces in every degree to an isomorphism, because there is a zero group in each case on either the left or the right side in the sequence. The result is
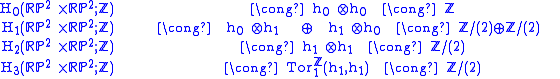
and all the other homology groups are zero.
The Künneth spectral sequence
For a general commutative ring R, the homology of X and Y is related to the homology of their product by a Künneth spectral sequenceSpectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...

In the cases described above, this spectral sequence collapses to give an isomorphism or a short exact sequence.
Relation with homological algebra, and idea of proof
The chain complex of the space X × Y is related to the chain complexes of X and Y by a natural quasi-isomorphismQuasi-isomorphism
In homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
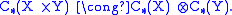
For singular chains this is the theorem of Eilenberg and Zilber
Eilenberg–Zilber theorem
In mathematics, specifically in algebraic topology, the Eilenberg–Zilber theorem is an important result in establishing the link between the homology groups of a product space X \times Y and those of the spaces X and Y. The theorem first appeared in a 1953 paper in the American Journal of...
. For cellular chains on CW complexes, it is a straightforward isomorphism. Then the homology of the tensor product on the right is given by the spectral Künneth formula of homological algebra.
The freeness of the chain modules means that in this geometric case it is not necessary to use any hyperhomology or total derived tensor product.
There are analogues of the above statements for singular cohomology and sheaf cohomology. For sheaf cohomology on an algebraic variety, Grothendieck found six spectral sequences relating the possible hyperhomology
Hyperhomology
In homological algebra, the hyperhomology or hypercohomology of a complexof objects of an abelian category is an extension of the usual homology of an object to complexes....
groups of two chain complexes of sheaves and the hyperhomology groups of their tensor product.
Künneth theorems in generalized homology and cohomology theories
There are many generalized or extraordinary homology and cohomology theories for topological spaces. K-theory and cobordism are the best-known. Their striking common feature (not their definition) is that they do not arise from ordinary chain complexes. Thus Künneth theorems can not be obtained by the above methods of homological algebra. Nevertheless Künneth theorems in just the same form have been proved in very many cases by various other methods. The first were Atiyah's Künneth theorem for complex K-theory and Conner and Floyd's result in cobordism. A general method of proof emerged, based upon a homotopical theory of modules over highly structured ring spectraSpectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
. The homotopy category of such modules closely resembles the derived categories of homological algebra.


