
Diagonal functor
Encyclopedia
In category theory
, for any object in any category
in any category
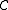 where the product
where the product
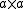 exists, there exists the diagonal morphism
exists, there exists the diagonal morphism
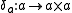
satisfying
 for
for 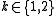 ,
,
where is the canonical projection morphism to the
is the canonical projection morphism to the 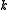 -th component. The existence of this morphism is a consequence of the universal property
-th component. The existence of this morphism is a consequence of the universal property
which characterize
s the product (up to
isomorphism
). The restriction to binary products here is for ease of notation; diagonal morphisms exist similarly for arbitrary products. The image
of a diagonal morphism in the category of sets
, as a subset
of the Cartesian product
, is a relation
on the domain, namely equality.
For concrete categories, the diagonal morphism can be simply described by its action on elements of the object
of the object  . Namely,
. Namely, 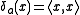 , the ordered pair
, the ordered pair
formed from . The reason for the name is that the image
. The reason for the name is that the image
of such a diagonal morphism is diagonal (whenever it makes sense), for example the image of the diagonal morphism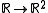 on the real line
on the real line
is given by the line which is a graph
of the equation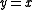 . The diagonal morphism into the infinite product
. The diagonal morphism into the infinite product 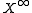 may provide an injection
may provide an injection
into the space of sequences valued in ; each element maps to the constant sequence
; each element maps to the constant sequence
at that element. However, most notions of sequence spaces have convergence restrictions which the image of the diagonal map will fail to satisfy.
In particular, the category of small categories
has products, and so one finds the diagonal functor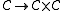 given by
given by  , which maps objects as well as morphisms. This functor
, which maps objects as well as morphisms. This functor
can be employed to give a succinct alternate description of the product of objects within the category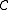 : a product
: a product 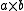 is a universal arrow from
is a universal arrow from 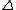 to
to 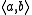 . The arrow comprises the projection maps.
. The arrow comprises the projection maps.
More generally, in any functor category
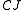 (here
(here 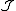 should be thought of as a small index category), for each object
should be thought of as a small index category), for each object  in
in 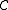 , there is a constant functor with fixed object
, there is a constant functor with fixed object  :
: 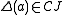 . The diagonal functor
. The diagonal functor 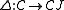 assigns to each object of
assigns to each object of  the functor
the functor 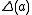 , and to each morphism
, and to each morphism 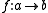 in
in 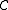 the obvious natural transformation
the obvious natural transformation
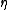 in
in 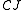 (given by
(given by 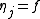 ). In the case that
). In the case that 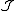 is a discrete category with two objects, the diagonal functor
is a discrete category with two objects, the diagonal functor 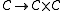 is recovered.
is recovered.
Diagonal functors provide a way to define limits
and colimits of functors. The limit of any functor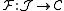 is a universal arrow from
is a universal arrow from 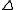 to
to 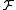 and a colimit is a universal arrow
and a colimit is a universal arrow 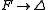 . If every functor from
. If every functor from 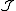 to
to 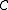 has a limit (which will be the case if
has a limit (which will be the case if 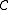 is complete), then the operation of taking limits is itself a functor from
is complete), then the operation of taking limits is itself a functor from 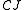 to
to 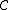 . The limit functor is the right-adjoint
. The limit functor is the right-adjoint
of the diagonal functor. Similarly, the colimit functor (which exists if the category is cocomplete) is the left-adjoint of the diagonal functor. For example, the diagonal functor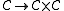 described above is the left-adjoint of the binary product functor
described above is the left-adjoint of the binary product functor
and the right-adjoint of the binary coproduct functor
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, for any object
 in any category
in any categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
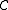 where the product
where the productProduct (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
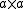 exists, there exists the diagonal morphism
exists, there exists the diagonal morphism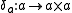
satisfying
 for
for 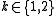 ,
,where
 is the canonical projection morphism to the
is the canonical projection morphism to the 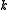 -th component. The existence of this morphism is a consequence of the universal property
-th component. The existence of this morphism is a consequence of the universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
which characterize
Characterization (mathematics)
In mathematics, the statement that "Property P characterizes object X" means, not simply that X has property P, but that X is the only thing that has property P. It is also common to find statements such as "Property Q characterises Y up to isomorphism". The first type of statement says in...
s the product (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
). The restriction to binary products here is for ease of notation; diagonal morphisms exist similarly for arbitrary products. The image
Image (category theory)
Given a category C and a morphismf\colon X\to Y in C, the image of f is a monomorphism h\colon I\to Y satisfying the following universal property:#There exists a morphism g\colon X\to I such that f = hg....
of a diagonal morphism in the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, as a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
, is a relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
on the domain, namely equality.
For concrete categories, the diagonal morphism can be simply described by its action on elements
 of the object
of the object  . Namely,
. Namely, 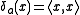 , the ordered pair
, the ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
formed from
 . The reason for the name is that the image
. The reason for the name is that the imageImage (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of such a diagonal morphism is diagonal (whenever it makes sense), for example the image of the diagonal morphism
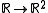 on the real line
on the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is given by the line which is a graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of the equation
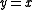 . The diagonal morphism into the infinite product
. The diagonal morphism into the infinite product 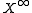 may provide an injection
may provide an injectionInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
into the space of sequences valued in
 ; each element maps to the constant sequence
; each element maps to the constant sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
at that element. However, most notions of sequence spaces have convergence restrictions which the image of the diagonal map will fail to satisfy.
In particular, the category of small categories
Category of small categories
In mathematics, specifically in category theory, the category of small categories, denoted by Cat, is the category whose objects are all small categories and whose morphisms are functors between categories...
has products, and so one finds the diagonal functor
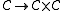 given by
given by  , which maps objects as well as morphisms. This functor
, which maps objects as well as morphisms. This functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
can be employed to give a succinct alternate description of the product of objects within the category
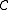 : a product
: a product 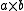 is a universal arrow from
is a universal arrow from 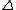 to
to 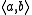 . The arrow comprises the projection maps.
. The arrow comprises the projection maps.More generally, in any functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
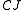 (here
(here 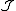 should be thought of as a small index category), for each object
should be thought of as a small index category), for each object  in
in 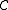 , there is a constant functor with fixed object
, there is a constant functor with fixed object  :
: 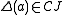 . The diagonal functor
. The diagonal functor 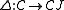 assigns to each object of
assigns to each object of  the functor
the functor 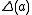 , and to each morphism
, and to each morphism 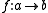 in
in 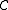 the obvious natural transformation
the obvious natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
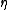 in
in 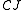 (given by
(given by 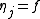 ). In the case that
). In the case that 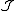 is a discrete category with two objects, the diagonal functor
is a discrete category with two objects, the diagonal functor 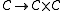 is recovered.
is recovered.Diagonal functors provide a way to define limits
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
and colimits of functors. The limit of any functor
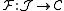 is a universal arrow from
is a universal arrow from 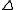 to
to 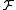 and a colimit is a universal arrow
and a colimit is a universal arrow 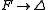 . If every functor from
. If every functor from 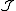 to
to 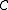 has a limit (which will be the case if
has a limit (which will be the case if 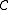 is complete), then the operation of taking limits is itself a functor from
is complete), then the operation of taking limits is itself a functor from 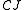 to
to 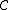 . The limit functor is the right-adjoint
. The limit functor is the right-adjointAdjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
of the diagonal functor. Similarly, the colimit functor (which exists if the category is cocomplete) is the left-adjoint of the diagonal functor. For example, the diagonal functor
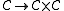 described above is the left-adjoint of the binary product functor
described above is the left-adjoint of the binary product functorProduct (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
and the right-adjoint of the binary coproduct functor
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
.

