Chain (algebraic topology)
Encyclopedia
In algebraic topology
, a simplicial k-chain
is a formal linear combination of k-simplices
.
The set of all k-chains forms a group and the sequence of these groups is called a chain complex
.
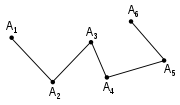
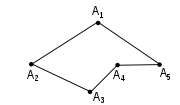The boundary of a chain is the linear combination of boundaries of the simplices in the chain. The boundary of a k-chain is a (k−1)-chain. Note that the boundary of a simplex is not a simplex, but a chain with coefficients 1 or −1 – thus chains are the closure of simplices under the boundary operator.
Example 1: The boundary of a path
is the formal difference of its endpoints: it is a telescoping sum. To illustrate, if the 1-chain
is a path from point 
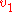to point 
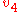, where
,
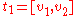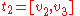and
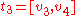are its constituent 1-simplices, then
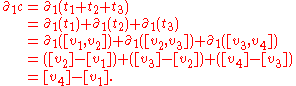
Example 2: The boundary of the triangle is a formal sum of its edges with signs arranged to make the traversal of the boundary counterclockwise.
A chain is called a cycle when its boundary is zero. A chain that is the boundary of another chain is called a boundary. Boundaries are cycles,
so chains form a chain complex
, whose homology groups (cycles modulo boundaries) are called simplicial homology
groups.
Example 3: A 0-cycle is a linear combination of points such that the sum of all the coefficients is 0. Thus, the 0-homology group measures the number of path connected components of the space.
Example 4: The plane punctured at the origin has nontrivial 1-homology group since the unit circle is a cycle, but not a boundary.
In differential geometry, the duality between the boundary operator on chains and the exterior derivative
is expressed by the general Stokes' theorem
.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a simplicial k-chain
is a formal linear combination of k-simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
.
Integration on chains
Integration is defined on chains by taking the linear combination of integrals over the simplices in the chain with coefficients typically integers.The set of all k-chains forms a group and the sequence of these groups is called a chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
.
Boundary operator on chains
Example 1: The boundary of a path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
is the formal difference of its endpoints: it is a telescoping sum. To illustrate, if the 1-chain
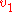is a path from point to point 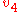, where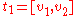, 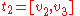and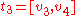 are its constituent 1-simplices, then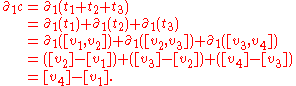Example 2: The boundary of the triangle is a formal sum of its edges with signs arranged to make the traversal of the boundary counterclockwise.
A chain is called a cycle when its boundary is zero. A chain that is the boundary of another chain is called a boundary. Boundaries are cycles,
so chains form a chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
, whose homology groups (cycles modulo boundaries) are called simplicial homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
groups.
Example 3: A 0-cycle is a linear combination of points such that the sum of all the coefficients is 0. Thus, the 0-homology group measures the number of path connected components of the space.
Example 4: The plane punctured at the origin has nontrivial 1-homology group since the unit circle is a cycle, but not a boundary.
In differential geometry, the duality between the boundary operator on chains and the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
is expressed by the general Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
.