Mathieu transformation
Encyclopedia
The Mathieu transformations make up a subgroup of canonical transformation
s preserving the differential form
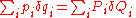
The transformation is named after the French mathematician Émile Léonard Mathieu
.
, there should exist at least one relation
between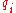
and 
only (without any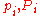 
involved).
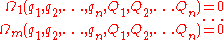
where
. When 
a Mathieu transformation becomes a Lagrange point transformation.
Canonical transformation
In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates → that preserves the form of Hamilton's equations , although it...
s preserving the differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
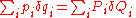
The transformation is named after the French mathematician Émile Léonard Mathieu
Émile Léonard Mathieu
Émile Léonard Mathieu was a French mathematician. He is most famous for his work in group theory and mathematical physics. He has given his name to the Mathieu functions, Mathieu groups and Mathieu transformation...
.
Details
In order to have this invarianceInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
, there should exist at least one relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
between
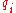and only (without any 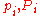involved).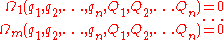where
. When a Mathieu transformation becomes a Lagrange point transformation.