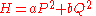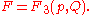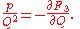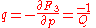Generating function (physics)
Encyclopedia
Generating functions which arise in Hamiltonian mechanics
are quite different from generating functions in mathematics. In the case of physics, generating functions act as a bridge between two sets of canonical variables when performing canonical transformation
.
Hamiltonian, which is
So, as an example, if one were given the Hamiltonian
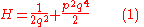
(where p is generalized momentum, and q is the generalized coordinate.)
a good canonical transformation to choose would be
This turns the Hamiltonian into
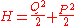
which is in the form of the harmonic oscillator Hamiltonian.
The generating function, F, for this transformation is of the 3rd kind,
To find F explicitly, use the equation for its derivative (from the table above),
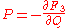
and substitute the expression for P from equation (2), expressed in terms of p and Q:
Integrating this with respect to Q results in an equation for the generating function of the transformation given by equation (2):
|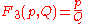
|}
To confirm that this is the correct generating function, verify that it matches (2):
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
are quite different from generating functions in mathematics. In the case of physics, generating functions act as a bridge between two sets of canonical variables when performing canonical transformation
Canonical transformation
In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates → that preserves the form of Hamilton's equations , although it...
.
Details
There are four basic generating functions, summarized by the following table.| Generating Function | Its Derivatives |
|---|---|
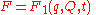 |
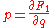 and and 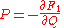 |
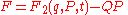 |
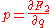 and and 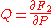 |
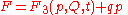 |
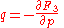 and and 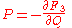 |
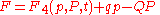 |
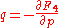 and and 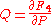 |
Example
Sometimes one can turn a given Hamiltonian into one that looks a bit more like the harmonic oscillatorHarmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
Hamiltonian, which is
So, as an example, if one were given the Hamiltonian
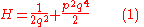
(where p is generalized momentum, and q is the generalized coordinate.)
a good canonical transformation to choose would be
This turns the Hamiltonian into
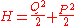
which is in the form of the harmonic oscillator Hamiltonian.
The generating function, F, for this transformation is of the 3rd kind,
To find F explicitly, use the equation for its derivative (from the table above),
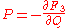
and substitute the expression for P from equation (2), expressed in terms of p and Q:
Integrating this with respect to Q results in an equation for the generating function of the transformation given by equation (2):
-
- {|cellpadding="2" style="border:2px solid #ccccff"
|
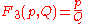
|}
To confirm that this is the correct generating function, verify that it matches (2):