
Smith normal form
Encyclopedia
In mathematics, the Smith normal form is a normal form
that can be defined for any matrix (not necessarily square) with entries in a principal ideal domain
(PID). The Smith normal form of a matrix is diagonal
, and can be obtained from the original matrix by multiplying on the left and right by invertible square matrices. In particular, the integers are a PID, so one can always calculate the Smith normal form of an integer matrix. The Smith normal form is very useful for working with finitely generated modules over a PID, and in particular for deducing the structure of a quotient of a free module
.
R. There exist invertible and
and  -matrices S, T so that the product S A T is
-matrices S, T so that the product S A T is
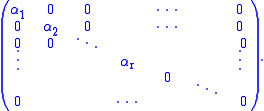
and the diagonal elements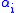 satisfy
satisfy 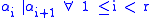 . This is the Smith normal form of the matrix A. The elements
. This is the Smith normal form of the matrix A. The elements 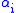 are unique up to
are unique up to
multiplication by a unit
and are called the elementary divisors, invariants, or invariant factors.
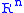 (the free R-module
(the free R-module
of rank n) onto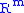 (the free R-module
(the free R-module
of rank m), there are isomorphisms and
and 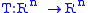 such that
such that  has the simple form of a diagonal matrix
has the simple form of a diagonal matrix
. The matrices S and T can be found by starting out with identity matrices of the appropriate size, and modifying S each time a row operation is performed on A in the algorithm by the same row operation, and similarly modifying T for each column operation performed. Since row operations are left-multiplications and column operations are right-multiplications, this preserves the invariant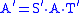 where
where 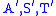 denote current values and A denotes the original matrix; eventually the matrices in this invariant become diagonal. Only invertible row and column operations are performed, which ensures that S and T remain invertible matrices.
denote current values and A denotes the original matrix; eventually the matrices in this invariant become diagonal. Only invertible row and column operations are performed, which ensures that S and T remain invertible matrices.
For a in R \ {0}, write δ(a) for the number of prime factors of a (these exist and are unique since any PID is also a unique factorization domain
). In particular, R is also a Bézout domain
, so it is a gcd domain
and the gcd of any two elements satisfies a Bézout's identity
.
To put a matrix into Smith normal form, one can repeatedly apply the following, where t loops from 1 to m.
We wish to have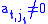 ; if this is the case this step is complete, otherwise there is by assumption some k with
; if this is the case this step is complete, otherwise there is by assumption some k with  , and we can exchange rows
, and we can exchange rows  and k, thereby obtaining
and k, thereby obtaining 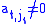 .
.
Our chosen pivot is now at position (t, jt).
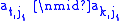 , then, letting
, then, letting  , we know by the Bézout property that there exist σ, τ in R such that
, we know by the Bézout property that there exist σ, τ in R such that

By left-multiplication with an appropriate invertible matrix L, it can be achieved that row t of the matrix product is the sum of σ times the original row t and τ times the original row k, that row k of the product is another linear combination of those original rows, and that all other rows are unchanged. Explicitly, if σ and τ satisfy the above equation, then for and
and 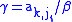 (which divisions are possible by the definition of β) one has
(which divisions are possible by the definition of β) one has

so that the matrix
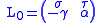
is invertible, with inverse
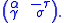
Now L can be obtained by fitting into rows and columns t and k of the identity matrix. By construction the matrix obtained after left-multiplying by L has entry β at position (t,jt) (and due to our choice of α and γ it also has an entry 0 at position (k,jt), which is useful though not essential for the algorithm). This new entry β divides the entry
into rows and columns t and k of the identity matrix. By construction the matrix obtained after left-multiplying by L has entry β at position (t,jt) (and due to our choice of α and γ it also has an entry 0 at position (k,jt), which is useful though not essential for the algorithm). This new entry β divides the entry  that was there before, and so in particular
that was there before, and so in particular 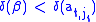 ; therefore repeating these steps must eventually terminate. One ends up with a matrix having an entry at position (t,jt) that divides all entries in column jt.
; therefore repeating these steps must eventually terminate. One ends up with a matrix having an entry at position (t,jt) that divides all entries in column jt.
However, notice that the ideals
generated by the elements at position (t,jt) form an ascending chain
, because entries from a later step always divide entries from a previous step. Therefore, since R is a Noetherian ring
(it is a PID
), the ideals eventually become stationary and do not change. This means that at some stage after Step II has been applied, the entry at (t,jt) will divide all nonzero row or column entries before applying any more steps in Step II. Then we can eliminate entries in the row or column with nonzero entries while preserving the zeros in the already-zero row or column. At this point, only the block of A to the lower right of (t,jt) needs to be diagonalized, and conceptually the algorithm can be applied recursively, treating this block as a separate matrix. In other words, we can increment t by one and go back to Step I.
 -matrix with column indices
-matrix with column indices  where
where 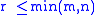 . The matrix entries
. The matrix entries 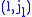 are non-zero, and every other entry is zero.
are non-zero, and every other entry is zero.
Now we can move the null columns of this matrix to the right, so that the nonzero entries are on positions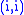 for
for 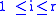 . For short, set
. For short, set  for the element at position
for the element at position 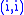 .
.
The condition of divisibility of diagonal entries might not be satisfied. For any index for which
for which 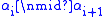 , one can repair this shortcoming by operations on rows and columns
, one can repair this shortcoming by operations on rows and columns  and
and  only: first add column
only: first add column  to column
to column 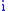 to get an entry
to get an entry 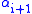 in column i without disturbing the entry
in column i without disturbing the entry 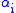 at position
at position 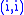 , and then apply a row operation to make the entry at position
, and then apply a row operation to make the entry at position 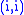 equal to
equal to  as in Step II; finally proceed as in Step III to make the matrix diagonal again. Since the new entry at position
as in Step II; finally proceed as in Step III to make the matrix diagonal again. Since the new entry at position 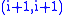 is a linear combination of the original
is a linear combination of the original 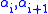 , it is divisible by β.
, it is divisible by β.
The value does not change by the above operation (it is δ of the determinant of the upper
does not change by the above operation (it is δ of the determinant of the upper  submatrix), whence that operation does diminish (by moving prime factors to the right) the value of
submatrix), whence that operation does diminish (by moving prime factors to the right) the value of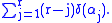
So after finitely many applications of this operation no further application is possible, which means that we have obtained as desired.
as desired.
Since all row and column manipulations involved in the process are invertible, this shows that there exist invertible and
and  -matrices S, T so that the product S A T satisfies the definition of a Smith normal form. In particular, this shows that the Smith normal form exists, which was assumed without proof in the definition.
-matrices S, T so that the product S A T satisfies the definition of a Smith normal form. In particular, this shows that the Smith normal form exists, which was assumed without proof in the definition.
of a chain complex
when the chain modules of the chain complex are finitely generated
. For instance, in topology
, it can be used to compute the homology of a simplicial complex
or CW complex
over the integers, because the boundary maps in such a complex are just integer matrices. It can also be used to prove the well known structure theorem for finitely generated modules over a principal ideal domain
.
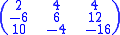
The following matrices are the intermediate steps as the algorithm is applied to the above matrix.
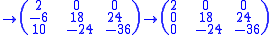


So the Smith normal form is
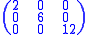
and the elementary divisors are 2, 6 and 12.
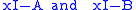 have the same Smith normal form.
have the same Smith normal form.
For example, with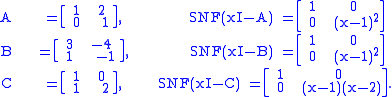
A and B are similar because the Smith normal form of their characteristic matrices match, but are not similar to C because the Smith normal form of the characteristic matrices do not match.
Canonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
that can be defined for any matrix (not necessarily square) with entries in a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
(PID). The Smith normal form of a matrix is diagonal
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
, and can be obtained from the original matrix by multiplying on the left and right by invertible square matrices. In particular, the integers are a PID, so one can always calculate the Smith normal form of an integer matrix. The Smith normal form is very useful for working with finitely generated modules over a PID, and in particular for deducing the structure of a quotient of a free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
.
Definition
Let A be a nonzero m×n matrix over a principal ideal domainPrincipal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
R. There exist invertible
 and
and  -matrices S, T so that the product S A T is
-matrices S, T so that the product S A T is
and the diagonal elements
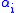 satisfy
satisfy 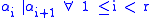 . This is the Smith normal form of the matrix A. The elements
. This is the Smith normal form of the matrix A. The elements 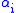 are unique up to
are unique up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
multiplication by a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
and are called the elementary divisors, invariants, or invariant factors.
Algorithm
Our first goal will be to find invertible square matrices S and T such that the product S A T is diagonal. This is the hardest part of the algorithm and once we have achieved diagonality it becomes relatively easy to put the matrix in Smith normal form. Phrased more abstractly, the goal is to show that, thinking of A as a map from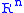 (the free R-module
(the free R-moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
of rank n) onto
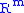 (the free R-module
(the free R-moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
of rank m), there are isomorphisms
 and
and 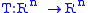 such that
such that  has the simple form of a diagonal matrix
has the simple form of a diagonal matrixDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. The matrices S and T can be found by starting out with identity matrices of the appropriate size, and modifying S each time a row operation is performed on A in the algorithm by the same row operation, and similarly modifying T for each column operation performed. Since row operations are left-multiplications and column operations are right-multiplications, this preserves the invariant
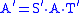 where
where 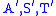 denote current values and A denotes the original matrix; eventually the matrices in this invariant become diagonal. Only invertible row and column operations are performed, which ensures that S and T remain invertible matrices.
denote current values and A denotes the original matrix; eventually the matrices in this invariant become diagonal. Only invertible row and column operations are performed, which ensures that S and T remain invertible matrices.For a in R \ {0}, write δ(a) for the number of prime factors of a (these exist and are unique since any PID is also a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
). In particular, R is also a Bézout domain
Bézout domain
In mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
, so it is a gcd domain
GCD domain
In mathematics, a GCD domain is an integral domain R with the property that any two non-zero elements have a greatest common divisor . Equivalently, any two non-zero elements of R have a least common multiple ....
and the gcd of any two elements satisfies a Bézout's identity
Bézout's identity
In number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
.
To put a matrix into Smith normal form, one can repeatedly apply the following, where t loops from 1 to m.
Step I : Choosing a pivot
Choose jt to be the smallest column index of A with a non-zero entry, starting the search at column index jt-1+1 if t > 1.We wish to have
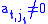 ; if this is the case this step is complete, otherwise there is by assumption some k with
; if this is the case this step is complete, otherwise there is by assumption some k with  , and we can exchange rows
, and we can exchange rows  and k, thereby obtaining
and k, thereby obtaining 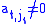 .
.Our chosen pivot is now at position (t, jt).
Step II : Improving the pivot
If there is an entry at position (k,jt) such that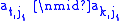 , then, letting
, then, letting  , we know by the Bézout property that there exist σ, τ in R such that
, we know by the Bézout property that there exist σ, τ in R such that
By left-multiplication with an appropriate invertible matrix L, it can be achieved that row t of the matrix product is the sum of σ times the original row t and τ times the original row k, that row k of the product is another linear combination of those original rows, and that all other rows are unchanged. Explicitly, if σ and τ satisfy the above equation, then for
 and
and 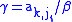 (which divisions are possible by the definition of β) one has
(which divisions are possible by the definition of β) one has
so that the matrix
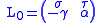
is invertible, with inverse
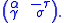
Now L can be obtained by fitting
 into rows and columns t and k of the identity matrix. By construction the matrix obtained after left-multiplying by L has entry β at position (t,jt) (and due to our choice of α and γ it also has an entry 0 at position (k,jt), which is useful though not essential for the algorithm). This new entry β divides the entry
into rows and columns t and k of the identity matrix. By construction the matrix obtained after left-multiplying by L has entry β at position (t,jt) (and due to our choice of α and γ it also has an entry 0 at position (k,jt), which is useful though not essential for the algorithm). This new entry β divides the entry  that was there before, and so in particular
that was there before, and so in particular 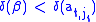 ; therefore repeating these steps must eventually terminate. One ends up with a matrix having an entry at position (t,jt) that divides all entries in column jt.
; therefore repeating these steps must eventually terminate. One ends up with a matrix having an entry at position (t,jt) that divides all entries in column jt.Step III : Eliminating entries
Finally, adding appropriate multiples of row t, it can be achieved that all entries in column jt except for that at position (t,jt) are zero. This can be achieved by left-multiplication with an appropriate matrix. However, to make the matrix fully diagonal we need to eliminate nonzero entries on the row of position (t,jt) as well. This can be achieved by repeating the steps in Step II for columns instead of rows, and using multiplication on the right. In general this will result in the zero entries from the prior application of Step III becoming nonzero again.However, notice that the ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by the elements at position (t,jt) form an ascending chain
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
, because entries from a later step always divide entries from a previous step. Therefore, since R is a Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
(it is a PID
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
), the ideals eventually become stationary and do not change. This means that at some stage after Step II has been applied, the entry at (t,jt) will divide all nonzero row or column entries before applying any more steps in Step II. Then we can eliminate entries in the row or column with nonzero entries while preserving the zeros in the already-zero row or column. At this point, only the block of A to the lower right of (t,jt) needs to be diagonalized, and conceptually the algorithm can be applied recursively, treating this block as a separate matrix. In other words, we can increment t by one and go back to Step I.
Final step
Applying the steps described above to the remaining non-zero columns of the resulting matrix (if any), we get an -matrix with column indices
-matrix with column indices  where
where 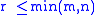 . The matrix entries
. The matrix entries 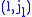 are non-zero, and every other entry is zero.
are non-zero, and every other entry is zero.Now we can move the null columns of this matrix to the right, so that the nonzero entries are on positions
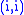 for
for 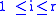 . For short, set
. For short, set  for the element at position
for the element at position 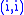 .
.The condition of divisibility of diagonal entries might not be satisfied. For any index
 for which
for which 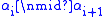 , one can repair this shortcoming by operations on rows and columns
, one can repair this shortcoming by operations on rows and columns  and
and  only: first add column
only: first add column  to column
to column 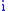 to get an entry
to get an entry 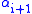 in column i without disturbing the entry
in column i without disturbing the entry 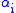 at position
at position 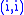 , and then apply a row operation to make the entry at position
, and then apply a row operation to make the entry at position 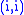 equal to
equal to  as in Step II; finally proceed as in Step III to make the matrix diagonal again. Since the new entry at position
as in Step II; finally proceed as in Step III to make the matrix diagonal again. Since the new entry at position 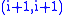 is a linear combination of the original
is a linear combination of the original 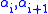 , it is divisible by β.
, it is divisible by β.The value
 does not change by the above operation (it is δ of the determinant of the upper
does not change by the above operation (it is δ of the determinant of the upper  submatrix), whence that operation does diminish (by moving prime factors to the right) the value of
submatrix), whence that operation does diminish (by moving prime factors to the right) the value of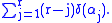
So after finitely many applications of this operation no further application is possible, which means that we have obtained
 as desired.
as desired.Since all row and column manipulations involved in the process are invertible, this shows that there exist invertible
 and
and  -matrices S, T so that the product S A T satisfies the definition of a Smith normal form. In particular, this shows that the Smith normal form exists, which was assumed without proof in the definition.
-matrices S, T so that the product S A T satisfies the definition of a Smith normal form. In particular, this shows that the Smith normal form exists, which was assumed without proof in the definition.Applications
The Smith normal form is useful for computing the homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of a chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
when the chain modules of the chain complex are finitely generated
Finitely generated
In mathematics, finitely generated may refer to:* Finitely generated group* Finitely generated monoid* Finitely generated abelian group* Finitely generated module* Finitely generated ideal* Finitely generated algebra* Finitely generated space...
. For instance, in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, it can be used to compute the homology of a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
or CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
over the integers, because the boundary maps in such a complex are just integer matrices. It can also be used to prove the well known structure theorem for finitely generated modules over a principal ideal domain
Structure theorem for finitely generated modules over a principal ideal domain
In mathematics, in the field of abstract algebra, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in...
.
Example
As an example, we will find the Smith normal form of the following matrix over the integers.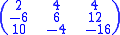
The following matrices are the intermediate steps as the algorithm is applied to the above matrix.
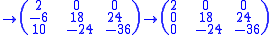


So the Smith normal form is
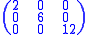
and the elementary divisors are 2, 6 and 12.
Similarity
The Smith normal form can be used to determine whether or not matrices with entries over a common field are similar. Specifically two matrices A and B are similar if and only if the characteristic matrices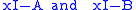 have the same Smith normal form.
have the same Smith normal form.For example, with
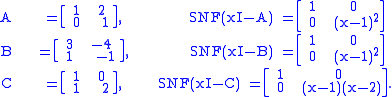
A and B are similar because the Smith normal form of their characteristic matrices match, but are not similar to C because the Smith normal form of the characteristic matrices do not match.
See also
- Canonical formCanonical formGenerally, in mathematics, a canonical form of an object is a standard way of presenting that object....
- Henry John Stephen SmithHenry John Stephen SmithHenry John Stephen Smith was a mathematician remembered for his work in elementary divisors, quadratic forms, and Smith–Minkowski–Siegel mass formula in number theory...
(1826 – 1883), whose name is attached to the Smith normal form
External links
- Thomas Heye's GFDL Smith normal form article at PlanetMath
- GFDL Example of Smith normal form at PlanetMath

