
Frobenius normal form
Encyclopedia
In linear algebra
, the Frobenius normal form, Turner binormal projective form or rational canonical form of a square matrix A is a canonical form
for matrices
that reflects the structure of the minimal polynomial of A and provides a means of detecting whether another matrix B is similar to A without extending
the base field
F.
For example, let F be the field R of real number
s, consider the following matrix A, over R:

The characteristic polynomial of A is x6 + 6x4 + 12x2 + 8 = (x2 + 2)3 = p(x). The minimal polynomial
of this matrix is x2 + 2.
We will then have one block in the Frobenius normal form as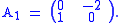
The characteristic polynomial of A1 is indeed x2 + 2.
Since p factors into solely terms of the form x2 + 2, we expect the other two blocks comprising the normal form of the matrix to be identical to A1. So, we can simply write down the Frobenius normal form:
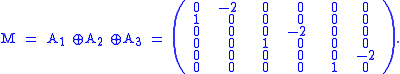
The characteristic and minimal polynomials of M are the same as those of A, which we would expect, since M can be obtained via a similarity transformation P−1AP = M, and determinant
s are similarity invariant. For this matrix A, P is
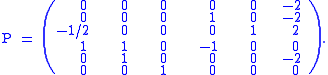
V over F. Given a polynomial p(x) ∈ F[x], there is associated to it a companion matrix C whose characteristic polynomial
is p(x).
Theorem: Let V be a finite-dimensional vector space over a field F, and A a square matrix over F. Then V (viewed as an F[x]-module
with the action of x given by A and extending by linearity) satisfies the F[x]-module isomorphism
where the ai(x) ∈ F[x] may be taken to be non-unit
s, unique as monic polynomials, and can be arranged to satisfy the relation
where "a | b" is notation for "a divides b".
Sketch of Proof: Apply the structure theorem for finitely generated modules over a principal ideal domain
to V, viewing it as an F[x]-module. Note that any free F[x]-module is infinite-dimensional over F, so that the resulting direct sum decomposition has no free
part since V is finite-dimensional. The uniqueness of the invariant factors requires a separate proof that they are determined up to units; then the monic condition ensures that they are uniquely determined. The proof of this latter part is omitted. See [DF] for details.
Given an arbitrary square matrix, the elementary divisors
used in the construction of the Jordan normal form
do not exist over F[x], so the invariant factors ai(x) as given above must be used instead. These correspond to factors of the minimal polynomial m(x) = an(x), which (by the Cayley–Hamilton theorem
) itself divides the characteristic polynomial p(x) and in fact has the same roots as p(x), not counting multiplicities. Note in particular that the Theorem asserts that the invariant factors have coefficients in F.
As each invariant factor ai(x) is a polynomial in F[x], we may associate a corresponding block matrix
Ci which is the companion matrix to ai(x). In particular, each such Ci has its entries in the field F.
Taking the matrix direct sum of these blocks over all the invariant factors yields the rational canonical form of A. Where the minimal polynomial is identical to the characteristic polynomial, the Frobenius normal form is the companion matrix of the characteristic polynomial. As the rational canonical form is uniquely determined by the unique invariant factors associated to A, and these invariant factors are independent of basis, it follows that two square matrices A and B are similar if and only if they have the same rational canonical form.
(if A is diagonalizable) or more generally the Jordan normal form
(if the characteristic polynomial splits into linear factors). For instance, the Frobenius normal form of a diagonal matrix with distinct diagonal entries is just the companion matrix of its characteristic polynomial.
There is another way to define a normal form, that like the Frobenius normal form is always defined over the same field F as A, but that does reflect a possible factorization of the characteristic polynomial (or equivalently the minimal polynomial) into irreducible factors over F, and which reduces to the Jordan normal form in case this factorization only contain linear factors (corresponding to eigenvalues). This form is sometimes called the generalized Jordan normal form, or primary rational canonical form. It is based on the fact that the vector space can be canonically decomposed into a direct sum of stable subspaces corresponding to the distinct irreducible factors P of the characteristic polynomial (as stated by the lemme des noyaux), where the characteristic polynomial of each summand is a power of the corresponding P. These summands can be further decomposed, non-canonically, as a direct sum of cyclic F[x]-modules (like is done for the Frobenius normal form above), where the characteristic polynomial of each summand is still a (generally smaller) power of P. The primary rational canonical form is a block diagonal matrix corresponding to such a decomposition into cyclic modules, with a particular form called generalized Jordan block in the diagonal blocks, corresponding to a particular choice of a basis for the cyclic modules. This generalized Jordan block is itself a block matrix
of the form
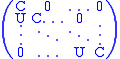
where C is the companion matrix of the irreducible polynomial , and is a matrix whose sole nonzero entry is a 1 in the upper right hand corner. For the case of a linear irreducible factor , these blocks are reduced to single entries and and, one finds a (transposed) Jordan block. In any generalized Jordan block, all enrties immediately below the main diagonal are 1. A basis of the cyclic module giving rise to this form is obtained by choosing a generating vector (one that is not annihilated by where the minimal polynomial of the cyclic module is ), and taking as basis
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the Frobenius normal form, Turner binormal projective form or rational canonical form of a square matrix A is a canonical form
Canonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
for matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that reflects the structure of the minimal polynomial of A and provides a means of detecting whether another matrix B is similar to A without extending
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
the base field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F.
Motivating example
The Frobenius normal form M of a matrix A with entries in a field F can be obtained from it by means of a similarity transformation. What this implies is that there is an invertible matrix P with entries in F for which P−1AP = M. Every matrix can be transformed by a similarity transformation to its Frobenius normal form.For example, let F be the field R of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, consider the following matrix A, over R:

The characteristic polynomial of A is x6 + 6x4 + 12x2 + 8 = (x2 + 2)3 = p(x). The minimal polynomial
Minimal polynomial (linear algebra)
In linear algebra, the minimal polynomial of an n-by-n matrix A over a field F is the monic polynomial P over F of least degree such that P=0...
of this matrix is x2 + 2.
We will then have one block in the Frobenius normal form as
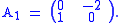
The characteristic polynomial of A1 is indeed x2 + 2.
Since p factors into solely terms of the form x2 + 2, we expect the other two blocks comprising the normal form of the matrix to be identical to A1. So, we can simply write down the Frobenius normal form:
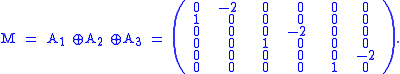
The characteristic and minimal polynomials of M are the same as those of A, which we would expect, since M can be obtained via a similarity transformation P−1AP = M, and determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s are similarity invariant. For this matrix A, P is
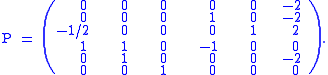
General case and theory
Fix a base field F and a finite-dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over F. Given a polynomial p(x) ∈ F[x], there is associated to it a companion matrix C whose characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
is p(x).
Theorem: Let V be a finite-dimensional vector space over a field F, and A a square matrix over F. Then V (viewed as an F[x]-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
with the action of x given by A and extending by linearity) satisfies the F[x]-module isomorphism
- V ≅ F[x]/(a1(x)) ⊕ … ⊕ F[x]/(an(x))
where the ai(x) ∈ F[x] may be taken to be non-unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
s, unique as monic polynomials, and can be arranged to satisfy the relation
- a1(x) | … | an(x)
where "a | b" is notation for "a divides b".
Sketch of Proof: Apply the structure theorem for finitely generated modules over a principal ideal domain
Structure theorem for finitely generated modules over a principal ideal domain
In mathematics, in the field of abstract algebra, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in...
to V, viewing it as an F[x]-module. Note that any free F[x]-module is infinite-dimensional over F, so that the resulting direct sum decomposition has no free
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
part since V is finite-dimensional. The uniqueness of the invariant factors requires a separate proof that they are determined up to units; then the monic condition ensures that they are uniquely determined. The proof of this latter part is omitted. See [DF] for details.
Given an arbitrary square matrix, the elementary divisors
Elementary divisors
In algebra, the elementary divisors of a module over a principal ideal domain occur in one form of the structure theorem for finitely generated modules over a principal ideal domain....
used in the construction of the Jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
do not exist over F[x], so the invariant factors ai(x) as given above must be used instead. These correspond to factors of the minimal polynomial m(x) = an(x), which (by the Cayley–Hamilton theorem
Cayley–Hamilton theorem
In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
) itself divides the characteristic polynomial p(x) and in fact has the same roots as p(x), not counting multiplicities. Note in particular that the Theorem asserts that the invariant factors have coefficients in F.
As each invariant factor ai(x) is a polynomial in F[x], we may associate a corresponding block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
Ci which is the companion matrix to ai(x). In particular, each such Ci has its entries in the field F.
Taking the matrix direct sum of these blocks over all the invariant factors yields the rational canonical form of A. Where the minimal polynomial is identical to the characteristic polynomial, the Frobenius normal form is the companion matrix of the characteristic polynomial. As the rational canonical form is uniquely determined by the unique invariant factors associated to A, and these invariant factors are independent of basis, it follows that two square matrices A and B are similar if and only if they have the same rational canonical form.
A rational normal form generalizing the Jordan normal form
The Frobenius normal form does not reflect any form of factorization of the characteristic polynomial, even if it does exist over the ground field F. This implies that it is invariant when F is replaced by a different field (as long as it contains the entries of the original matrix A). On the other hand this makes the Frobenius normal form rather different than other normal forms that do depend on factoring the characteristic polynomial, notably the diagonal formDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
(if A is diagonalizable) or more generally the Jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
(if the characteristic polynomial splits into linear factors). For instance, the Frobenius normal form of a diagonal matrix with distinct diagonal entries is just the companion matrix of its characteristic polynomial.
There is another way to define a normal form, that like the Frobenius normal form is always defined over the same field F as A, but that does reflect a possible factorization of the characteristic polynomial (or equivalently the minimal polynomial) into irreducible factors over F, and which reduces to the Jordan normal form in case this factorization only contain linear factors (corresponding to eigenvalues). This form is sometimes called the generalized Jordan normal form, or primary rational canonical form. It is based on the fact that the vector space can be canonically decomposed into a direct sum of stable subspaces corresponding to the distinct irreducible factors P of the characteristic polynomial (as stated by the lemme des noyaux), where the characteristic polynomial of each summand is a power of the corresponding P. These summands can be further decomposed, non-canonically, as a direct sum of cyclic F[x]-modules (like is done for the Frobenius normal form above), where the characteristic polynomial of each summand is still a (generally smaller) power of P. The primary rational canonical form is a block diagonal matrix corresponding to such a decomposition into cyclic modules, with a particular form called generalized Jordan block in the diagonal blocks, corresponding to a particular choice of a basis for the cyclic modules. This generalized Jordan block is itself a block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
of the form
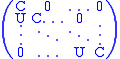
where C is the companion matrix of the irreducible polynomial , and is a matrix whose sole nonzero entry is a 1 in the upper right hand corner. For the case of a linear irreducible factor , these blocks are reduced to single entries and and, one finds a (transposed) Jordan block. In any generalized Jordan block, all enrties immediately below the main diagonal are 1. A basis of the cyclic module giving rise to this form is obtained by choosing a generating vector (one that is not annihilated by where the minimal polynomial of the cyclic module is ), and taking as basis


