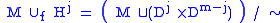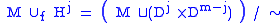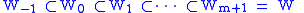Handle decomposition
Encyclopedia
In mathematics
, a handle decomposition of an m-manifold
M is a union

where each is obtained from
is obtained from 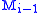
by the attaching of -handles. A handle decomposition is to a manifold what a CW-decomposition
-handles. A handle decomposition is to a manifold what a CW-decomposition
is to a topological space—in many regards the purpose of a handle decomposition is to have a language analogous to CW-complexes, but adapted to the world of smooth manifolds. Thus an i-handle is the smooth analogue of an i-cell. Handle decompositions of manifolds arise naturally via Morse theory
. The modification of handle structures is closely linked to Cerf theory
.

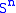 from the eyes of this decomposition -- in particular the smooth structure near the 0-cell depends on the behavior of the characteristic map
from the eyes of this decomposition -- in particular the smooth structure near the 0-cell depends on the behavior of the characteristic map  in a neighbourhood of
in a neighbourhood of 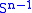 .
.
The problem with CW-decompositions is that the attaching maps for cells do not live in the world of smooth maps between manifolds. The germinal insight to correct this defect is the tubular neighbourhood theorem
. Given a point p in a manifold M, its closed tubular neighbourhood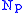 is diffeomorphic to
is diffeomorphic to 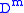 , thus we have decomposed M into the disjoint union of
, thus we have decomposed M into the disjoint union of 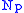 and
and 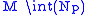 glued along their common boundary. The vital issue here is that the gluing map is a diffeomorphism. Similarly, take a smooth embedded arc in
glued along their common boundary. The vital issue here is that the gluing map is a diffeomorphism. Similarly, take a smooth embedded arc in 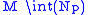 , its tubular neighbourhood is diffeomorphic to
, its tubular neighbourhood is diffeomorphic to 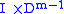 . This allows us to write
. This allows us to write  as the union of three manifolds, glued along parts of their boundaries: 1)
as the union of three manifolds, glued along parts of their boundaries: 1)  2)
2) 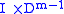 and 3) the complement of the open tubular neighbourhood of the arc in
and 3) the complement of the open tubular neighbourhood of the arc in 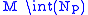 . Notice all the gluing maps are smooth maps—in particular when we glue
. Notice all the gluing maps are smooth maps—in particular when we glue 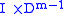 to
to 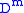 the equivalence relation is generated by the embedding of
the equivalence relation is generated by the embedding of  in
in 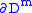 , which is smooth by the tubular neighbourhood theorem
, which is smooth by the tubular neighbourhood theorem
.
Handle decompositions are an invention of Stephen Smale. In his original formulation, the process of attaching a j-handle to an m-manifold M assumes that one has a smooth embedding of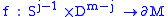 . Let
. Let 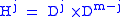 . The manifold
. The manifold 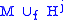 (in words, M union a j-handle along f ) refers to the disjoint union of
(in words, M union a j-handle along f ) refers to the disjoint union of  and
and 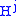 with the identification of
with the identification of  with its image in
with its image in  , i.e.:
, i.e.:
where the equivalence relation
 is generated by
is generated by 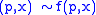 for all
for all 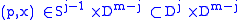 .
.
One says a manifold N is obtained from M by attaching j-handles, if M union finitely many j-handles is diffeomorphic to N. The definition of a handle decomposition is then as in the introduction. Thus, a manifold has a handle decomposition with only 0-handles if it is diffeomorphic to a disjoint union of balls. A connected manifold containing handles of only two types (ie: 0-handles and j-handles for some fixed j) is called a handlebody
.
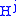
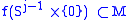 is known as the attaching sphere.
is known as the attaching sphere.
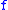 is sometimes called the framing of the attaching sphere, since it gives trivialization
is sometimes called the framing of the attaching sphere, since it gives trivialization
of its normal bundle
.
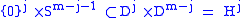 is the belt sphere of the handle
is the belt sphere of the handle 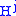 in
in  .
.
A manifold obtained by attaching g k-handles to the disc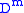 is an (m,k)-handlebody of genus g .
is an (m,k)-handlebody of genus g .
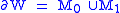 and an ascending union
and an ascending union
where M is m-dimensional, W is m+1-dimensional,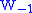 is diffeomorphic to
is diffeomorphic to 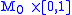 and
and 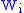 is obtained from
is obtained from 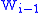 by the attachment of i-handles. Whereas handle decompositions are the analogue for manifolds what cell decompositions are to topological spaces, handle presentations of cobordisms are to manifolds with boundary what relative cell decompositions are for pairs of spaces.
by the attachment of i-handles. Whereas handle decompositions are the analogue for manifolds what cell decompositions are to topological spaces, handle presentations of cobordisms are to manifolds with boundary what relative cell decompositions are for pairs of spaces.
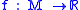 on a compact boundaryless manifold M, such that the critical points
on a compact boundaryless manifold M, such that the critical points
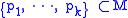 of f satisfy
of f satisfy  , and provided
, and provided
 ,
,
then for all j,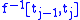 is diffeomorphic to
is diffeomorphic to 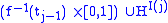 where I(j) is the index of the critical point
where I(j) is the index of the critical point 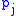 . The index I(j) refers to the dimension of the maximal subspace of the tangent space
. The index I(j) refers to the dimension of the maximal subspace of the tangent space  where the Hessian
where the Hessian
is negative definite.
Provided the indices satisfy this is a handle decomposition of M, moreover, every manifold has such Morse functions, so they have handle decompositions. Similarly, given a cobordism
this is a handle decomposition of M, moreover, every manifold has such Morse functions, so they have handle decompositions. Similarly, given a cobordism  with
with  and a function
and a function  which is Morse on the interior and constant on the boundary and satisfying the increasing index property, there is an induced handle presentation of the cobordism W.
which is Morse on the interior and constant on the boundary and satisfying the increasing index property, there is an induced handle presentation of the cobordism W.
When f is a Morse function on M, -f is also a Morse function. The corresponding handle decomposition / presentation is called the dual decomposition.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a handle decomposition of an m-manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M is a union

where each
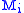 is obtained from
is obtained from 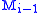
by the attaching of
 -handles. A handle decomposition is to a manifold what a CW-decomposition
-handles. A handle decomposition is to a manifold what a CW-decompositionCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
is to a topological space—in many regards the purpose of a handle decomposition is to have a language analogous to CW-complexes, but adapted to the world of smooth manifolds. Thus an i-handle is the smooth analogue of an i-cell. Handle decompositions of manifolds arise naturally via Morse theory
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
. The modification of handle structures is closely linked to Cerf theory
Cerf theory
In mathematics, at the junction of singularity theory and differential topology, Cerf theory is the study of families of smooth real-valued functionsf:M \to \mathbb R...
.

Motivation
Consider the standard CW-decomposition of the n-sphere, with one zero cell and a single n-cell. From the point of view of smooth manifolds, this is a degenerate decomposition of the sphere, as there is no natural way to see the smooth structure of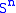 from the eyes of this decomposition -- in particular the smooth structure near the 0-cell depends on the behavior of the characteristic map
from the eyes of this decomposition -- in particular the smooth structure near the 0-cell depends on the behavior of the characteristic map  in a neighbourhood of
in a neighbourhood of 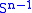 .
.The problem with CW-decompositions is that the attaching maps for cells do not live in the world of smooth maps between manifolds. The germinal insight to correct this defect is the tubular neighbourhood theorem
Tubular neighborhood
In mathematics, a tubular neighborhood of a submanifold of a smooth manifold is an open set around it resembling the normal bundle.The idea behind a tubular neighborhood can be explained in a simple example. Consider a smooth curve in the plane without self-intersections. On each point on the curve...
. Given a point p in a manifold M, its closed tubular neighbourhood
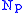 is diffeomorphic to
is diffeomorphic to 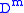 , thus we have decomposed M into the disjoint union of
, thus we have decomposed M into the disjoint union of 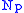 and
and 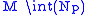 glued along their common boundary. The vital issue here is that the gluing map is a diffeomorphism. Similarly, take a smooth embedded arc in
glued along their common boundary. The vital issue here is that the gluing map is a diffeomorphism. Similarly, take a smooth embedded arc in 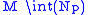 , its tubular neighbourhood is diffeomorphic to
, its tubular neighbourhood is diffeomorphic to 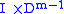 . This allows us to write
. This allows us to write  as the union of three manifolds, glued along parts of their boundaries: 1)
as the union of three manifolds, glued along parts of their boundaries: 1)  2)
2) 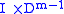 and 3) the complement of the open tubular neighbourhood of the arc in
and 3) the complement of the open tubular neighbourhood of the arc in 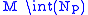 . Notice all the gluing maps are smooth maps—in particular when we glue
. Notice all the gluing maps are smooth maps—in particular when we glue 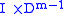 to
to 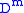 the equivalence relation is generated by the embedding of
the equivalence relation is generated by the embedding of  in
in 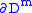 , which is smooth by the tubular neighbourhood theorem
, which is smooth by the tubular neighbourhood theoremTubular neighborhood
In mathematics, a tubular neighborhood of a submanifold of a smooth manifold is an open set around it resembling the normal bundle.The idea behind a tubular neighborhood can be explained in a simple example. Consider a smooth curve in the plane without self-intersections. On each point on the curve...
.
Handle decompositions are an invention of Stephen Smale. In his original formulation, the process of attaching a j-handle to an m-manifold M assumes that one has a smooth embedding of
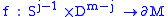 . Let
. Let 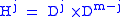 . The manifold
. The manifold 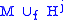 (in words, M union a j-handle along f ) refers to the disjoint union of
(in words, M union a j-handle along f ) refers to the disjoint union of  and
and 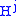 with the identification of
with the identification of  with its image in
with its image in  , i.e.:
, i.e.:where the equivalence relation
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
 is generated by
is generated by 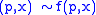 for all
for all 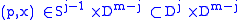 .
.One says a manifold N is obtained from M by attaching j-handles, if M union finitely many j-handles is diffeomorphic to N. The definition of a handle decomposition is then as in the introduction. Thus, a manifold has a handle decomposition with only 0-handles if it is diffeomorphic to a disjoint union of balls. A connected manifold containing handles of only two types (ie: 0-handles and j-handles for some fixed j) is called a handlebody
Handlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
.
Terminology
When forming M union a j-handle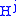
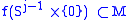 is known as the attaching sphere.
is known as the attaching sphere.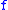 is sometimes called the framing of the attaching sphere, since it gives trivialization
is sometimes called the framing of the attaching sphere, since it gives trivializationVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
of its normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
.
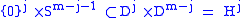 is the belt sphere of the handle
is the belt sphere of the handle 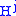 in
in  .
.A manifold obtained by attaching g k-handles to the disc
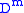 is an (m,k)-handlebody of genus g .
is an (m,k)-handlebody of genus g .Cobordism presentations
A handle presentation of a cobordism consists of a cobordism W where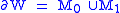 and an ascending union
and an ascending unionwhere M is m-dimensional, W is m+1-dimensional,
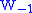 is diffeomorphic to
is diffeomorphic to 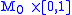 and
and 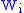 is obtained from
is obtained from 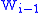 by the attachment of i-handles. Whereas handle decompositions are the analogue for manifolds what cell decompositions are to topological spaces, handle presentations of cobordisms are to manifolds with boundary what relative cell decompositions are for pairs of spaces.
by the attachment of i-handles. Whereas handle decompositions are the analogue for manifolds what cell decompositions are to topological spaces, handle presentations of cobordisms are to manifolds with boundary what relative cell decompositions are for pairs of spaces.Morse theoretic viewpoint
Given a Morse functionMorse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
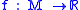 on a compact boundaryless manifold M, such that the critical points
on a compact boundaryless manifold M, such that the critical pointsCritical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
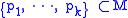 of f satisfy
of f satisfy  , and provided
, and provided ,
,then for all j,
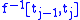 is diffeomorphic to
is diffeomorphic to 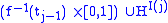 where I(j) is the index of the critical point
where I(j) is the index of the critical point 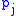 . The index I(j) refers to the dimension of the maximal subspace of the tangent space
. The index I(j) refers to the dimension of the maximal subspace of the tangent space  where the Hessian
where the HessianHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
is negative definite.
Provided the indices satisfy
 this is a handle decomposition of M, moreover, every manifold has such Morse functions, so they have handle decompositions. Similarly, given a cobordism
this is a handle decomposition of M, moreover, every manifold has such Morse functions, so they have handle decompositions. Similarly, given a cobordism  with
with  and a function
and a function  which is Morse on the interior and constant on the boundary and satisfying the increasing index property, there is an induced handle presentation of the cobordism W.
which is Morse on the interior and constant on the boundary and satisfying the increasing index property, there is an induced handle presentation of the cobordism W.When f is a Morse function on M, -f is also a Morse function. The corresponding handle decomposition / presentation is called the dual decomposition.
Some major theorems and observations
- A Heegaard splittingHeegaard splittingIn the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.-Definitions:...
of a closed, orientable 3-manifold is a decomposition of a 3-manifold into the union of two (3,1)-handlebodies along their common boundary, called the Heegaard splitting surface. Heegaard splittings arise for 3-manifolds in several natural ways: given a handle decomposition of a 3-manifold, the union of the 0 and 1-handles is a (3,1)-handlebody, and the union of the 3 and 2-handles is also a (3,1)-handlebody (from the point of view of the dual decomposition), thus a Heegaard splitting. If the 3-manifold has a triangulationTriangulation (topology)In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
T, there is an induced Heegaard splitting where the first (3,1)-handlebody is a regular neighbourhood of the 1-skeleton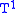 , and the other (3,1)-handlebody is a regular neighbourhood of the dual 1-skeletonPoincaré dualityIn mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
, and the other (3,1)-handlebody is a regular neighbourhood of the dual 1-skeletonPoincaré dualityIn mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
.
- When attaching two handles in succession
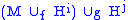 , it is possible to switch the order of attachment, provided
, it is possible to switch the order of attachment, provided  , i.e.: this manifold is diffeomorphic to a manifold of the form
, i.e.: this manifold is diffeomorphic to a manifold of the form  for suitable attaching maps.
for suitable attaching maps.
- The boundary of
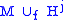 is diffeomorphic to
is diffeomorphic to  surgered along the framed sphere
surgered along the framed sphere 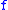 . This is the primary link between surgerySurgery theoryIn mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
. This is the primary link between surgerySurgery theoryIn mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
, handles and Morse functions.
- As a consequence, an m-manifold M is the boundary of an m+1-manifold W if and only if M can be obtained from
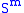 by surgery on a collection of framed links in
by surgery on a collection of framed links in 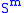 . For example, it's known that every 3-manifold bounds a 4-manifold (similarly oriented and spin 3-manifolds bound oriented and spin 4-manifolds respectively) due to René Thom's work on cobordismCobordismIn mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
. For example, it's known that every 3-manifold bounds a 4-manifold (similarly oriented and spin 3-manifolds bound oriented and spin 4-manifolds respectively) due to René Thom's work on cobordismCobordismIn mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
. Thus every 3-manifold can be obtained via surgery on framed links in the 3-sphere. In the oriented case, it's conventional to reduce this framed link to a framed embedding of a disjoint union of circles.
- The H-cobordism TheoremH-cobordismA cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...
is proven by simplifying handle decompositions of smooth manifolds.
See also
- Casson handleCasson handleIn 4-dimensional topology, a branch of mathematics, a Casson handle is a 4-dimensional topological 2-handle constructed by an infinite procedure. They are named for Andrew Casson, who introduced them in about 1973. They were originally called "flexible handles" by Casson himself, and introduced...
- Cobordism theory
- CW complexCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
- HandlebodyHandlebodyIn the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
- Kirby calculusKirby calculusIn mathematics, the Kirby calculus in geometric topology, named after Robion Kirby, is a method for modifying framed links in the 3-sphere using a finite set of moves, the Kirby moves...
- Manifold decompositionManifold decompositionIn topology, a branch of mathematics, a manifold M may be decomposed or split by writing M as a combination of smaller pieces. When doing so, one must specify both what those pieces are and how they are put together to form M....
General references
- A. Kosinksi, Differential Manifolds Vol 138 Pure and Applied Mathematics, Academic Press (1992).
- Robert Gompf and Andras Stipsicz, 4-Manifolds and Kirby Calculus, (1999) (Volume 20 in Graduate Studies in Mathematics), American Mathematical Society, Providence, RI ISBN 0-8218-0994-6