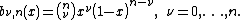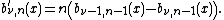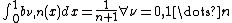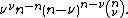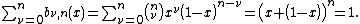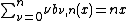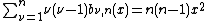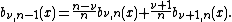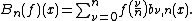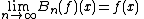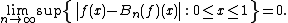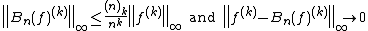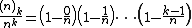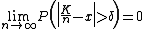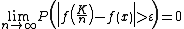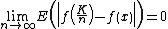Bernstein polynomial
Encyclopedia
In the mathematical
field of numerical analysis
, a Bernstein polynomial, named after Sergei Natanovich Bernstein
, is a polynomial
in the Bernstein form, that is a linear combination
of Bernstein basis polynomials.
A numerically stable
way to evaluate polynomials in Bernstein form is de Casteljau's algorithm
.
Polynomials in Bernstein form were first used by Bernstein in a constructive proof for the Stone–Weierstrass approximation theorem. With the advent of computer graphics, Bernstein polynomials, restricted to the interval x ∈ [0, 1], became important in the form of Bézier curve
s.
where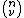 is a binomial coefficient
is a binomial coefficient
.
The Bernstein basis polynomials of degree n form a basis
for the vector space
Πn of polynomials of degree n.
A linear combination of Bernstein basis polynomials

is called a Bernstein polynomial or polynomial in Bernstein form of degree n. The coefficients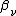 are called Bernstein coefficients or Bézier coefficients.
are called Bernstein coefficients or Bézier coefficients.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, a Bernstein polynomial, named after Sergei Natanovich Bernstein
Sergei Natanovich Bernstein
Sergei Natanovich Bernstein was a Russian and Soviet mathematician known for contributions to partial differential equations, differential geometry, probability theory, and approximation theory.-Partial differential equations:...
, is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in the Bernstein form, that is a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of Bernstein basis polynomials.
A numerically stable
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
way to evaluate polynomials in Bernstein form is de Casteljau's algorithm
De Casteljau's algorithm
In the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau...
.
Polynomials in Bernstein form were first used by Bernstein in a constructive proof for the Stone–Weierstrass approximation theorem. With the advent of computer graphics, Bernstein polynomials, restricted to the interval x ∈ [0, 1], became important in the form of Bézier curve
Bézier curve
A Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case....
s.
Definition
The n + 1 Bernstein basis polynomials of degree n are defined aswhere
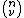 is a binomial coefficient
is a binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
.
The Bernstein basis polynomials of degree n form a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
Πn of polynomials of degree n.
A linear combination of Bernstein basis polynomials

is called a Bernstein polynomial or polynomial in Bernstein form of degree n. The coefficients
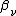 are called Bernstein coefficients or Bézier coefficients.
are called Bernstein coefficients or Bézier coefficients.Example
The first few Bernstein basis polynomials are:-
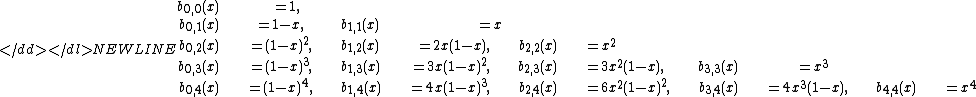
Properties
The Bernstein basis polynomials have the following properties:-
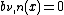 , if
, if 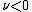 or
or 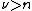 .
. -
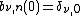 and
and 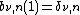 where
where 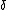 is the Kronecker delta function.
is the Kronecker delta function. -
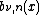 has a root with multiplicity
has a root with multiplicity  at point
at point 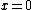 (note: if
(note: if 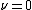 , there is no root at 0).
, there is no root at 0). -
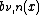 has a root with multiplicity
has a root with multiplicity 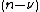 at point
at point 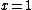 (note: if
(note: if  , there is no root at 1).
, there is no root at 1). -
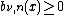 for
for 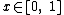 .
. -
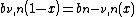 .
.
- The derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
can be written as a combination of two polynomials of lower degree: -
- The integralIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
is constant for a given
-
- If
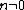 , then
, then 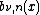 has a unique local maximum on the interval
has a unique local maximum on the interval 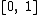 at
at 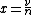 . This maximum takes the value:
. This maximum takes the value:
-
- The Bernstein basis polynomials of degree
 form a partition of unity:
form a partition of unity:
-
- By taking the first derivative of
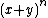 where
where 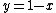 , it can be shown that
, it can be shown that
-
- The second derivative of
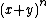 where
where 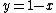 can be used to show
can be used to show
-
- A Bernstein polynomial can always be written as a linear combination of polynomials of higher degree:
-
Approximating continuous functions
Let ƒ be a continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on the interval [0, 1]. Consider the Bernstein polynomial
It can be shown that
uniformly on the interval [0, 1]. This is a stronger statement than the proposition that the limit holds for each value of x separately; that would be pointwise convergencePointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
rather than uniform convergence. Specifically, the word uniformly signifies that
Bernstein polynomials thus afford one way to prove the Weierstrass approximation theorem that every real-valued continuous function on a real interval [a, b] can be uniformly approximated by polynomial functions over R.
A more general statement for a function with continuous k-th derivative is
where additionally
is an eigenvalue of Bn; the corresponding eigenfunction is a polynomial of degree k.
Proof
Suppose K is a random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
distributed as the number of successes in n independent Bernoulli trialBernoulli trialIn the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
s with probability x of success on each trial; in other words, K has a binomial distribution with parameters n and x. Then we have the expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
E(K/n) = x.
By the weak law of large numbersLaw of large numbersIn probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
of probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
,
for every δ > 0. Moreover, this relation holds uniformly in x, which can be seen from its proof via Chebyshev's inequalityChebyshev's inequalityIn probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
, taking into account that the variance of K/n, equal to x(1-x)/n, is bounded from above by 1/(4n) irrespective of x.
Because ƒ, being continuous on a closed bounded interval, must be uniformly continuousUniform continuityIn mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
on that interval, one infers a statement of the form
uniformly in x. Taking into account that ƒ is bounded (on the given interval) one gets for the expectation
uniformly in x. To this end one splits the sum for the expectation in two parts. On one part the difference does not exceed ε; this part cannot contribute more than ε.
On the other part the difference exceeds ε, but does not exceed 2M, where M is an upper bound for |ƒ(x)|; this part cannot contribute more than 2M times the small probability that the difference exceeds ε.
Finally, one observes that the absolute value of the difference between expectations never exceeds the expectation of the absolute value of the difference, and that E(ƒ(K/n)) is just the Bernstein polynomial Bn(ƒ, x).
See for instance.
See also
- Bézier curveBézier curveA Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case....
- Polynomial interpolationPolynomial interpolationIn numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
- Newton formNewton polynomialIn the mathematical field of numerical analysis, a Newton polynomial, named after its inventor Isaac Newton, is the interpolation polynomial for a given set of data points in the Newton form...
- Lagrange formLagrange polynomialIn numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
-