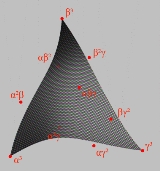
Bézier triangle
Encyclopedia
A Bézier triangle is a special type of Bézier surface
, which is created by (linear, quadratic, cubic or higher degree) interpolation of control points.
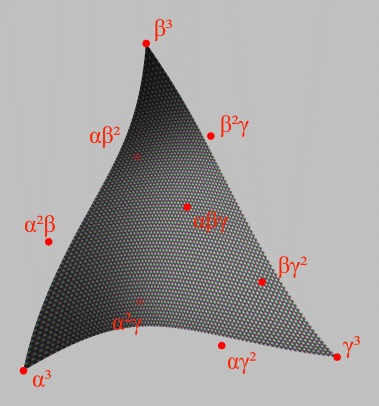A cubic Bézier triangle is a surface
with the equation
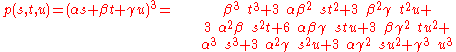
where α3, β3, γ3, α2β, αβ2, β2γ, βγ2, αγ2, α2γ and αβγ are the control points of the triangle and s, t, u (with 0 ≤ s, t, u ≤ 1 and s+t+u=1) the barycentric coordinates
inside the triangle.
The corners of the triangle are the points α3, β3 and γ3. The edges of the triangle are themselves Bézier curve
s, with the same control points as the Bézier triangle.
By removing the γu term, a regular Bézier curve results. Also, while not very useful for display on a physical computer screen, by adding extra terms, a Bézier tetrahedron
or Bézier polytope
results.
Due to the nature of the equation, the entire triangle will be contained within the volume surrounded by the control points, and affine transformation
s of the control points will correctly transform the whole triangle in the same way.
dividing the Bézier triangle into two separate Bézier triangles, until they are considered sufficiently small, using only addition and division by two, not requiring any floating point
arithmetic whatsoever.
The following computes the new control points for the half of the full Bézier triangle with the corner α3, a corner halfway along the Bézier curve between α3 and β3, and the third corner γ3.
or other degrees of Bézier triangles, by changing the exponent in the original equation, in which case there will be more or fewer control points. With the exponent 1 (one), the resulting Bézier triangle is actually a regular flat triangle
. In all cases, the edges of the triangle will be Bézier curves of the same degree.
A general nth-order Bézier triangle has (n + 1)(n + 2)/2 control points a i ß j γ k where i, j, k are nonnegative integers such that i + j + k = n. The surface is then defined as
Bézier surface
Bézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modeling.As with the Bézier curve, a Bézier surface is defined by a set of control points...
, which is created by (linear, quadratic, cubic or higher degree) interpolation of control points.
Cubic Bézier Triangle
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
with the equation
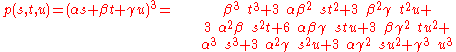
where α3, β3, γ3, α2β, αβ2, β2γ, βγ2, αγ2, α2γ and αβγ are the control points of the triangle and s, t, u (with 0 ≤ s, t, u ≤ 1 and s+t+u=1) the barycentric coordinates
Barycentric coordinates (mathematics)
In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...
inside the triangle.
The corners of the triangle are the points α3, β3 and γ3. The edges of the triangle are themselves Bézier curve
Bézier curve
A Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case....
s, with the same control points as the Bézier triangle.
By removing the γu term, a regular Bézier curve results. Also, while not very useful for display on a physical computer screen, by adding extra terms, a Bézier tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
or Bézier polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
results.
Due to the nature of the equation, the entire triangle will be contained within the volume surrounded by the control points, and affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s of the control points will correctly transform the whole triangle in the same way.
Halving a Cubic Bézier Triangle
An advantage of Bézier triangles in computer graphics is, they are smooth, and can easily be approximated by regular triangles, by recursivelyRecursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
dividing the Bézier triangle into two separate Bézier triangles, until they are considered sufficiently small, using only addition and division by two, not requiring any floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
arithmetic whatsoever.
The following computes the new control points for the half of the full Bézier triangle with the corner α3, a corner halfway along the Bézier curve between α3 and β3, and the third corner γ3.
- equivalently, using addition and division by two only,
-
β3 := (αβ2 + β3)/2 αβ2 := (α2β + αβ2)/2 β3 := (αβ2 + β3)/2 α2β := (α3 + α2β)/2 αβ2 := (α2β + αβ2)/2 β3 := (αβ2 + β3)/2 β2γ := (αβγ + β2γ)/2 αβγ := (α2γ + αβγ)/2 β2γ:=(αβγ+β2γ)/2 βγ2 := (αγ2 + βγ2)/2 - where := means to replace the vector on the left with the vector on the right.
- Note that halving a bézier triangle is similar to halving Bézier curves of all orders up to the order of the Bézier triangle.
nth-order Bézier Triangle
It is also possible to create quadraticQuadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
or other degrees of Bézier triangles, by changing the exponent in the original equation, in which case there will be more or fewer control points. With the exponent 1 (one), the resulting Bézier triangle is actually a regular flat triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
. In all cases, the edges of the triangle will be Bézier curves of the same degree.
A general nth-order Bézier triangle has (n + 1)(n + 2)/2 control points a i ß j γ k where i, j, k are nonnegative integers such that i + j + k = n. The surface is then defined as
-
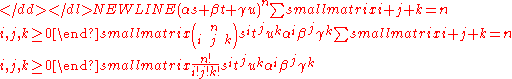
for all nonnegative real numbers s + t + u = 1.
See also
- Bézier curveBézier curveA Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case....
- Bézier surfaceBézier surfaceBézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modeling.As with the Bézier curve, a Bézier surface is defined by a set of control points...
(biquadratic patches are Bézier rectangles) - SurfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
External links
- Quadratic Bézier Triangles As Drawing Primitives Contains more info on planar and quadratic Bézier triangles.
- Paper about the use of cubic Bézier patches in raytracing (German)
- Ray Tracing Triangular Bézier Patches
- Triangular Bézier Clipping
- Curved PN triangles (a special kind of cubic Bézier triangles)
- Pixel-Shader-Based Curved Triangles
- Surface Construction with Near Least Square Acceleration based on Vertex Normals on Triangular Meshes
- Bézier curve