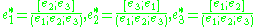Dual basis
Encyclopedia
In linear algebra, a dual basis is a set of vectors
that forms a basis
for the dual space
of a vector space. For a finite dimensional vector space V, the dual space V* is isomorphic to V, and for any given set of basis vectors {e1, …, en} of V, there is an associated dual basis {e1,...,en} of V* with the relation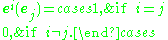
Concretely, we can write vectors in an n-dimensional vector space V as n×1 column matrices and elements of the dual space V* as 1×n row matrices that act as linear functionals by left matrix multiplication
.
For example, the standard basis vectors of R2 (the Cartesian plane) are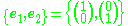
and the standard basis vectors of its dual space R2* are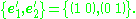
In 3-dimensional space, for a given basis {e1, e2, e3}, you can find the biorthogonal (dual) basis by these formulas:
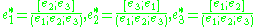
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
that forms a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of a vector space. For a finite dimensional vector space V, the dual space V* is isomorphic to V, and for any given set of basis vectors {e1, …, en} of V, there is an associated dual basis {e1,...,en} of V* with the relation
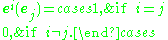
Concretely, we can write vectors in an n-dimensional vector space V as n×1 column matrices and elements of the dual space V* as 1×n row matrices that act as linear functionals by left matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
.
For example, the standard basis vectors of R2 (the Cartesian plane) are
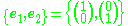
and the standard basis vectors of its dual space R2* are
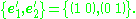
In 3-dimensional space, for a given basis {e1, e2, e3}, you can find the biorthogonal (dual) basis by these formulas: