Biorthogonal system
Encyclopedia
In mathematics
, a biorthogonal system is a pair of topological vector space
s E and F that are in duality
, with a pair of indexed subsets
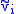in E and 
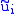in F
such that
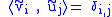
with the Kronecker delta. This applies, for example, with E = F = H a Hilbert space
; in which case a biorthogonal system reduces to an orthonormal system
. In L²[0,2π] the functions cos nx and sin nx form a biorthogonal system.
,
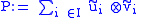where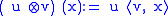
; its image is the linear span
of
, and the
kernel
is
.
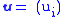and 
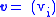the projection related is
,
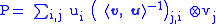where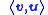
is the matrix with entries 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a biorthogonal system is a pair of topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s E and F that are in duality
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
, with a pair of indexed subsets
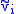in E and 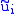in Fsuch that
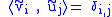
with the Kronecker delta. This applies, for example, with E = F = H a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
; in which case a biorthogonal system reduces to an orthonormal system
Orthogonal basis
In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...
. In L²[0,2π] the functions cos nx and sin nx form a biorthogonal system.
Projection
Related to a biorthogonal system is the projection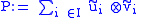,where
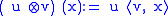; its image is the linear spanLinear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
of
, and thekernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
is
.Construction
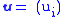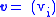Given a possibly non-orthogonal set of vectors and the projection related is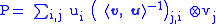,where
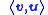is the matrix with entries .
-
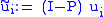, and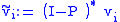 
then is an orthogonal system.