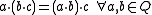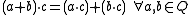Quasifield
Encyclopedia
In mathematics
, a quasifield is an algebraic structure
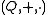where + and 
are binary operation
s on Q, much like a division ring
, but with some weaker conditions.
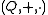is a structure, where + and . binary operations on Q, satisfying these axioms :
Strictly speaking, this is the definition of a left quasifield. A right quasifield is similarly defined, but satisfies right distributivity instead. A quasifield satisfying both distributive laws is called a semifield
, in the sense in which the term is used in projective geometry
.
Although not assumed, one can prove that the axioms imply that the additive group
is abelian
.
Restricting the binary operations + and
to K, one can shown that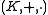 
is a division ring
.
One can now make a vector space of Q over K, with the following scalar multiplication :
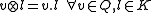
As the order of any finite division ring is a prime power
, this means that the order of any finite quasifield is also a prime power. Any division ring and any field is a quasi-field. The smallest quasifields are the finite fields of order
2,3,4,5,7, and 8. There are 5 different quasifields of order 9, only one of
which is a field; they are presented in (Hall 1959) and (Weibel 2007).
, we define a ternary map 
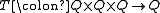by
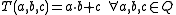
One can then verify that
satisfies the axioms of a planar ternary ring
. Associated to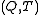
is its corresponding projective plane
. The projective planes constructed this way are characterized as follows;
the details of this relationship are given in (Hall 1959).
A projective plane is a translation plane
with respect to the line at infinity if and only if any (or all) of its associated planar ternary rings are right quasifields. (The plane does not uniquely determine the ring; all 4 nonabelian quasifields of order 9 are ternary rings for the unique non-Desarguesian translation plane of order 9.) It is called a "shear plane" if any (or all) of its ternary rings are left quasifield.
1907 paper (Veblen-Wedderburn 1907) by O. Veblen
and J. Wedderburn
. Surveys of quasifields and their applications to projective plane
s may be found in (Hall 1959) and (Weibel 2007).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quasifield is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
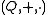where + and are binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s on Q, much like a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
, but with some weaker conditions.
Definition
A quasifield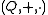 is a structure, where + and . binary operations on Q, satisfying these axioms :-
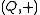is a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity... -
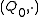is a loopQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
, where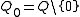
-
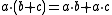
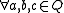(left distributivityDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
) -
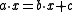has exactly one solution 
Strictly speaking, this is the definition of a left quasifield. A right quasifield is similarly defined, but satisfies right distributivity instead. A quasifield satisfying both distributive laws is called a semifield
Semifield
In mathematics, a semifield is an algebraic structure with two binary operations, addition and multiplication, which is similar to the field, but with some axioms relaxed...
, in the sense in which the term is used in projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
.
Although not assumed, one can prove that the axioms imply that the additive group
is abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
.
Kernel
The kernel K of a quasifield Q is the set of all elements c such that :
Restricting the binary operations + and
to K, one can shown that 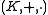is a division ringDivision ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
.
One can now make a vector space of Q over K, with the following scalar multiplication :
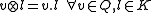
As the order of any finite division ring is a prime power
Prime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
, this means that the order of any finite quasifield is also a prime power. Any division ring and any field is a quasi-field. The smallest quasifields are the finite fields of order
2,3,4,5,7, and 8. There are 5 different quasifields of order 9, only one of
which is a field; they are presented in (Hall 1959) and (Weibel 2007).
Projective planes
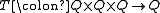Given a quasifield, we define a ternary map by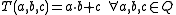One can then verify that
satisfies the axioms of a planar ternary ringPlanar ternary ring
In mathematics, a ternary ring is an algebraic structure consisting of a non-empty set R and a ternary mapping T \colon R^3 \to R, and a planar ternary ring or ternary field is special sort of a ternary ring used by to give coordinates to projective planes...
. Associated to
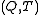is its corresponding projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
. The projective planes constructed this way are characterized as follows;
the details of this relationship are given in (Hall 1959).
A projective plane is a translation plane
Translation plane
In mathematics, a translation plane is a particular kind of projective plane, as considered as a combinatorial object.In a projective plane, \scriptstyle p represents a point, and \scriptstyle L represents a line. A central collineation with center \scriptstyle p and axis \scriptstyle L is a...
with respect to the line at infinity if and only if any (or all) of its associated planar ternary rings are right quasifields. (The plane does not uniquely determine the ring; all 4 nonabelian quasifields of order 9 are ternary rings for the unique non-Desarguesian translation plane of order 9.) It is called a "shear plane" if any (or all) of its ternary rings are left quasifield.
History
Quasifields were called "Veblen-Wedderburn systems" in the literature before 1975, since they were first studied in the1907 paper (Veblen-Wedderburn 1907) by O. Veblen
Oswald Veblen
Oswald Veblen was an American mathematician, geometer and topologist, whose work found application in atomic physics and the theory of relativity. He proved the Jordan curve theorem in 1905.-Life:...
and J. Wedderburn
Joseph Wedderburn
Joseph Henry Maclagan Wedderburn was a Scottish mathematician, who taught at Princeton University for most of his career. A significant algebraist, he proved that a finite division algebra is a field, and part of the Artin–Wedderburn theorem on simple algebras...
. Surveys of quasifields and their applications to projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
s may be found in (Hall 1959) and (Weibel 2007).