
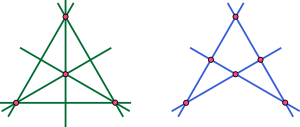
Arrangement of lines
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
an arrangement of lines is the partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the plane formed by a collection of lines
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
. Bounds on the complexity of arrangements have been studied in discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
, and computational geometers
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
have found algorithms for the efficient construction of arrangements.
Definition
For any set A of lines in the Euclidean plane, one can define an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the points of the plane according to which two points p and q are equivalent if, for every line l of A, either p and q are both on l or both belong to the same open half-plane bounded by l. When A is finite or locally finite the equivalence classes of this relation are of three types:
- the interiors of bounded or unbounded convex polygons (the cells of the arrangement), the connected componentConnected componentConnected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
s of the subset of the plane not contained in any of the lines of A, - open line segments and open infinite rays (the edges of the arrangement), the connected components of the points of a single line that do not belong to any other lines of A, and
- single points (the verticesVertex (geometry)In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of the arrangement), the intersections of two or more lines of A.
These three types of objects link together to form a cell complex covering the plane. Two arrangements are said to be isomorphic or combinatorially equivalent if there is a one-to-one adjacency-preserving correspondence between the objects in their associated cell complexes.
Complexity of arrangements
The study of arrangements was begun by Jakob SteinerJakob Steiner
Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
, who proved the first bounds on the maximum number of features of different types that an arrangement may have.
An arrangement with n lines has at most n(n − 1)/2
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
vertices, one per pair of crossing lines. This maximum is achieved for simple arrangements, those in which each two lines has a distinct pair of crossing points. In any arrangement there will be n infinite-downward rays, one per line; these rays separate n + 1 cells of the arrangement that are unbounded in the downward direction. The remaining cells all have a unique bottommost vertex, and each vertex is bottommost for a unique cell, so the number of cells in an arrangement is the number of vertices plus n + 1, or at most n(n + 1)/2 + 1; see lazy caterer's sequence
Lazy caterer's sequence
The lazy caterer's sequence, more formally known as the central polygonal numbers, describes the maximum number of pieces of a circle that can be made with a given number of straight cuts. For example, three cuts across a pancake will produce six pieces if the cuts all meet at a common point, but...
. The number of edges of the arrangement is at most n2, as may be seen either by using the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
to calculate it from the numbers of vertices and cells, or by observing that each line is partitioned into at most n edges by the other n − 1 lines; again, this worst-case bound is achieved for simple arrangements.
The zone of a line l in a line arrangement is the collection of cells having edges belonging to l. The zone theorem states that the total number of edges in the cells of a single zone is linear. More precisely, the total number of edges of the cells belonging to a single side of line l is at most 5n − 1, and the total number of edges of the cells belonging to both sides of l is at most
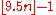 . More generally, the total complexity of the cells of a line arrangement that are intersected by any convex curve is O(n α(n)), where α denotes the inverse Ackermann function
. More generally, the total complexity of the cells of a line arrangement that are intersected by any convex curve is O(n α(n)), where α denotes the inverse Ackermann functionAckermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
, as may be shown using Davenport–Schinzel sequence
Davenport–Schinzel sequence
In combinatorics, a Davenport–Schinzel sequence is a sequence of symbols in which the number of times any two symbols may appear in alternation is limited. The maximum possible length of a Davenport–Schinzel sequence is bounded by the number of its distinct symbols multiplied by a small but...
s. Summing the complexities of all zones, one finds that the sum of squares of cell complexities in an arrangement is O(n2).
The k-level
K-set (geometry)
In discrete geometry, a k-set of a finite point set S in the Euclidean plane is a subset of k elements of S that can be strictly separated from the remaining points by a line. More generally, in Euclidean space of higher dimensions, a k-set of a finite point set is a subset of k elements that can...
of an arrangement is the polygonal chain formed by the edges that have exactly k other lines directly below them, and the ≤k-level is the portion of the arrangement below the k-level. Finding matching upper and lower bounds for the complexity of a k-level remains a major open problem in discrete geometry; the best upper bound is O(nk1/3), while the best lower bound is Ω(n exp(c (logk)1/2)). In contrast, the maximum complexity of the ≤k-level is known to be Θ(nk). A k-level is a special case of a monotone path in an arrangement; that is, a sequence of edges that intersects any vertical line in a single point. However, monotone paths may be much more complicated than k-levels: there exist arrangements and monotone paths in these arrangements where the number of points at which the path changes direction is Ω(n2 − o(1)).
Although a single cell in an arrangement may be bounded by all n lines, it is not possible in general for m different cells to all be bounded by n lines. Rather, the total complexity of m cells is at most Θ(m2/3n2/3 + n), almost the same bound as occurs in the Szemerédi–Trotter theorem
Szemerédi–Trotter theorem
The Szemerédi–Trotter theorem is a mathematical result in the field of combinatorial geometry. It asserts that given n points and m lines in the plane,the number of incidences The Szemerédi–Trotter theorem is a mathematical result in the field of combinatorial geometry. It asserts that given n...
on point-line incidences in the plane. A simple proof of this follows from the crossing number inequality
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
: if m cells have a total of x + n edges, one can form a graph with m nodes (one per cell) and x edges (one per pair of consecutive cells on the same line). The edges of this graph can be drawn as curves that do not cross within the cells corresponding to their endpoints, and then follow the lines of the arrangement; therefore, there are O(n2) crossings in this drawing. However, by the crossing number inequality, there are Ω(x3/m2) crossings; in order to satisfy both bounds, x must be O(m2/3n2/3).
Projective arrangements and projective duality
It is often convenient to study line arrangements not in the Euclidean plane but in the projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
, due to the fact that in projective geometry every pair of lines has a crossing point. In the projective plane, we may no longer define arrangements using sides of lines (a line in the projective plane does not separate the plane into two distinct sides), but we may still define the cells of an arrangement to be the connected components of the points not belonging to any line, the edges to be the connected components of sets of points belonging to a single line, and the vertices to be points where two or more lines cross. A line arrangement in the projective plane differs from its Euclidean counterpart in that the two Euclidean rays at either end of a line are replaced by a single edge in the projective plane that connects the leftmost and rightmost vertices on that line, and in that pairs of unbounded Euclidean cells are replaced in the projective plane by single cells that are crossed by the projective line at infinity.
Due to projective duality, many statements about the combinatorial properties of points in the plane may be more easily understood in an equivalent dual form about arrangements of lines. For instance, the Sylvester–Gallai theorem
Sylvester–Gallai theorem
The Sylvester–Gallai theorem asserts that given a finite number of points in the Euclidean plane, either# all the points are collinear; or# there is a line which contains exactly two of the points.This claim was posed as a problem by...
, stating that any non-collinear set of points in the plane has an ordinary line containing exactly two points, transforms under projective duality to the statement that any arrangement of lines with more than one vertex has an ordinary point, a vertex where only two lines cross. The earliest known proof of the Sylvester–Gallai theorem, by , uses the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
to show that such a vertex must always exist.
Triangles in arrangements
An arrangement of lines in the projective plane is said to be simplicial if every cell of the arrangement is bounded by exactly three edges; simplicial arrangements were first studied by Melchior. Three infinite families of simplicial line arrangements are known:- A near-pencil consisting of n − 1 lines through a single point, together with a single additional line that does not go through the same point,
- The family of lines formed by the sides of a regular polygonRegular polygonA regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
together with its axes of symmetry, and - The sides and axes of symmetry of an even regular polygon, together with the line at infinity.
Additionally there are many other examples of sporadic simplicial arrangements that do not fit into any known infinite family.
As Grünbaum writes, simplicial arrangements “appear as examples or counterexamples in many contexts of combinatorial geometry and its applications.” For instance, use simplicial arrangements to construct counterexamples to a conjecture on the relation between the degree of a set of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s and the number of invariant lines the equations may have. The two known counterexamples to the Dirac-Motzkin conjecture (which states that any n-line arrangement has at least n/2 ordinary points) are both simplicial.
The dual graph
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
of a line arrangement, in which there is one node per cell and one edge linking any pair of cells that share an edge of the arrangement, is a partial cube
Partial cube
In graph theory, a partial cube is a graph that is an isometric subgraph of a hypercube. In other words, a partial cube is a subgraph of a hypercube that preserves distances—the distance between any two vertices in the subgraph is the same as the distance between those vertices in the hypercube...
, a graph in which the nodes can be labeled by bitvectors in such a way that the graph distance equals the Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
between labels; in the case of a line arrangement, each coordinate of the labeling assigns 0 to nodes on one side of one of the lines and 1 to nodes on the other side. Dual graphs of simplicial arrangements have been used to construct infinite families of 3-regular
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
partial cubes, isomorphic to the graphs of simple zonohedra
Zonohedron
A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...
.
It is also of interest to study the extremal numbers of triangular cells in arrangements that may not necessarily be simplicial. In any arrangement, there must be at least n triangles; every arrangement that has only n triangles must be simple. The maximum possible number of triangles in a simple arrangement is known to be upper bounded by n(n − 1)/3 and lower bounded by n(n − 3)/3; the lower bound is achieved by certain subsets of the diagonals of a regular 2n-gon. For non-simple arrangements the maximum number of triangles is similar but more tightly bounded.
Multigrids and Penrose tilings

Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
, one per vertex of the arrangement, with sides perpendicular to the lines that meet at that vertex. These rhombi may be joined together to form a tiling of a convex polygon
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
in the case of an arrangement of finitely many lines, or of the entire plane in the case of a locally finite arrangement with infinitely many lines. investigated special cases of this construction in which the line arrangement consists of k sets of equally spaced parallel lines. For two perpendicular families of parallel lines this construction just gives the familiar square tiling of the plane, and for three families of lines at 120-degree angles from each other (themselves forming a trihexagonal tiling
Trihexagonal tiling
In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex...
) this produces the rhombille tiling. However, for more families of lines this construction produces aperiodic tiling
Aperiodic tiling
An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
s. In particular, for five families of lines at equal angles to each other (or, as de Bruijn calls this arrangement, a pentagrid) it produces a family of tilings that include the rhombic version of the Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
s.
The tetrakis square tiling
Tetrakis square tiling
In geometry, the tetrakis square tiling is a tiling of the Euclidean plane. It is square tiling with each square divided into four triangles from the center point, forming an infinite arrangement of lines....
is an infinite arrangement of lines forming a periodic tiling that resembles a multigrid with four parallel families, but in which two of the families are more widely spaced than the other two, and in which the arrangement is simplicial rather than simple. Its dual is the truncated square tiling
Truncated square tiling
In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon...
. Similarly, the triangular tiling is an infinite simplicial line arrangement with three parallel families, which has as its dual the hexagonal tiling, and the bisected hexagonal tiling is an infinite simplicial line arrangement with six parallel families and two line spacings, dual to the great rhombitrihexagonal tiling
Great rhombitrihexagonal tiling
In geometry, the truncated trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one square, one hexagon, and one dodecagon on each vertex...
.
Algorithms
Constructing an arrangement means, given as input a list of the lines in the arrangement, computing a representation of the vertices, edges, and cells of the arrangement together with the adjacencies between these objects, for instance as a doubly connected edge list. Due to the zone theorem, arrangements can be constructed efficiently by an incremental algorithm that adds one line at a time to the arrangement of the previously added lines: each new line can be added in time proportional to its zone, resulting in a total construction time of O(n2). However, the memory requirements of this algorithm are high, so it may be more convenient to report all features of an arrangement by an algorithm that does not keep the entire arrangement in memory at once. This may again be done efficiently, in time O(n2) and space O(n), by an algorithmic technique known as topological sweeping. Computing a line arrangement exactly requires a numerical precision several times greater than that of the input coordinates: if a line is specified by two points on it, the coordinates of the arrangement vertices may need four times as much precision as these input points. Therefore, computational geometers have also studied algorithms for constructing arrangements efficiently with limited numerical precision.As well, researchers have studied efficient algorithms for constructing smaller portions of an arrangement, such as zones, k-levels, or the set of cells containing a given set of points. The problem of finding the arrangement vertex with the median x-coordinate arises (in a dual form) in robust statistics
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
as the problem of computing the Theil–Sen estimator
Theil–Sen estimator
In non-parametric statistics, the Theil–Sen estimator, also known as Sen's slope estimator, slope selection, the single median method, or the Kendall robust line-fit method, is a method for robust linear regression that chooses the median slope among all lines through pairs of two-dimensional...
of a set of points.
Marc van Kreveld suggested the algorithmic problem of computing shortest paths between vertices in a line arrangement, where the paths are restricted to follow the edges of the arrangement, more quickly than the quadratic time that it would take to apply a shortest path algorithm to the whole arrangement graph. An approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
is known, and the problem may be solved efficiently for lines that fall into a small number of parallel families (as is typical for urban street grids), but the general problem remains open.
Other types of arrangement

Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s that share similar topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
properties with a line arrangement. These can be defined most simply in the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
as simple closed curves any two of which meet in a single crossing point. A pseudoline arrangement is said to be stretchable if it is combinatorially equivalent to a line arrangement; it is complete
Complete (complexity)
In computational complexity theory, a computational problem is complete for a complexity class if it is, in a formal sense, one of the "hardest" or "most expressive" problems in the complexity class...
for the existential theory of the reals
Existential theory of the reals
In mathematical logic, computational complexity theory, and computer science, the existential theory of the reals is the set of all true sentences of the form...
to distinguish stretchable arrangements from non-stretchable ones.
Arrangements of lines in the hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
have also been studied. Any finite set of lines in the Euclidean plane has a combinatorially equivalent arrangement in the hyperbolic plane (e.g. by enclosing the vertices of the arrangement by a large circle and interpreting the interior of the circle as a Klein model
Klein model
In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of n-dimensional hyperbolic geometry in which points are represented by the points in the interior of the n-dimensional unit ball and lines are represented by the...
of the hyperbolic plane). However, in hyperbolic line arrangements lines may avoid crossing each other without being parallel; the intersection graph
Intersection graph
In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
of the lines in a hyperbolic arrangement is a circle graph
Circle graph
In graph theory, a circle graph is the intersection graph of a set of chords of a circle. That is, it is an undirected graph whose vertices can be associated with chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.-Algorithmic...
. The corresponding concept to hyperbolic line arrangements for pseudolines is a weak pseudoline arrangement, a family of curves having the same topological properties as lines such that any two curves in the family either meet in a single crossing point or have no intersection.
More generally, geometers have studied arrangements of other types of curves in the plane, arrangements of hyperplanes
Arrangement of hyperplanes
In geometry and combinatorics, an arrangement of hyperplanes is a finite set A of hyperplanes in a linear, affine, or projective space S....
in higher dimensional spaces, and of other more complicated types of surface. Arrangements in complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s have also been studied; since complex lines do not partition the complex plane into multiple connected components, the combinatorics of vertices, edges, and cells does not apply to these types of space, but it is still of interest to study their symmetries and topological properties.
See also
- Configuration (geometry)Configuration (geometry)In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.Although certain specific...
, an arrangement of lines together with a subset of the vertices of the arrangement with the property that each vertex in the subset belongs to the same number of lines from the arrangement and each line from the arrangement contains the same number of vertices in the subset.

