Ample line bundle
Encyclopedia
In algebraic geometry
, a very ample line bundle
is one with enough global sections to set up an embedding
of its base variety
or manifold
into projective space
. An ample line bundle is one such that some positive power is very ample. Globally generated sheaves are those with enough sections to define a morphism to projective space.
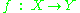, any vector bundle 
on Y, or more generally any sheaf in 
modules, eg. a coherent sheaf, can be pulled back to X, (see Inverse image functor
). This construction preserves the condition of being a line bundle, and more generally the rank.
The notions described in this article are related to this construction in the case of morphisms to projective spaces
and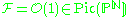 
,
the line bundle corresponding to the hyperplane divisor, whose sections are the 1-homogeneous regular functions. See Algebraic geometry of projective spaces#Divisors and twisting sheaves.
or a complex manifold and F a sheaf on X. One says that F is generated by (finitely many) global sections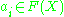
, if every stalk of F is generated as a module
over the stalk of the structure sheaf by the germs of the ai. For example, if F happens to be a line bundle, i.e. locally free of rank 1, this amounts to having finitely many global sections, such that for any point x in X, there is at least one section not vanishing at this point. In this case a choice of such global generators a0, ..., an gives a morphism
such that the pullback f*(O(1)) is F (Note that this evaluation makes sense when F is a subsheaf of the constant sheaf of rational functions on X). The converse statement is also true: given such a morphism f, the pullback of O(1) is generated by its global sections (on X).
X over a base scheme S or a complex manifold, a line bundle (or in other words an invertible sheaf
, that is, a locally free sheaf of rank one) L on X is said to be very ample, if there is an immersion i : X → PnS, the n-dimensional projective space over S for some n, such that the pullback
of the standard twisting sheaf O(1) on PnS is isomorphic to L:
Hence this notion is a special case of the previous one, namely a line bundle is very ample if it is globally generated and the morphism given by some global generators is an immersion.
Given a very ample sheaf L on X and a coherent sheaf
F, a theorem of Serre shows that (the coherent sheaf) F ⊗ L⊗n is generated by finitely many global sections for sufficiently large n. This in turn implies that global sections and higher (Zariski) cohomology
groups
are finitely generated. This is a distinctive feature of the projective situation. For example, for the affine n-space Ank over a field k, global sections of the structure sheaf O are polynomials in n variables, thus not a finitely generated k-vector space, whereas for Pnk, global sections are just constant functions, a one-dimensional k-vector space.
An equivalent, maybe more intuitive, definition of the ampleness of the line bundle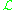
is its having a positive tensorial power that is very ample. In other words, for 
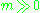there exists projective embeddings 
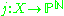such that 
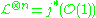, that is the zero divisors of global sections of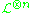 
are hyperplane sections.
This definition makes sense for the underlying divisors (Cartier divisors)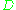
; an ample 
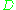is one where 
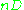moves in a large enough linear system
. Such divisors form a cone
in all divisors of those that are, in some sense, positive enough. The relationship with projective space is that the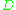
for a very ample 
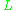corresponds to the hyperplane section
s (intersection with some hyperplane
) of the embedded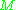
.
The equivalence between the two definitions is credited to Jean-Pierre Serre
in Faisceaux algébriques cohérents.
For curves, a divisor D is very ample if and only if
l(D) = 2 + l(D − A − B) whenever A and B are points. By the Riemann–Roch theorem
every divisor of degree
at least 2g&nsbp;+ 1 satisfies this condition so is very ample. This implies that a divisor is ample if and only if it has positive degree. The canonical divisor of degree 2g − 2 is very ample if and only if the curve is not
a hyperelliptic curve.
The Nakai–Moishezon criterion states that a Cartier divisor D on a proper scheme X over an algebraically closed field is ample if and only if Ddim(Y).Y > 0 for every closed integral subscheme Y of X. In the special case of curves this says that a divisor is ample if and only if it has positive degree, and for a smooth projective algebraic surface
S, the Nakai–Moishezon criterion states that D is ample if and only if its self-intersection number D.D is strictly positive, and for any irreducible curve C on S we have D.C > 0.
The Kleiman condition states that for any complete algebraic scheme X, a divisor D on X is ample if and only if D.C > 0 for any nonzero element C in the closure
of NE(X), the cone of curves
of X. In other words a divisor is ample if and only if it is in the interior of the real cone generated by nef divisors.
constructed divisors on surfaces that have positive intersection with every curve, but are not ample.
This shows that the condition D.D > 0 cannot be omitted in the Nakai–Moishezon criterion, and it is necessary to use the closure of NE(X) rather than NE(X) in the Kleiman condition.
showed that a line bundle L on a complete algebraic scheme is ample if and only if there is some positive ε such that
deg(L|C) ≥ εm(C) for all integral curves C in X, where m(C) is the
maximum of the multiplicities at the points of C.
-Serre
-Grothendieck states that for a line bundle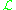
on a variety 
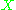, the following conditions are equivalent:
)
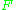on a variety is called ample if the invertible sheaf 
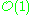on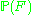 
is ample .
Ample vector bundles inherit many of the properties of ample line bundles.
, is that of a big line bundle. A line bundle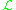
on X is said to be big if the equivalent following conditions are satisfied:
The interest of this notion is its stability with respect to rational transformations.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a very ample line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
is one with enough global sections to set up an embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of its base variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
or manifold
into projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. An ample line bundle is one such that some positive power is very ample. Globally generated sheaves are those with enough sections to define a morphism to projective space.
Inverse image of line bundle and hyperplane divisors
Given a morphism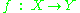, any vector bundle 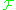on Y, or more generally any sheaf in 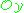modules, eg. a coherent sheaf, can be pulled back to X, (see Inverse image functorInverse image functor
In mathematics, the inverse image functor is a contravariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.-Definition:...
). This construction preserves the condition of being a line bundle, and more generally the rank.
The notions described in this article are related to this construction in the case of morphisms to projective spaces
and 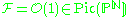,the line bundle corresponding to the hyperplane divisor, whose sections are the 1-homogeneous regular functions. See Algebraic geometry of projective spaces#Divisors and twisting sheaves.
Sheaves generated by their global sections
Let X be a schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
or a complex manifold and F a sheaf on X. One says that F is generated by (finitely many) global sections
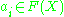, if every stalk of F is generated as a moduleModule
Module or modular may refer to the concept of modularity. It may also refer to:-Computing and engineering:* Modular design, the engineering discipline of designing complex devices using separately designed sub-components...
over the stalk of the structure sheaf by the germs of the ai. For example, if F happens to be a line bundle, i.e. locally free of rank 1, this amounts to having finitely many global sections, such that for any point x in X, there is at least one section not vanishing at this point. In this case a choice of such global generators a0, ..., an gives a morphism
- f: X → Pn, x ↦ [a0(x): ... : an(x)],
such that the pullback f*(O(1)) is F (Note that this evaluation makes sense when F is a subsheaf of the constant sheaf of rational functions on X). The converse statement is also true: given such a morphism f, the pullback of O(1) is generated by its global sections (on X).
Very ample line bundles
Given a schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
X over a base scheme S or a complex manifold, a line bundle (or in other words an invertible sheaf
Invertible sheaf
In mathematics, an invertible sheaf is a coherent sheaf S on a ringed space X, for which there is an inverse T with respect to tensor product of OX-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle...
, that is, a locally free sheaf of rank one) L on X is said to be very ample, if there is an immersion i : X → PnS, the n-dimensional projective space over S for some n, such that the pullback
Inverse image functor
In mathematics, the inverse image functor is a contravariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.-Definition:...
of the standard twisting sheaf O(1) on PnS is isomorphic to L:
- i*(O(1)) ≅ L.
Hence this notion is a special case of the previous one, namely a line bundle is very ample if it is globally generated and the morphism given by some global generators is an immersion.
Given a very ample sheaf L on X and a coherent sheaf
Coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
F, a theorem of Serre shows that (the coherent sheaf) F ⊗ L⊗n is generated by finitely many global sections for sufficiently large n. This in turn implies that global sections and higher (Zariski) cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
groups
- Hi(X, F)
are finitely generated. This is a distinctive feature of the projective situation. For example, for the affine n-space Ank over a field k, global sections of the structure sheaf O are polynomials in n variables, thus not a finitely generated k-vector space, whereas for Pnk, global sections are just constant functions, a one-dimensional k-vector space.
Definitions
The notion of ample line bundles L is slightly weaker than very ample line bundles: L is called ample if some tensor power L⊗n is very ample. This is equivalent to the following definition: L is ample if for any coherent sheaf F on X, there exists an integer n(F), such that F ⊗ L⊗n is generated by its global sections.An equivalent, maybe more intuitive, definition of the ampleness of the line bundle
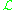is its having a positive tensorial power that is very ample. In other words, for 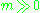there exists projective embeddings 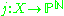such that 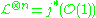, that is the zero divisors of global sections of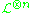 are hyperplane sections.
This definition makes sense for the underlying divisors (Cartier divisors)
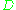; an ample 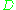is one where 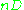moves in a large enough linear systemLinear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
. Such divisors form a cone
Cone (topology)
In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
in all divisors of those that are, in some sense, positive enough. The relationship with projective space is that the
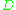for a very ample 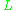corresponds to the hyperplane sectionHyperplane section
In mathematics, a hyperplane section of a subset X of projective space Pn is the intersection of X with some hyperplane H — in other words we look at the subset XH of those elements x of X that satisfy the single linear condition L = 0 defining H as a linear subspace...
s (intersection with some hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
) of the embedded
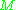.The equivalence between the two definitions is credited to Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
in Faisceaux algébriques cohérents.
Intersection theory
To decide in practice when a Cartier divisor D corresponds to an ample line bundle, there are some geometric criteria.For curves, a divisor D is very ample if and only if
l(D) = 2 + l(D − A − B) whenever A and B are points. By the Riemann–Roch theorem
Riemann–Roch theorem
The Riemann–Roch theorem is an important tool in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles...
every divisor of degree
at least 2g&nsbp;+ 1 satisfies this condition so is very ample. This implies that a divisor is ample if and only if it has positive degree. The canonical divisor of degree 2g − 2 is very ample if and only if the curve is not
a hyperelliptic curve.
The Nakai–Moishezon criterion states that a Cartier divisor D on a proper scheme X over an algebraically closed field is ample if and only if Ddim(Y).Y > 0 for every closed integral subscheme Y of X. In the special case of curves this says that a divisor is ample if and only if it has positive degree, and for a smooth projective algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
S, the Nakai–Moishezon criterion states that D is ample if and only if its self-intersection number D.D is strictly positive, and for any irreducible curve C on S we have D.C > 0.
The Kleiman condition states that for any complete algebraic scheme X, a divisor D on X is ample if and only if D.C > 0 for any nonzero element C in the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of NE(X), the cone of curves
Cone of curves
In mathematics, the cone of curves of an algebraic variety X is a combinatorial invariant of much importance to the birational geometry of X.-Definition:Let X be a proper variety...
of X. In other words a divisor is ample if and only if it is in the interior of the real cone generated by nef divisors.
constructed divisors on surfaces that have positive intersection with every curve, but are not ample.
This shows that the condition D.D > 0 cannot be omitted in the Nakai–Moishezon criterion, and it is necessary to use the closure of NE(X) rather than NE(X) in the Kleiman condition.
showed that a line bundle L on a complete algebraic scheme is ample if and only if there is some positive ε such that
deg(L|C) ≥ εm(C) for all integral curves C in X, where m(C) is the
maximum of the multiplicities at the points of C.
Sheaves cohomology
The theorem of CartanHenri Cartan
Henri Paul Cartan was a French mathematician with substantial contributions in algebraic topology. He was the son of the French mathematician Élie Cartan.-Life:...
-Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
-Grothendieck states that for a line bundle
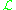on a variety 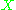, the following conditions are equivalent:
-
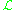is ample - for m big enough,
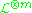is very ample - for any coherent sheaf
on X, the sheaf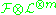 
is generated by global sections, for m big enough - for any coherent sheaf
on X, the higher cohomology groupsSheaf cohomologyIn mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
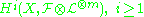vanish for m big enough.
Vector bundles of higher rank
A locally free sheaf (vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
)
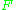on a variety is called ample if the invertible sheaf 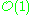on 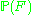is ample .Ample vector bundles inherit many of the properties of ample line bundles.
Big line bundles
An important generalization, notably in birational geometryBirational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
, is that of a big line bundle. A line bundle
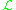on X is said to be big if the equivalent following conditions are satisfied:
is the tensor product of an ample line bundle and an effective line bundle- the Hilbert polynomialHilbert polynomialIn commutative algebra, the Hilbert polynomial of a graded commutative algebra or graded module is a polynomial in one variable that measures the rate of growth of the dimensions of its homogeneous components...
of the finitely generated graded ring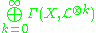
has degree the dimension of X - the rational mapping of the total system of divisorsLinear system of divisorsIn algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
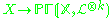is birational on its image for 
.
The interest of this notion is its stability with respect to rational transformations.
General algebraic geometry
- Cartier divisor
- Algebraic geometry of projective spacesAlgebraic geometry of projective spacesProjective spaces play a central role in algebraic geometry. The aim of this article is to define the notion in terms of abstract algebraic geometry and to describe some basic uses of those spaces.- Homogeneous polynomial ideals:...
- Fano varietyFano varietyIn algebraic geometry, a Fano variety, introduced by , is a non-singular complete variety whose anticanonical bundle is ample.Fano varieties are quite rare, compared to other families, like Calabi–Yau manifolds and general type surfaces....
: a variety whose Canonical line bundleCanonical line bundleThe canonical or tautological line bundle on a projective space appears frequently in mathematics, often in the study of characteristic classes...
is anti-ample
Ampleness in complex geometry
- Holomorphic vector bundleHolomorphic vector bundleIn mathematics, a holomorphic vector bundle is a complex vector bundle over a complex manifold X such that the total space E is a complex manifold and the projection map \pi:E\to X is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the...
- The Chern classChern classIn mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
is a characteristic form that detects ampleness of line bundles, this is the - Kodaira embedding theoremKodaira embedding theoremIn mathematics, the Kodaira embedding theorem characterises non-singular projective varieties, over the complex numbers, amongst compact Kähler manifolds...
: for compact complex manifolds, ampleness and positivity coincide. - Lefschetz hyperplane theoremLefschetz hyperplane theoremIn mathematics, specifically in algebraic geometry and algebraic topology, the Lefschetz hyperplane theorem is a precise statement of certain relations between the shape of an algebraic variety and the shape of its subvarieties...
: the study of very ample line bundles on complex projective manifolds gives strong topological information
Study references
- The slides on ampleness in Vladimir Lazić's Lectures on algebraic geometry