
Fano variety
Encyclopedia
In algebraic geometry
, a Fano variety, introduced by , is a non-singular complete variety
whose anticanonical bundle is ample
.
Fano varieties are quite rare, compared to other families, like Calabi–Yau manifolds and general type surfaces.
: the anticanonical line bundle
of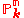 is
is 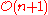 , which is very ample (its curvature
, which is very ample (its curvature
is n+1 times the Fubini–Study symplectic form).
Let D be a smooth Weil divisor in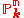 , from the adjunction formula, we infer
, from the adjunction formula, we infer 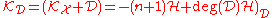 , where H is the class of the hyperplane. The hypersurface
, where H is the class of the hyperplane. The hypersurface
D is therefore Fano if and only if .
.
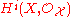 of the structure sheaf vanish for
of the structure sheaf vanish for  . In particular, the first Chern class induces an isomorphism
. In particular, the first Chern class induces an isomorphism 
A Fano variety is simply connected and is uniruled, in particular it has Kodaira dimension
−∞.
to the projective line
.
In dimension 2 they are del Pezzo surface
s and are isomorphic to either or to the projective plane blown up in at most 8 general points, and in particular are again all rational.
or to the projective plane blown up in at most 8 general points, and in particular are again all rational.
In dimension 3 there are non-rational examples. Iskovskih classified the Fano 3-folds with second Betti number
1 into 17 classes, and classified the ones with second Betti number at least 2, finding 88 deformation classes.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a Fano variety, introduced by , is a non-singular complete variety
Complete algebraic variety
In mathematics, in particular in algebraic geometry, a complete algebraic variety is an algebraic variety X, such that for any variety Y the projection morphismis a closed map, i.e. maps closed sets onto closed sets....
whose anticanonical bundle is ample
Ample line bundle
In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...
.
Fano varieties are quite rare, compared to other families, like Calabi–Yau manifolds and general type surfaces.
The example of projective hypersurfaces
The fundamental example of Fano varieties are the projective spacesAlgebraic geometry of projective spaces
Projective spaces play a central role in algebraic geometry. The aim of this article is to define the notion in terms of abstract algebraic geometry and to describe some basic uses of those spaces.- Homogeneous polynomial ideals:...
: the anticanonical line bundle
Canonical line bundle
The canonical or tautological line bundle on a projective space appears frequently in mathematics, often in the study of characteristic classes...
of
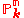 is
is 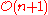 , which is very ample (its curvature
, which is very ample (its curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
is n+1 times the Fubini–Study symplectic form).
Let D be a smooth Weil divisor in
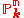 , from the adjunction formula, we infer
, from the adjunction formula, we infer 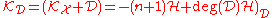 , where H is the class of the hyperplane. The hypersurface
, where H is the class of the hyperplane. The hypersurfaceHypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
D is therefore Fano if and only if
 .
.Some properties
The existence of an ample line bundle on Xis equivalent to X being a projective variety, so this is the case for Fano varieties. The Kodaira vanishing theorem implies that the higher cohomology groupsSheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
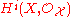 of the structure sheaf vanish for
of the structure sheaf vanish for  . In particular, the first Chern class induces an isomorphism
. In particular, the first Chern class induces an isomorphism 
A Fano variety is simply connected and is uniruled, in particular it has Kodaira dimension
Kodaira dimension
In algebraic geometry, the Kodaira dimension κ measures the size of the canonical model of a projective variety V.The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar.-The plurigenera:...
−∞.
Classification in small dimensions
Fano varieties in dimensions 1 are isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
.
In dimension 2 they are del Pezzo surface
Del Pezzo surface
In mathematics, a del Pezzo surface or Fano surface is a two-dimensional Fano variety, in other words a non-singular projective algebraic surface with ample anticanonical divisor class...
s and are isomorphic to either
 or to the projective plane blown up in at most 8 general points, and in particular are again all rational.
or to the projective plane blown up in at most 8 general points, and in particular are again all rational.In dimension 3 there are non-rational examples. Iskovskih classified the Fano 3-folds with second Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
1 into 17 classes, and classified the ones with second Betti number at least 2, finding 88 deformation classes.

