Holomorphic vector bundle
Encyclopedia
In mathematics
, a holomorphic vector bundle is a complex vector bundle over a complex manifold
X such that the total space E is a complex manifold and the projection map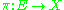
is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the holomorphic cotangent bundle. A holomorphic line bundle is a rank one holomorphic vector bundle.
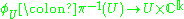
are biholomorphic maps. This is equivalent to requiring that the transition functions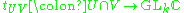
are holomorphic maps. The holomorphic structure on the tangent bundle of a complex manifold is guaranteed by the remark that the derivative (in the appropriate sense) of a vector-valued holomorphic function is itself holomorphic.
is said to be holomorphic if everywhere on U, it is holomorphic in some (equivalently any) trivialization.
This condition is local, so that holomorphic sections form a sheaf
on X, sometimes denoted
. If E is the trivial line bundle 
, then this sheaf coincides with the structure sheaf 
of the complex manifold X.
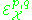denotes the sheaf of 
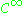differential forms of type (p,q), then the sheaf 
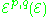of type (p,q) forms with values in E can be defined as the tensor product
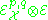. These sheaves are fine, which means that it has partitions of the unity.
A fundamental distinction between smooth and holomorphic vector bundles is that in the latter, there is a canonical differential operator : the Dolbeault operator
obtained in trivializations.
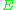is a holomorphic vector bundle of rank 
over 
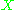, one denotes 
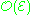the sheaf
of holomorphic sections of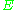
. Recall that it is a locally free sheaf of rank 
over the structure sheaf 
of its base.
The cohomology of the vector bundle is then defined as the sheaf cohomology
of
.
We have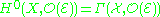
, the space of global holomorphic sections of E, whereas 
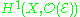parametrizes the group of extensions of the trivial line bundle of X by E, that is exact sequences of holomorphic vector bundles 
. For the group structure, see also Baer sum.
It can be equivalently defined as the first cohomology group
of the bundle of non-locally zero holomorphic functions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a holomorphic vector bundle is a complex vector bundle over a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
X such that the total space E is a complex manifold and the projection map
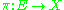is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the holomorphic cotangent bundle. A holomorphic line bundle is a rank one holomorphic vector bundle.Definition through trivialization
Specifically, one requires that the trivialization maps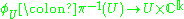are biholomorphic maps. This is equivalent to requiring that the transition functions
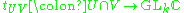
are holomorphic maps. The holomorphic structure on the tangent bundle of a complex manifold is guaranteed by the remark that the derivative (in the appropriate sense) of a vector-valued holomorphic function is itself holomorphic.
The sheaf of holomorphic sections
Let E be a holomorphic vector bundle. A local section is said to be holomorphic if everywhere on U, it is holomorphic in some (equivalently any) trivialization.This condition is local, so that holomorphic sections form a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on X, sometimes denoted
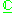. If E is the trivial line bundle , then this sheaf coincides with the structure sheaf of the complex manifold X.The sheaves of forms with values in a holomorphic vector bundles
If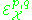 denotes the sheaf of 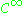differential forms of type (p,q), then the sheaf 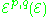of type (p,q) forms with values in E can be defined as the tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
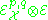. These sheaves are fine, which means that it has partitions of the unity.A fundamental distinction between smooth and holomorphic vector bundles is that in the latter, there is a canonical differential operator : the Dolbeault operator
obtained in trivializations.Cohomology of holomorphic vector bundles
If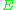 is a holomorphic vector bundle of rank over 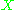, one denotes 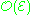the sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of holomorphic sections of
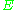. Recall that it is a locally free sheaf of rank over the structure sheaf of its base.The cohomology of the vector bundle is then defined as the sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
of
.We have
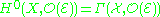, the space of global holomorphic sections of E, whereas 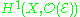parametrizes the group of extensions of the trivial line bundle of X by E, that is exact sequences of holomorphic vector bundles . For the group structure, see also Baer sum.The Picard group
In the context of complex differential geometry, the Picard group Pic(X) of the complex manifold X is the group of isomorphism classes of holomorphic line bundles with law the tensor product and inversion given by dualization.It can be equivalently defined as the first cohomology group
of the bundle of non-locally zero holomorphic functions.