Lefschetz hyperplane theorem
Encyclopedia
In mathematics
, specifically in algebraic geometry
and algebraic topology
, the Lefschetz hyperplane theorem is a precise statement of certain relations between the shape of an algebraic variety
and the shape of its subvarieties. More precisely, the theorem says that for a variety X embedded in projective space
and a hyperplane section
Y, the homology
, cohomology
, and homotopy group
s of X determine those of Y. A result of this kind was first stated by Solomon Lefschetz
for homology groups of complex algebraic varieties. Similar results have since been found for homotopy groups, in positive characteristic, and in other homology and cohomology theories.
Using a long exact sequence, one can show that each of these statements is equivalent to a vanishing theorem for certain relative topological invariants. In order, these are:
to prove the theorem. Rather than considering the hyperplane section Y alone, he put it into a family of hyperplane sections Yt, where Y = Y0. Because a generic hyperplane section is smooth, all but a finite number of Yt are smooth varieties. After removing these points from the t-plane and making an additional finite number of slits, the resulting family of hyperplane sections is topological trivial. That is, it is a product of a generic Yt with an open subset of the t-plane. X, therefore, can be understood if one understands how hyperplane sections are identified across the slits and at the singular points. Away from the singular points, the identification can be described inductively. At the singular points, the Morse lemma implies that there is a choice of coordinate system for X of a particularly simple form. This coordinate system can be used to prove the theorem directly.
. Here the parameter t plays the role of a Morse function. The basic tool in this approach is the Andreotti–Frankel theorem
, which states that a complex affine variety of complex dimension n (and thus real dimension 2n) has the homotopy type of a CW-complex of (real) dimension n. This implies that the relative homology
groups of Y in X are trivial in degree less than n. The long exact sequence of relative homology then gives the theorem.
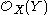is ample. Then the restriction map Hp,q(X) → Hp,q(Y) is an isomorphism if and is injective if p + q = n − 1. By Hodge theory, these cohomology groups are equal to the sheaf cohomology groups 
and 
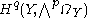. Therefore the theorem follows from applying the Akizuki–Nakano vanishing theorem to 
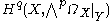and using a long exact sequence.
Combining this proof with the universal coefficient theorem
nearly yields the usual Lefschetz theorem for cohomology with coefficients in any field of characteristic zero. It is, however, slightly weaker because of the additional assumptions on Y.
and Alexander Grothendieck
found a generalization of the Lefschetz hyperplane theorem to the case where the coefficients of the cohomology lie not in a field but instead in a constructible sheaf
. They prove that for a constructible sheaf F on an affine variety U, the cohomology groups vanish whenever .
-adic cohomology. Up to some restrictions on the constructible sheaf, the Lefschetz theorem remains true for constructible sheaves in positive characteristic.
The theorem can also be generalized to intersection homology. In this setting, the theorem holds for highly singular spaces.
A Lefschetz-type theorem also holds for Picard groups.
Then in the cohomology ring
of X, the k-fold product with the cohomology class of a hyperplane gives an isomorphism between
and
This is the hard Lefschetz theorem, christened in French by Grothendieck more colloquially as the Théorème de Lefschetz vache. It immediately implies the injectivity part of the Lefschetz hyperplane theorem.
The hard Lefschetz theorem in fact holds for any compact Kaehler manifold, with the isomorphism in deRham cohomology given by multiplication by a power of the class of the Kaehler form. It can fail for non-Kaehler manifolds: for example, Hopf surface
s have vanishing second cohomology groups, so there is no analogue of the second cohomology class of a hyperplane section.
The hard Lefschetz theorem was proven for l-adic cohomology
of smooth projective varieties over finite fields by as a consequence of his work on the Weil conjectures
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the Lefschetz hyperplane theorem is a precise statement of certain relations between the shape of an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
and the shape of its subvarieties. More precisely, the theorem says that for a variety X embedded in projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
and a hyperplane section
Hyperplane section
In mathematics, a hyperplane section of a subset X of projective space Pn is the intersection of X with some hyperplane H — in other words we look at the subset XH of those elements x of X that satisfy the single linear condition L = 0 defining H as a linear subspace...
Y, the homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
, cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
, and homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of X determine those of Y. A result of this kind was first stated by Solomon Lefschetz
Solomon Lefschetz
Solomon Lefschetz was an American mathematician who did fundamental work on algebraic topology, its applications to algebraic geometry, and the theory of non-linear ordinary differential equations.-Life:...
for homology groups of complex algebraic varieties. Similar results have since been found for homotopy groups, in positive characteristic, and in other homology and cohomology theories.
The Lefschetz hyperplane theorem for complex projective varieties
Let X be an n-dimensional complex projective algebraic variety in CPN, and let Y be a hyperplane section of X such that U = X ∖ Y is smooth. The Lefschetz theorem refers to any of the following statements:- The natural map in Hk(Y, Z) → Hk(X, Z) in singular homology is an isomorphism for k < n − 1 and is surjective for k = n − 1.
- The natural map in Hk(X, Z) → Hk(Y, Z) in singular cohomology is an isomorphism for k < n − 1 and is injective for k = n − 1.
- The natural map πk(Y, Z) → πk(X, Z) is an isomorphism for k < n − 1 and is surjective for k = n − 1.
Using a long exact sequence, one can show that each of these statements is equivalent to a vanishing theorem for certain relative topological invariants. In order, these are:
- The relative singular homology groups Hk(X, Y, Z) are zero for
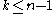. - The relative singular cohomology groups Hk(X, Y, Z) are zero for
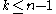. - The relative homotopy groups πk(X, Y) are zero for
.
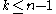Lefschetz's proof
Lefschetz used his idea of a Lefschetz pencilLefschetz pencil
In mathematics, a Lefschetz pencil is a construction in algebraic geometry considered by Solomon Lefschetz, in order to analyse the algebraic topology of an algebraic variety V. A pencil here is a particular kind of linear system of divisors on V, namely a one-parameter family, parametrised by the...
to prove the theorem. Rather than considering the hyperplane section Y alone, he put it into a family of hyperplane sections Yt, where Y = Y0. Because a generic hyperplane section is smooth, all but a finite number of Yt are smooth varieties. After removing these points from the t-plane and making an additional finite number of slits, the resulting family of hyperplane sections is topological trivial. That is, it is a product of a generic Yt with an open subset of the t-plane. X, therefore, can be understood if one understands how hyperplane sections are identified across the slits and at the singular points. Away from the singular points, the identification can be described inductively. At the singular points, the Morse lemma implies that there is a choice of coordinate system for X of a particularly simple form. This coordinate system can be used to prove the theorem directly.
Andreotti and Frankel's proof
Andreotti and Frankel recognized that Lefschetz's theorem could be recast using Morse theoryMorse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
. Here the parameter t plays the role of a Morse function. The basic tool in this approach is the Andreotti–Frankel theorem
Andreotti–Frankel theorem
In mathematics, the Andreotti–Frankel theorem from 1959 states that if V is a smooth affine variety of complex dimension n or, more generally, if V is any Stein manifold of dimension n, then in fact V is homotopy equivalent to a CW complex of real dimension at most n...
, which states that a complex affine variety of complex dimension n (and thus real dimension 2n) has the homotopy type of a CW-complex of (real) dimension n. This implies that the relative homology
Relative homology
In algebraic topology, a branch of mathematics, the homology of a topological space relative to a subspace is a construction in singular homology, for pairs of spaces. The relative homology is useful and important in several ways...
groups of Y in X are trivial in degree less than n. The long exact sequence of relative homology then gives the theorem.
Thom's and Bott's proofs
Neither Lefschetz's proof nor Andreotti and Frankel's proof directly imply the Lefschetz hyperplane theorem for homotopy groups. An approach that does was found by Thom no later than 1957 and was simplified and published by Bott in 1959. Thom and Bott interpret Y as the vanishing locus in X of a section of a line bundle. An application of Morse theory to this section implies that X can be constructed from Y by adjoining cells of dimension n or more. From this, it follows that the relative homology and homotopy groups of Y in X are concentrated in degrees n and higher, which yields the theorem.Kodaira and Spencer's proof for Hodge groups
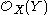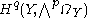Kodaira and Spencer found that under certain restrictions, it is possible to prove a Lefschetz-type theorem for the Hodge groups Hp,q. Specifically, assume that Y is smooth and that the line bundle is ample. Then the restriction map Hp,q(X) → Hp,q(Y) is an isomorphism if and is injective if p + q = n − 1. By Hodge theory, these cohomology groups are equal to the sheaf cohomology groups and . Therefore the theorem follows from applying the Akizuki–Nakano vanishing theorem to 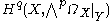and using a long exact sequence.Combining this proof with the universal coefficient theorem
Universal coefficient theorem
In mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A...
nearly yields the usual Lefschetz theorem for cohomology with coefficients in any field of characteristic zero. It is, however, slightly weaker because of the additional assumptions on Y.
Artin and Grothendieck's proof for constructible sheaves
Michael ArtinMichael Artin
Michael Artin is an American mathematician and a professor emeritus in the Massachusetts Institute of Technology mathematics department, known for his contributions to algebraic geometry. and also generally recognized as one of the outstanding professors in his field.Artin was born in Hamburg,...
and Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
found a generalization of the Lefschetz hyperplane theorem to the case where the coefficients of the cohomology lie not in a field but instead in a constructible sheaf
Constructible sheaf
In mathematics, a constructible sheaf is a sheaf of abelian groups over some topological space X, such that X is the union of a finite number of locally closed subsets on each of which the sheaf is a twisted constant sheaf...
. They prove that for a constructible sheaf F on an affine variety U, the cohomology groups vanish whenever .
The Lefschetz theorem in other cohomology theories
The motivation behind Artin and Grothendieck's proof for constructible sheaves was to give a proof that could be adapted to the setting of étale and-adic cohomology. Up to some restrictions on the constructible sheaf, the Lefschetz theorem remains true for constructible sheaves in positive characteristic.The theorem can also be generalized to intersection homology. In this setting, the theorem holds for highly singular spaces.
A Lefschetz-type theorem also holds for Picard groups.
Hard Lefschetz theorem
Let X be a n-dimensional non-singular complex projective variety in CPN.Then in the cohomology ring
Cohomology ring
In mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
of X, the k-fold product with the cohomology class of a hyperplane gives an isomorphism between
- Hn − k
and
- Hn + k.
This is the hard Lefschetz theorem, christened in French by Grothendieck more colloquially as the Théorème de Lefschetz vache. It immediately implies the injectivity part of the Lefschetz hyperplane theorem.
The hard Lefschetz theorem in fact holds for any compact Kaehler manifold, with the isomorphism in deRham cohomology given by multiplication by a power of the class of the Kaehler form. It can fail for non-Kaehler manifolds: for example, Hopf surface
Hopf surface
In complex geometry, a Hopf surface is a compact complex surface obtainedas a quotient of the complex vector space C2 \ 0...
s have vanishing second cohomology groups, so there is no analogue of the second cohomology class of a hyperplane section.
The hard Lefschetz theorem was proven for l-adic cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
of smooth projective varieties over finite fields by as a consequence of his work on the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
.