All-pass filter
Encyclopedia
An all-pass filter is a signal processing filter
that passes all frequencies
equally, but changes the phase
relationship between various frequencies. It does this by varying its propagation delay
with frequency. Generally, the filter is described by the frequency at which the phase shift crosses 90° (i.e., when the input and output signals go into quadrature
— when there is a quarter wavelength
of delay between them).
They are generally used to compensate for other undesired phase shifts that arise in the system, or for mixing with an unshifted version of the original to implement a notch comb filter
.
They may also be used to convert a mixed phase filter into a minimum phase
filter with an equivalent magnitude response or an unstable filter into a stable filter with an equivalent magnitude response.
circuit shown in Figure 1 implements an active
all-pass filter with the transfer function
which has one pole at -1/RC and one zero
at 1/RC (i.e., they are reflections of each other across the imaginary
axis of the complex plane
). The magnitude and phase
of H(iω) for some angular frequency
ω are
As expected, the filter has unity-gain
magnitude for all ω. The filter introduces a different delay at each frequency and reaches input-to-output quadrature
at ω=1/RC (i.e., phase shift is 90 degrees).
This implementation uses a high-pass filter
at the non-inverting input to generate the phase shift and negative feedback
to compensate for the filter's attenuation
.
In fact, the phase shift of the all-pass filter is double the phase shift of the high-pass filter at its non-inverting input.
into a low-pass filter
. The result is a phase shifter with the same quadrature frequency but a 180 degree shift at high frequencies and no shift at low frequencies. In other words, the transfer function is negated
, and so it has the same pole at -1/RC and reflected zero at 1/RC. Again, the phase shift of the all-pass filter is double the phase shift of the first-order filter at its non-inverting input.
in its ohmic mode to implement a voltage-controlled phase shifter; the voltage on the gate adjusts the phase shift. In electronic music, a phaser
typically consists of four or six of these phase-shifting sections connected in tandem and summed with the original. A low-frequency oscillator (LFO) ramps the control voltage to produce the characteristic swooshing sound.
can be canceled and reflected on the left-hand plane.
like operational amplifiers is that they do not require inductor
s, which are bulky and costly in integrated circuit
designs. In other applications where inductors are readily available,
all-pass filters can be implemented entirely without active components. There are a number of circuit topologies
that can be used for this. The following are the most commonly used circuits.
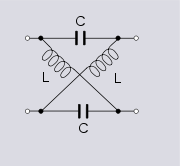
The lattice phase equaliser, or filter, is a filter composed of lattice, or X-sections. With single element branches it can produce a phase shift up to 180°, and with resonant branches it can produce phase shifts up to 360°. The filter is an example of a constant-resistance network (i.e., its image impedance
is constant over all frequencies).
like a low pass filter it is different in that the two inductor branches are mutually coupled. This results in transformer action between the two inductors and an all-pass response even at high frequency.
s being used for stereophonic sound
broadcasts. This application requires that the filter has a linear phase
response with frequency (i.e., constant group delay
) over a wide bandwidth and is the reason for choosing this topology.
implementation of an all-pass filter with a complex pole at
is
which has a zero at
, where 
denotes the complex conjugate
. The pole and zero sit at the same angle but have reciprocal magnitudes (i.e., they are reflections of each other across the boundary of the complex
unit circle
). The placement of this pole-zero pair for a given
can be rotated in the complex plane by any angle and retain its all-pass magnitude characteristic. Complex pole-zero pairs in all-pass filters help control the frequency where phase shifts occur.
To create an all-pass implementation with real coefficients, the complex all-pass filter can be cascaded with an all-pass that substitutes
for 
, leading to the Z-transform
implementation
which is equivalent to the difference equation
where
is the output and 
is the input at discrete time step 
.
Filters such as the above can be cascaded with unstable or mixed-phase filters to create a stable or minimum-phase filter without changing the magnitude response of the system. For example, by proper choice of
, a pole of an unstable system that is outside of the unit circle
can be canceled and reflected inside the unit circle.
Filter (signal processing)
In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...
that passes all frequencies
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
equally, but changes the phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
relationship between various frequencies. It does this by varying its propagation delay
Propagation delay
Propagation delay is a technical term that can have a different meaning depending on the context. It can relate to networking, electronics or physics...
with frequency. Generally, the filter is described by the frequency at which the phase shift crosses 90° (i.e., when the input and output signals go into quadrature
Quadrature
Quadrature may refer to:In signal processing:*Quadrature amplitude modulation , a modulation method of using both an carrier wave and a 'quadrature' carrier wave that is 90° out of phase with the main, or in-phase, carrier...
— when there is a quarter wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of delay between them).
They are generally used to compensate for other undesired phase shifts that arise in the system, or for mixing with an unshifted version of the original to implement a notch comb filter
Comb filter
In signal processing, a comb filter adds a delayed version of a signal to itself, causing constructive and destructive interference. The frequency response of a comb filter consists of a series of regularly spaced spikes, giving the appearance of a comb....
.
They may also be used to convert a mixed phase filter into a minimum phase
Minimum phase
In control theory and signal processing, a linear, time-invariant system is said to be minimum-phase if the system and its inverse are causal and stable....
filter with an equivalent magnitude response or an unstable filter into a stable filter with an equivalent magnitude response.
Active analog implementation
The operational amplifierOperational amplifier
An operational amplifier is a DC-coupled high-gain electronic voltage amplifier with a differential input and, usually, a single-ended output...
circuit shown in Figure 1 implements an active
Passivity (engineering)
Passivity is a property of engineering systems, used in a variety of engineering disciplines, but most commonly found in analog electronics and control systems...
all-pass filter with the transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
which has one pole at -1/RC and one zero
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
at 1/RC (i.e., they are reflections of each other across the imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
axis of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
). The magnitude and phase
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
of H(iω) for some angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
ω are
As expected, the filter has unity-gain
Gain
In electronics, gain is a measure of the ability of a circuit to increase the power or amplitude of a signal from the input to the output. It is usually defined as the mean ratio of the signal output of a system to the signal input of the same system. It may also be defined on a logarithmic scale,...
magnitude for all ω. The filter introduces a different delay at each frequency and reaches input-to-output quadrature
Quadrature
Quadrature may refer to:In signal processing:*Quadrature amplitude modulation , a modulation method of using both an carrier wave and a 'quadrature' carrier wave that is 90° out of phase with the main, or in-phase, carrier...
at ω=1/RC (i.e., phase shift is 90 degrees).
This implementation uses a high-pass filter
High-pass filter
A high-pass filter is a device that passes high frequencies and attenuates frequencies lower than its cutoff frequency. A high-pass filter is usually modeled as a linear time-invariant system...
at the non-inverting input to generate the phase shift and negative feedback
Negative feedback
Negative feedback occurs when the output of a system acts to oppose changes to the input of the system, with the result that the changes are attenuated. If the overall feedback of the system is negative, then the system will tend to be stable.- Overview :...
to compensate for the filter's attenuation
Attenuation
In physics, attenuation is the gradual loss in intensity of any kind of flux through a medium. For instance, sunlight is attenuated by dark glasses, X-rays are attenuated by lead, and light and sound are attenuated by water.In electrical engineering and telecommunications, attenuation affects the...
.
- At high frequenciesFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
, the capacitorCapacitorA capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
is a short circuitShort circuitA short circuit in an electrical circuit that allows a current to travel along an unintended path, often where essentially no electrical impedance is encountered....
, thereby creating a unity-gainGainIn electronics, gain is a measure of the ability of a circuit to increase the power or amplitude of a signal from the input to the output. It is usually defined as the mean ratio of the signal output of a system to the signal input of the same system. It may also be defined on a logarithmic scale,...
voltage buffer (i.e., no phase shift). - At low frequencies and DC, the capacitor is an open circuitOpen circuitThe term Open circuit may refer to:*Open-circuit scuba, a type of SCUBA-diving equipment where the user breathes from the set and then exhales to the surroundings without recycling the exhaled air...
and the circuit is an inverting amplifier (i.e., 180 degree phase shift) with unity gain. - At the corner frequency ω=1/RC of the high-pass filter (i.e., when input frequency is 1/(2πRC)), the circuit introduces a 90 degree shift (i.e., output is in quadrature with input; it is delayed by a quarter wavelengthWavelengthIn physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
).
In fact, the phase shift of the all-pass filter is double the phase shift of the high-pass filter at its non-inverting input.
Implementation using low-pass filter
A similar all-pass filter can be implemented by interchanging the position of the resistor and capacitor, which turns the high-pass filterHigh-pass filter
A high-pass filter is a device that passes high frequencies and attenuates frequencies lower than its cutoff frequency. A high-pass filter is usually modeled as a linear time-invariant system...
into a low-pass filter
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
. The result is a phase shifter with the same quadrature frequency but a 180 degree shift at high frequencies and no shift at low frequencies. In other words, the transfer function is negated
Negation (disambiguation)
Negation may refer to:* Negation , the operation in mathematics that takes x to −x, mapping positive numbers to negative numbers and the other way around, equivalent to reversing the sign of a number...
, and so it has the same pole at -1/RC and reflected zero at 1/RC. Again, the phase shift of the all-pass filter is double the phase shift of the first-order filter at its non-inverting input.
Voltage controlled implementation
The resistor can be replaced with a FETField-effect transistor
The field-effect transistor is a transistor that relies on an electric field to control the shape and hence the conductivity of a channel of one type of charge carrier in a semiconductor material. FETs are sometimes called unipolar transistors to contrast their single-carrier-type operation with...
in its ohmic mode to implement a voltage-controlled phase shifter; the voltage on the gate adjusts the phase shift. In electronic music, a phaser
Phaser (effect)
A phaser is an audio signal processing technique used to filter a signal by creating a series of peaks and troughs in the frequency spectrum. The position of the peaks and troughs is typically modulated so that they vary over time, creating a sweeping effect...
typically consists of four or six of these phase-shifting sections connected in tandem and summed with the original. A low-frequency oscillator (LFO) ramps the control voltage to produce the characteristic swooshing sound.
General usage
These circuits are used as phase shifters and in systems of phase shaping and time delay. Filters such as the above can be cascaded with unstable or mixed-phase filters to create a stable or minimum-phase filter without changing the magnitude response of the system. For example, by proper choice of pole (and therefore zero), a pole of an unstable system that is in the right-hand planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
can be canceled and reflected on the left-hand plane.
Passive analog implementation
The benefit to implementing all-pass filters with active componentsPassivity (engineering)
Passivity is a property of engineering systems, used in a variety of engineering disciplines, but most commonly found in analog electronics and control systems...
like operational amplifiers is that they do not require inductor
Inductor
An inductor is a passive two-terminal electrical component used to store energy in a magnetic field. An inductor's ability to store magnetic energy is measured by its inductance, in units of henries...
s, which are bulky and costly in integrated circuit
Integrated circuit
An integrated circuit or monolithic integrated circuit is an electronic circuit manufactured by the patterned diffusion of trace elements into the surface of a thin substrate of semiconductor material...
designs. In other applications where inductors are readily available,
all-pass filters can be implemented entirely without active components. There are a number of circuit topologies
Topology (electronics)
The topology of an electronic circuit is the form taken by the network of interconnections of the circuit components. Different specific values or ratings of the components are regarded as being the same topology....
that can be used for this. The following are the most commonly used circuits.
Lattice filter
The lattice phase equaliser, or filter, is a filter composed of lattice, or X-sections. With single element branches it can produce a phase shift up to 180°, and with resonant branches it can produce phase shifts up to 360°. The filter is an example of a constant-resistance network (i.e., its image impedance
Image impedance
Image impedance is a concept used in electronic network design and analysis and most especially in filter design. The term image impedance applies to the impedance seen looking in to the ports of a network. Usually a two-port network is implied but the concept is capable of being extended to...
is constant over all frequencies).
T-section filter
The phase equaliser based on T topology is the unbalanced equivalent of the lattice filter and has the same phase response. While the circuit diagram may looklike a low pass filter it is different in that the two inductor branches are mutually coupled. This results in transformer action between the two inductors and an all-pass response even at high frequency.
Bridged T-section filter
The bridged T topology is used for delay equalisation, particularly the differential delay between two landlineLandline
A landline was originally an overland telegraph wire, as opposed to an undersea cable. Currently, landline refers to a telephone line which travels through a solid medium, either metal wire or optical fibre, as distinguished from a mobile cellular line, where transmission is via radio waves...
s being used for stereophonic sound
Stereophonic sound
The term Stereophonic, commonly called stereo, sound refers to any method of sound reproduction in which an attempt is made to create an illusion of directionality and audible perspective...
broadcasts. This application requires that the filter has a linear phase
Linear phase
Linear phase is a property of a filter, where the phase response of the filter is a linear function of frequency, excluding the possibility of wraps at \pm\pi. In a causal system, perfect linear phase can be achieved with a discrete-time FIR filter...
response with frequency (i.e., constant group delay
Group delay
Group delay is a measure of the time delay of the amplitude envelopes of the various sinusoidal components of a signal through a device under test, and is a function of frequency for each component...
) over a wide bandwidth and is the reason for choosing this topology.
Digital Implementation
A Z-transformZ-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
implementation of an all-pass filter with a complex pole at
iswhich has a zero at
, where denotes the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
. The pole and zero sit at the same angle but have reciprocal magnitudes (i.e., they are reflections of each other across the boundary of the complex
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
). The placement of this pole-zero pair for a given
can be rotated in the complex plane by any angle and retain its all-pass magnitude characteristic. Complex pole-zero pairs in all-pass filters help control the frequency where phase shifts occur.To create an all-pass implementation with real coefficients, the complex all-pass filter can be cascaded with an all-pass that substitutes
for , leading to the Z-transformZ-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
implementation
which is equivalent to the difference equation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
where
is the output and is the input at discrete time step .Filters such as the above can be cascaded with unstable or mixed-phase filters to create a stable or minimum-phase filter without changing the magnitude response of the system. For example, by proper choice of
, a pole of an unstable system that is outside of the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
can be canceled and reflected inside the unit circle.
See also
- Bridged T delay equaliserBridged T delay equaliserthumbThe bridged-T delay equaliser is an electrical all-pass filter circuit utilising bridged-T topology whose purpose is to insert an, ideally, constant delay at all frequencies in the signal path. It is a class of image filter.-Applications:...
- Lattice phase equaliserLattice phase equaliserA lattice phase equaliser or lattice filter is an example of an all-pass filter. That is, the attenuation of the filter is constant at all frequencies but the relative phase between input and output varies with frequency...
- Minimum phaseMinimum phaseIn control theory and signal processing, a linear, time-invariant system is said to be minimum-phase if the system and its inverse are causal and stable....
- Hilbert transformHilbert transformIn mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
- High-pass filterHigh-pass filterA high-pass filter is a device that passes high frequencies and attenuates frequencies lower than its cutoff frequency. A high-pass filter is usually modeled as a linear time-invariant system...
- Low-pass filterLow-pass filterA low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
- Band-stop filterBand-stop filterIn signal processing, a band-stop filter or band-rejection filter is a filter that passes most frequencies unaltered, but attenuates those in a specific range to very low levels. It is the opposite of a band-pass filter...
- Band-pass filterBand-pass filterA band-pass filter is a device that passes frequencies within a certain range and rejects frequencies outside that range.Optical band-pass filters are of common usage....
External links
- JOS@Stanford on all-pass filters
- ECE 209 Phase-Shifter Circuit — Analysis steps for a common analog phase-shifter circuit.