Image impedance
Encyclopedia
Image impedance is a concept used in electronic network design and analysis and most especially in filter design. The term image impedance applies to the impedance seen looking in to the port
s of a network. Usually a two-port network is implied but the concept is capable of being extended to networks with more than two ports. The definition of image impedance for a two-port network is the impedance, Zi 1, seen looking in to port 1 when port 2 is terminated with the image impedance, Zi 2, for port 2. In general, the image impedances of ports 1 and 2 will not be equal unless the network is symmetrical (or anti-symmetrical) with respect to the ports.
, Z, and a shunt admittance
, Y.
The difficulty here is that in order to find Zi 1 it is first necessary to terminate port 2 with Zi 2. However, Zi 2 is also an unknown at this stage. The problem is solved by terminating port 2 with an identical network: port 2 of the second network is connected to port 2 of the first network and port 1 of the second network is terminated with Zi 1. The second network is terminating the first network in Zi 2 as required. Mathematically, this is equivalent to eliminating one variable from a set of simultaneous equations. The network can now be solved for Zi 1. Writing out the expression for input impedance gives;
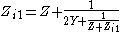
and solving for Zi 1,
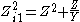
Zi 2 is found by a similar process, but it is simpler to work in terms of the reciprocal, that is image admittance Yi 2,
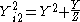
Also, it can be seen from these expressions that the two image impedances are related to each other by;
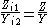
used in the analysis of transmission lines. In fact, in the limiting case of a chain of cascaded networks where the size of each single network is approaching an infinitesimally small element, the mathematical limit
of the image impedance expression is the characteristic impedance of the chain. That is,
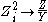
The connection between the two can further be seen by noting an alternative, but equivalent, definition of image impedance. In this definition, the image impedance of a network is the input impedance of an infinitely long chain of cascaded identical networks (with the ports arranged so that like impedance faces like). This is directly analogous to the definition of characteristic impedance as the input impedance of an infinitely long line.
Conversely, it is possible to analyse a transmission line with lumped
components, such as one utilising loading coils, in terms of an image impedance filter.
of the half section, like the image impedance, is calculated for a network terminated in its image impedances (or equivalently, as a section in an infinitely long chain of identical sections) and is given by,
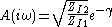
where γ is called the transmission function, propagation function or transmission parameter and is given by,
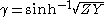
The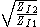
term represents the voltage ratio that would be observed if the maximum available power was transferred
from the source to the load. It would be possible to absorb this term into the definition of γ, and in some treatments this approach is taken. The purpose of separating it out is to scale γ so that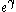
the actual voltage ratio may be. In the case of a network with symmetrical image impedances, such as a chain of an even number of identical L sections, the expression reduces to,
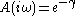
In general, γ is a complex number such that,
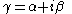
The real part of γ, represents an attenuation parameter, α in nepers and the imaginary part represents a phase change parameter, β in radians. The transmission parameters for a chain of n half sections, provided that like impedance always faces like, is given by;
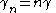
As with the image impedance, the transmission parameters approach those of a transmission line as the filter section become infinitesimally small so that,
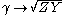
with α, β, γ, Z and Y all now being measured per metre instead of per half section.
Two-port network
A two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
s of a network. Usually a two-port network is implied but the concept is capable of being extended to networks with more than two ports. The definition of image impedance for a two-port network is the impedance, Zi 1, seen looking in to port 1 when port 2 is terminated with the image impedance, Zi 2, for port 2. In general, the image impedances of ports 1 and 2 will not be equal unless the network is symmetrical (or anti-symmetrical) with respect to the ports.
Derivation
As an example, the derivation of the image impedances of a simple 'L' network is given below. The L network consists of a series impedanceElectrical impedance
Electrical impedance, or simply impedance, is the measure of the opposition that an electrical circuit presents to the passage of a current when a voltage is applied. In quantitative terms, it is the complex ratio of the voltage to the current in an alternating current circuit...
, Z, and a shunt admittance
Admittance
In electrical engineering, the admittance is a measure of how easily a circuit or device will allow a current to flow. It is defined as the inverse of the impedance . The SI unit of admittance is the siemens...
, Y.
The difficulty here is that in order to find Zi 1 it is first necessary to terminate port 2 with Zi 2. However, Zi 2 is also an unknown at this stage. The problem is solved by terminating port 2 with an identical network: port 2 of the second network is connected to port 2 of the first network and port 1 of the second network is terminated with Zi 1. The second network is terminating the first network in Zi 2 as required. Mathematically, this is equivalent to eliminating one variable from a set of simultaneous equations. The network can now be solved for Zi 1. Writing out the expression for input impedance gives;
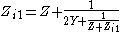
and solving for Zi 1,
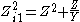
Zi 2 is found by a similar process, but it is simpler to work in terms of the reciprocal, that is image admittance Yi 2,
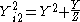
Also, it can be seen from these expressions that the two image impedances are related to each other by;
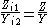
Usage in filter design
When used in filter design, the 'L' network analysed above is usually referred to as a half section. Two half sections in cascade will make either a T section or a Π section depending on which port of the L section comes first. This leads to the terminology of Zi T to mean the Zi 1 in the above analysis and Zi Π to mean Zi 2.Relation to characteristic impedance
Image impedance is a similar concept to the characteristic impedanceCharacteristic impedance
The characteristic impedance or surge impedance of a uniform transmission line, usually written Z_0, is the ratio of the amplitudes of a single pair of voltage and current waves propagating along the line in the absence of reflections. The SI unit of characteristic impedance is the ohm...
used in the analysis of transmission lines. In fact, in the limiting case of a chain of cascaded networks where the size of each single network is approaching an infinitesimally small element, the mathematical limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
of the image impedance expression is the characteristic impedance of the chain. That is,
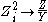
The connection between the two can further be seen by noting an alternative, but equivalent, definition of image impedance. In this definition, the image impedance of a network is the input impedance of an infinitely long chain of cascaded identical networks (with the ports arranged so that like impedance faces like). This is directly analogous to the definition of characteristic impedance as the input impedance of an infinitely long line.
Conversely, it is possible to analyse a transmission line with lumped
Lumped element model
The lumped element model simplifies the description of the behaviour of spatially distributed physical systems into a topology consisting of discrete entities that approximate the behaviour of the distributed system under certain assumptions...
components, such as one utilising loading coils, in terms of an image impedance filter.
Transfer function
The transfer functionTransfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
of the half section, like the image impedance, is calculated for a network terminated in its image impedances (or equivalently, as a section in an infinitely long chain of identical sections) and is given by,
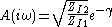
where γ is called the transmission function, propagation function or transmission parameter and is given by,
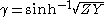
The
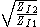term represents the voltage ratio that would be observed if the maximum available power was transferredMaximum power theorem
In electrical engineering, the maximum power transfer theorem states that, to obtain maximum external power from a source with a finite internal resistance, the resistance of the load must be equal to the resistance of the source as viewed from the output terminals...
from the source to the load. It would be possible to absorb this term into the definition of γ, and in some treatments this approach is taken. The purpose of separating it out is to scale γ so that
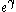the actual voltage ratio may be. In the case of a network with symmetrical image impedances, such as a chain of an even number of identical L sections, the expression reduces to,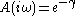In general, γ is a complex number such that,
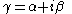
The real part of γ, represents an attenuation parameter, α in nepers and the imaginary part represents a phase change parameter, β in radians. The transmission parameters for a chain of n half sections, provided that like impedance always faces like, is given by;
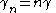
As with the image impedance, the transmission parameters approach those of a transmission line as the filter section become infinitesimally small so that,
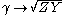
with α, β, γ, Z and Y all now being measured per metre instead of per half section.