
Lerch zeta function
Encyclopedia
In mathematics
, the Lerch zeta-function, sometimes called the Hurwitz–Lerch zeta-function, is a special function that generalizes the Hurwitz zeta-function and the polylogarithm. It is named after Mathias Lerch
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Lerch.html.
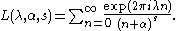
A related function, the Lerch transcendent, is given by
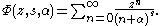
The two are related, as

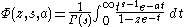
for

A contour integral representation is given by
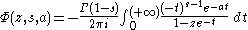
for
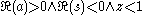
where the contour must not enclose any of the points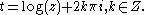
A Hermite-like integral representation is given by
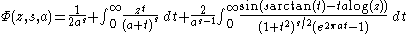
for
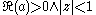
and
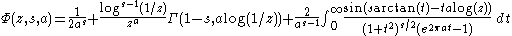
for
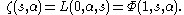
The polylogarithm is a special case of the Lerch Zeta, given by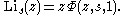
The Legendre chi function is a special case, given by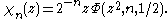
The Riemann zeta-function is given by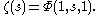
The Dirichlet eta-function is given by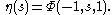
, and thus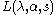 may be expressed as a finite sum over the Hurwitz zeta-function.
may be expressed as a finite sum over the Hurwitz zeta-function.
Various identities include: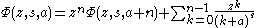
and
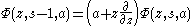
and
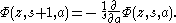

The series is valid for all s, and for complex z with Re(z)<1/2. Note a general resemblance to a similar series representation for the Hurwitz zeta function.
A Taylor's series in the first parameter was given by Erdélyi
. It may be written as the following series, which is valid for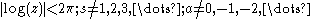
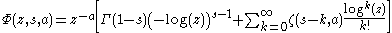
Please see:
B. R. Johnson,
Generalized Lerch zeta-function.
Pacific J. Math. 53, no. 1 (1974), 189–193.
http://projecteuclid.org/Dienst/UI/1.0/Display/euclid.pjm/1102911791?abstract=
If s is a positive integer, then
A Taylor series
in the third variable is given by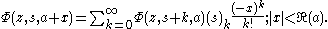
Series at a = -n is given by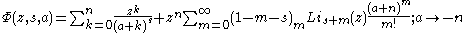
A special case for n = 0 has the following series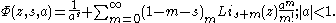
An asymptotic series for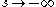
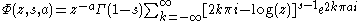
for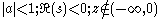
and
for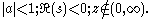
An asymptotic series in the incomplete Gamma function
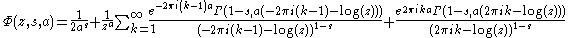
for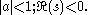
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lerch zeta-function, sometimes called the Hurwitz–Lerch zeta-function, is a special function that generalizes the Hurwitz zeta-function and the polylogarithm. It is named after Mathias Lerch
Mathias Lerch
Mathias Lerch was an eminent Czech mathematician who published about 250 papers, largely on mathematical analysis and number theory...
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Lerch.html.
Definition
The Lerch zeta-function is given by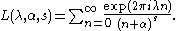
A related function, the Lerch transcendent, is given by
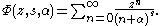
The two are related, as

Integral representations
An integral representation is given by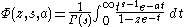
for

A contour integral representation is given by
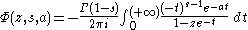
for
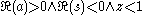
where the contour must not enclose any of the points
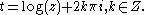
A Hermite-like integral representation is given by
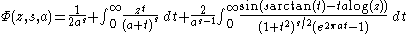
for
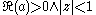
and
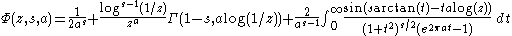
for

Special cases
The Hurwitz zeta-function is a special case, given by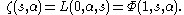
The polylogarithm is a special case of the Lerch Zeta, given by
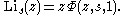
The Legendre chi function is a special case, given by
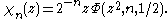
The Riemann zeta-function is given by
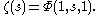
The Dirichlet eta-function is given by
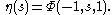
Identities
For λ rational, the summand is a root of unityRoot of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, and thus
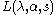 may be expressed as a finite sum over the Hurwitz zeta-function.
may be expressed as a finite sum over the Hurwitz zeta-function.Various identities include:
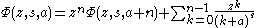
and
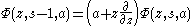
and
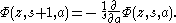
Series representations
A series representation for the Lerch transcendent is given by
The series is valid for all s, and for complex z with Re(z)<1/2. Note a general resemblance to a similar series representation for the Hurwitz zeta function.
A Taylor's series in the first parameter was given by Erdélyi
Arthur Erdélyi
Arthur Erdélyi FRS, FRSE was a Hungarian-born British mathematician. Erdélyi was a leading expert on special functions - especially orthogonal polynomials and hypergeometric functions.-Biography:...
. It may be written as the following series, which is valid for
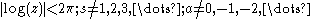
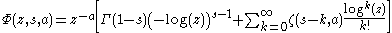
- (the correctness of this formula is disputed, please see the talk page)
Please see:
B. R. Johnson,
Generalized Lerch zeta-function.
Pacific J. Math. 53, no. 1 (1974), 189–193.
http://projecteuclid.org/Dienst/UI/1.0/Display/euclid.pjm/1102911791?abstract=
If s is a positive integer, then

A Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
in the third variable is given by
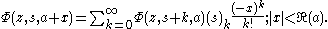
Series at a = -n is given by
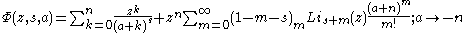
A special case for n = 0 has the following series
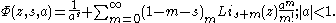
An asymptotic series for
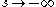
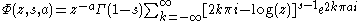
for
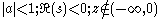
and

for
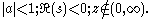
An asymptotic series in the incomplete Gamma function
Incomplete gamma function
In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
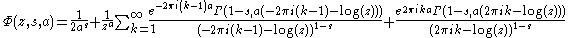
for
External links
.- Ramunas Garunkstis, Home Page (2005) (Provides numerous references and preprints.)
- Ramunas Garunkstis, Approximation of the Lerch Zeta Function (PDF)
- S. Kanemitsu, Y. Tanigawa and H. Tsukada, A generalization of Bochner's formula, (undated, 2005 or earlier)

