
Zeta function (operator)
Encyclopedia
The zeta function of a mathematical operator  is a function defined as
is a function defined as

for those values of s where this expression exists, and as an analytic continuation
thereof for those values of s where it does not. Here "tr" denotes a functional trace
.
The zeta function may also be expressible in terms of the eigenvalues of the operator
of the operator  by
by
 .
.
It is used in giving a rigorous definition to the functional determinant
of an operator, which is given by
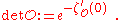
The Minakshisundaram–Pleijel zeta function is an example, when the operator is the Laplacian of a compact Riemannian manifold.
 is a function defined as
is a function defined as
for those values of s where this expression exists, and as an analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
thereof for those values of s where it does not. Here "tr" denotes a functional trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
.
The zeta function may also be expressible in terms of the eigenvalues
 of the operator
of the operator  by
by .
.It is used in giving a rigorous definition to the functional determinant
Functional determinant
In mathematics, if S is a linear operator mapping a function space V to itself, it is sometimes possible to define an infinite-dimensional generalization of the determinant. The corresponding quantity det is called the functional determinant of S.There are several formulas for the functional...
of an operator, which is given by
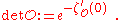
The Minakshisundaram–Pleijel zeta function is an example, when the operator is the Laplacian of a compact Riemannian manifold.

