Motivic zeta function
Encyclopedia
In algebraic geometry
, the motivic zeta function of a smooth algebraic variety
is the formal power series
Here
is the 
-th symmetric power of 
, i.e., the quotient of 
by the action of the symmetric group
, and 
is the class of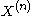 
in the ring of motives (see below).
If the ground field
is finite, and one applies the counting measure to
, one obtains the local zeta function of 
.
If the ground field is the complex numbers, and one applies Euler characteristic
with compact supports to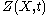
, one obtains 
.
from the set of finite type schemes
over a field
to a commutative ring
, satisfying the three properties
depends only on the isomorphism class of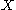 
,
if 
is a closed subscheme of 
,
.
For example if
is a finite field and 
is the ring of integers, then 
defines a motivic measure, the counting measure.
If the ground field is the complex numbers, then Euler characteristic with compact supports defines a motivic measure with values in the integers.
The zeta function with respect to a motivic measure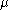
is the formal power series in 
given by
.
There is a universal motivic measure. It takes values in the K-ring of varieties,
, which is the ring generated by the symbols 
, for all varieties 
, subject to the relations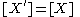
if 
and 
are isomorphic,
if 
is a closed subvariety of 
,
.
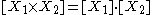The universal motivic measure gives rise to the motivic zeta function.
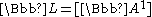denote the class of the affine line
.
If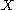
is a smooth projective irreducible curve
of genus
admitting a line bundle
of degree 1, and the motivic measure takes values in a field in which
is invertible, then
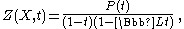
where
is a polynomial of degree 
. Thus, in this case, the motivic zeta function is rational
. In higher dimension, the motivic zeta function is not always rational.
If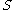
is a smooth surface
over an algebraically closed field of characteristic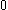
, then the generating function for the motives of the Hilbert schemes
of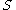
can be expressed in terms of the motivic zeta function by Göttsche's
Formula
Here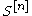
is the Hilbert scheme of length 
subschemes of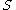 
. For the affine plane this formula gives
This is essentially the partition function.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the motivic zeta function of a smooth algebraic variety
Abstract variety
In mathematics, in the field of algebraic geometry, the idea of abstract variety is to define a concept of algebraic variety in an intrinsic way. This followed the trend in the definition of manifold independent of any ambient space by some years, the first notions being those of Oscar Zariski and...
is the formal power seriesFormal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
Here
is the -th symmetric power of , i.e., the quotient of by the action of the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
, and is the class of 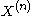in the ring of motives (see below).If the ground field
Ground field
In mathematics, a ground field is a field K fixed at the beginning of the discussion. It is used in various areas of algebra: for example in linear algebra where the concept of a vector space may be developed over any field; and in algebraic geometry, where in the foundational developments of André...
is finite, and one applies the counting measure to
, one obtains the local zeta function of .If the ground field is the complex numbers, and one applies Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
with compact supports to
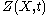, one obtains .Motivic measures
A motivic measure is a map from the set of finite type schemesScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
to a commutative ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, satisfying the three properties depends only on the isomorphism class of 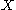, if is a closed subscheme of ,.For example if
is a finite field and is the ring of integers, then defines a motivic measure, the counting measure.If the ground field is the complex numbers, then Euler characteristic with compact supports defines a motivic measure with values in the integers.
The zeta function with respect to a motivic measure
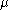is the formal power series in given by.There is a universal motivic measure. It takes values in the K-ring of varieties,
, which is the ring generated by the symbols , for all varieties , subject to the relations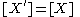 if and are isomorphic, if is a closed subvariety of ,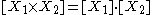.The universal motivic measure gives rise to the motivic zeta function.
Examples
Let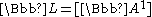 denote the class of the affine lineAffine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
.
If
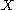is a smooth projective irreducible curveAlgebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of genus
admitting a line bundleLine bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
of degree 1, and the motivic measure takes values in a field in which
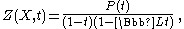
is invertible, thenwhere
is a polynomial of degree . Thus, in this case, the motivic zeta function is rationalRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
. In higher dimension, the motivic zeta function is not always rational.
If
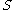is a smooth surfaceSurface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
over an algebraically closed field of characteristic
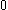, then the generating function for the motives of the Hilbert schemesHilbert scheme
In algebraic geometry, a branch of mathematics, a Hilbert scheme is a scheme that is the parameter space for the closed subschemes of some projective space , refining the Chow variety. The Hilbert scheme is a disjoint union of projective subschemes corresponding to Hilbert polynomials...
of
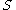can be expressed in terms of the motivic zeta function by Göttsche'sLothar Göttsche
Lothar Göttsche is a German mathematician, known for his work in algebraic geometry. After studying mathematics at the University of Kiel, he received his Dr. rer. nat. under the direction of Friedrich Hirzebruch at the University of Bonn in 1989. He was invited as speaker to the International...
Formula
Here
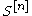is the Hilbert scheme of length subschemes of 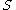. For the affine plane this formula givesThis is essentially the partition function.