Prime zeta function
Encyclopedia
In mathematics
, the Prime zeta function is an analogue of the Riemann zeta function, studied by . It is defined as the following infinite series, which converges for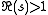
:
.
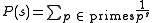The Euler product
for the Riemann zeta function ζ(s) implies that
which by Möbius inversion gives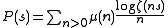
When s goes to 1, we have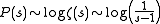
.
This is used in the definition of Dirichlet density
.
This gives the continuation of P(s) to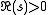
, with an infinite number of logarithmic singularities at points where ns is a pole or zero of ζ(s). The line 
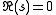is a natural boundary as the singularities cluster near all points of this line.
If we define a sequence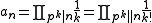
then
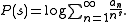
(Exponentiation shows that this is equivalent to Lemma 2.7 by Li.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Prime zeta function is an analogue of the Riemann zeta function, studied by . It is defined as the following infinite series, which converges for
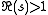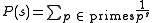:.The Euler product
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
for the Riemann zeta function ζ(s) implies that
which by Möbius inversion gives
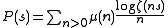
When s goes to 1, we have
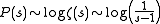.This is used in the definition of Dirichlet density
Dirichlet density
In mathematics, the Dirichlet density of a set of primes, named after Johann Gustav Dirichlet, is a measure of the size of the set that is easier to use than the natural density.-Definition:...
.
This gives the continuation of P(s) to
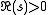, with an infinite number of logarithmic singularities at points where ns is a pole or zero of ζ(s). The line 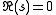is a natural boundary as the singularities cluster near all points of this line.If we define a sequence
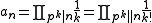
then
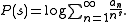
(Exponentiation shows that this is equivalent to Lemma 2.7 by Li.)