Partition (number theory)
Encyclopedia
In number theory
and combinatorics
, a partition of a positive integer
n, also called an integer partition, is a way of writing n as a sum
of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a composition
. For example, 4 can be partitioned in five distinct ways:
The order-dependent composition 1 + 3 is the same partition as 3 + 1, while 1 + 2 + 1 and 1 + 1 + 2 are the same partition as 2 + 1 + 1.
A summand in a partition is also called a part. The number of partitions of n is given by the partition function p(n). The notation p n means that p is a partition of n. So p(4) = 5.
Partitions can be graphically visualized with Young diagrams or Ferrers diagrams. They occur in a number of branches of mathematics
and physics
, including the study of symmetric polynomial
s, the symmetric group
and in group representation theory
in general.
In some sources partitions are treated as the sequence of summands, rather than as an expression with plus signs. For example, the partition 2 + 1 + 1 might instead be written as the tuple or in the even more compact form where the superscript indicates the number of repetitions of a term.
, the partition function p(n) represents the number
of possible partitions of a natural number n, which is to say the number of distinct (and order independent) ways of representing n as a sum
of natural numbers. By convention p(0) = 1, p(n) = 0 for n negative.
There are 190,569,292 partitions of the number 100, and approximately 2.4 partitions of the number 1000.
, the largest known prime number
that counts a number of partitions is p(60016427), with 8622 decimal digits, found by Bernardo Boncompagni.
The number of partitions meeting the first condition is p(k, n − k). To see this, imagine a list of all the partitions of the number n − k into numbers of size at least k, then imagine appending "+ k" to each partition in the list. Now what is it a list of?
As a side note, one can use this to define a sort of recursion relation for the partition function in term of the intermediate function, namely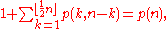
where
is the floor function
.
The number of partitions meeting the second condition is p(k + 1, n) since a partition into parts of at least k that contains no parts of exactly k must have all parts at least k + 1.
Since the two conditions are mutually exclusive
, the number of partitions meeting either condition is p(k + 1, n) + p(k, n − k). The recursively defined
function is thus:
This function tends to exhibit deceptive behavior.
Our original function p(n) is just p(1, n).
The values of this function:
for p(n) is given by the reciprocal of Euler's function:
Expanding each term on the right-hand side as a geometric series, we can rewrite it as
(1 + x2 + x4 + x6 + ...)(1 + x3 + x6 + x9 + ...) ....
The xn term in this product counts the number of ways to write
where each number i appears ai times. This is precisely the definition of a partition of n, so our product is the desired generating function. More generally, the generating function for the partitions of n into numbers from a set A can be found by taking only those terms in the product where k is an element of A. This result is due to Euler
.
The formulation of Euler's generating function is a special case of a q-Pochhammer symbol and is similar to the product formulation of many modular form
s, and specifically the Dedekind eta function
. It can also be used in conjunction with the pentagonal number theorem to derive a recurrence for the partition function stating that:
where p(0) is taken to equal 1, p(k) is zero for negative k, and the sum is taken over all generalized pentagonal numbers
of the form ½n(3n − 1), for n running over positive and negative integers: successively taking n = 1, −1, 2, −2, 3, −3, 4, −4 ..., generates the values 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, .... The signs in the summation continue to alternate +, +, −, −, +, +, ...
is credited with discovering that "congruences" in the number of partitions exist for integers ending in 4 and 9.
For instance, the number of partitions for the integer 4 is 5. For the integer 9, the number of partitions is 30; for 14 there are 135 partitions. He also discovered congruences related to 7 and 11:
Since 5, 7, and 11 are consecutive primes
, one might think that there would be such a congruence for the next prime 13,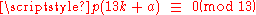
for some a. This is, however, false. It can also be shown that there is no congruence of the form 
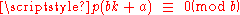for any prime b other than 5, 7, or 11.
In the 1960s, A. O. L. Atkin
of the University of Illinois at Chicago
discovered additional congruences for small prime moduli. For example: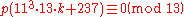
In 2000, Ken Ono
of the University of Wisconsin–Madison
proved that there are such congruences for every prime modulus. A few years later Ono, together with Scott Ahlgren of the University of Illinois, proved that there are partition congruences modulo every integer coprime to 6.
expression for p(n) is given by
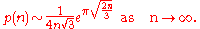
This asymptotic formula
was first obtained by G. H. Hardy
and Ramanujan in 1918 and independently by J. V. Uspensky
in 1920. Considering p(1000), the asymptotic formula gives about 2.4402 × 1031, reasonably close to the exact answer given above (1.415% larger than the true value).
In 1937, Hans Rademacher
was able to improve on Hardy and Ramanujan's results by providing a convergent series expression for p(n). It is
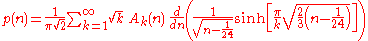
where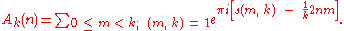
It can be shown that the derivative part of the sum can be simplified. Here, the notation (m, n) = 1 implies that the sum should occur only over the values of m that are relatively prime to n. The function s(m, k) is a Dedekind sum
. The proof of Rademacher's formula involves Ford circle
s, Farey sequence
s, modular symmetry
and the Dedekind eta function
in a central way.
In January 2011, it was announced that Ono and Jan Hendrik Bruinier, of the Technische Universität Darmstadt, had developed a finite, algebraic formula determining the value of p(n) for any positive integer n.
The partition function can be expressed as a sum over the pentagonal partitions of n. Let n = k1 + 2k2 + 5k5 + . . . =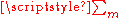
q m kqm be a pentagonal partition of n, where each qm = m(3m-1)/2 is a generalized pentagonal number
(GPN) with qM being the largest GPN less than or equal to n. Then
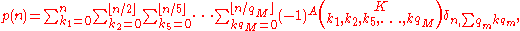
where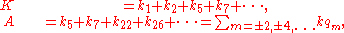
and where
is a multinomial coefficient. The number of terms in the sum for p(n) is sequence . E.g., 8=7+1 = 5+2+1 = 5+1+1+1 = 2+2+2+2 = . . . . , and
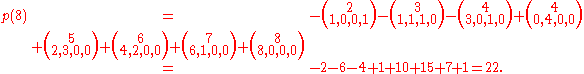
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, a partition of a positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n, also called an integer partition, is a way of writing n as a sum
SUM
SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a composition
Composition (number theory)
In mathematics, a composition of an integer n is a way of writing n as the sum of a sequence of positive integers. Two sequences that differ in the order of their terms define different compositions of their sum, while they are considered to define the same partition of that number. Any integer...
. For example, 4 can be partitioned in five distinct ways:
- 4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1.
The order-dependent composition 1 + 3 is the same partition as 3 + 1, while 1 + 2 + 1 and 1 + 1 + 2 are the same partition as 2 + 1 + 1.
A summand in a partition is also called a part. The number of partitions of n is given by the partition function p(n). The notation p n means that p is a partition of n. So p(4) = 5.
Partitions can be graphically visualized with Young diagrams or Ferrers diagrams. They occur in a number of branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, including the study of symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s, the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
and in group representation theory
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
in general.
Examples
The partitions of 4 are:- 4
- 3 + 1
- 2 + 2
- 2 + 1 + 1
- 1 + 1 + 1 + 1
In some sources partitions are treated as the sequence of summands, rather than as an expression with plus signs. For example, the partition 2 + 1 + 1 might instead be written as the tuple or in the even more compact form where the superscript indicates the number of repetitions of a term.
Partition function
In number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the partition function p(n) represents the number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
of possible partitions of a natural number n, which is to say the number of distinct (and order independent) ways of representing n as a sum
SUM
SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
of natural numbers. By convention p(0) = 1, p(n) = 0 for n negative.
Values
The number of partitions of the numbers from 1 to 10 are- 1, 2, 3, 5, 7, 11, 15, 22, 30, 42 .
There are 190,569,292 partitions of the number 100, and approximately 2.4 partitions of the number 1000.
, the largest known prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
that counts a number of partitions is p(60016427), with 8622 decimal digits, found by Bernardo Boncompagni.
Intermediate function
One way of getting a handle on the partition function involves an intermediate function p(k, n), which represents the number of partitions of n using only natural numbers at least as large as k. For any given value of k, partitions counted by p(k, n) fit into exactly one of the following categories:- smallest addend is k
- smallest addend is strictly greater than k.
The number of partitions meeting the first condition is p(k, n − k). To see this, imagine a list of all the partitions of the number n − k into numbers of size at least k, then imagine appending "+ k" to each partition in the list. Now what is it a list of?
As a side note, one can use this to define a sort of recursion relation for the partition function in term of the intermediate function, namely
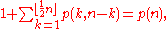
where
is the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
.
The number of partitions meeting the second condition is p(k + 1, n) since a partition into parts of at least k that contains no parts of exactly k must have all parts at least k + 1.
Since the two conditions are mutually exclusive
Mutually exclusive
In layman's terms, two events are mutually exclusive if they cannot occur at the same time. An example is tossing a coin once, which can result in either heads or tails, but not both....
, the number of partitions meeting either condition is p(k + 1, n) + p(k, n − k). The recursively defined
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
function is thus:
- p(k, n) = 0 if k > n
- p(k, n) = 1 if k = n
- p(k, n) = p(k+1, n) + p(k, n − k) otherwise.
This function tends to exhibit deceptive behavior.
- p(1, 4) = 5
- p(2, 8) = 7
- p(3, 12) = 9
- p(4, 16) = 11
- p(5, 20) = 13
- p(6, 24) = 16
Our original function p(n) is just p(1, n).
The values of this function:
| k | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| n | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 3 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 5 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5 | 7 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 6 | 11 | 4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 7 | 15 | 4 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |
| 8 | 22 | 7 | 3 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 9 | 30 | 8 | 4 | 2 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 10 | 42 | 12 | 5 | 3 | 2 | 1 | 1 | 1 | 1 | 1 |
Generating function
A generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for p(n) is given by the reciprocal of Euler's function:
Expanding each term on the right-hand side as a geometric series, we can rewrite it as
(1 + x2 + x4 + x6 + ...)(1 + x3 + x6 + x9 + ...) ....
The xn term in this product counts the number of ways to write
- n = a1 + 2a2 + 3a3 + ... = (1 + 1 + ... + 1) + (2 + 2 + ... + 2) + (3 + 3 + ... + 3) + ...,
where each number i appears ai times. This is precisely the definition of a partition of n, so our product is the desired generating function. More generally, the generating function for the partitions of n into numbers from a set A can be found by taking only those terms in the product where k is an element of A. This result is due to Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
.
The formulation of Euler's generating function is a special case of a q-Pochhammer symbol and is similar to the product formulation of many modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s, and specifically the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
. It can also be used in conjunction with the pentagonal number theorem to derive a recurrence for the partition function stating that:
- p(k) = p(k − 1) + p(k − 2) − p(k − 5) − p(k − 7) + p(k − 12) + p(k − 15) − p(k − 22) − ...
where p(0) is taken to equal 1, p(k) is zero for negative k, and the sum is taken over all generalized pentagonal numbers
Pentagonal number
A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical...
of the form ½n(3n − 1), for n running over positive and negative integers: successively taking n = 1, −1, 2, −2, 3, −3, 4, −4 ..., generates the values 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, .... The signs in the summation continue to alternate +, +, −, −, +, +, ...
Congruences
Srinivasa RamanujanSrinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
is credited with discovering that "congruences" in the number of partitions exist for integers ending in 4 and 9.
For instance, the number of partitions for the integer 4 is 5. For the integer 9, the number of partitions is 30; for 14 there are 135 partitions. He also discovered congruences related to 7 and 11:
Since 5, 7, and 11 are consecutive primes
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, one might think that there would be such a congruence for the next prime 13,
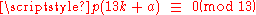for some a. This is, however, false. It can also be shown that there is no congruence of the form 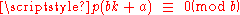for any prime b other than 5, 7, or 11.In the 1960s, A. O. L. Atkin
A. O. L. Atkin
Arthur Oliver Lonsdale Atkin , who published under the name A. O. L. Atkin, was a Professor Emeritus of mathematics at the University of Illinois at Chicago. As an undergraduate during World War II, he worked at Bletchley Park cracking German codes. He received his Ph.D...
of the University of Illinois at Chicago
University of Illinois at Chicago
The University of Illinois at Chicago, or UIC, is a state-funded public research university located in Chicago, Illinois, United States. Its campus is in the Near West Side community area, near the Chicago Loop...
discovered additional congruences for small prime moduli. For example:
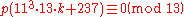
In 2000, Ken Ono
Ken Ono
Ken Ono is an American mathematician who specializes in number theory, especially in integer partitions, modular forms, and the fields of interest to Srinivasa Ramanujan...
of the University of Wisconsin–Madison
University of Wisconsin–Madison
The University of Wisconsin–Madison is a public research university located in Madison, Wisconsin, United States. Founded in 1848, UW–Madison is the flagship campus of the University of Wisconsin System. It became a land-grant institution in 1866...
proved that there are such congruences for every prime modulus. A few years later Ono, together with Scott Ahlgren of the University of Illinois, proved that there are partition congruences modulo every integer coprime to 6.
Partition function formulas
An asymptoticAsymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
expression for p(n) is given by
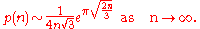
This asymptotic formula
Asymptotic formula
In mathematics, an asymptotic formula for a quantity depending on natural numbers, or on a variable taking real numbers as values, is a function of natural numbers, or of a real variable, whose values are nearly equal to the values of the former when both are evaluated for the same large values...
was first obtained by G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and Ramanujan in 1918 and independently by J. V. Uspensky
J. V. Uspensky
James Victor Uspensky was a mathematician who wrote Theory of Equations.He graduated from the University of St. Petersburg in 1906 and received his doctorate from the University of St. Petersburg in 1910...
in 1920. Considering p(1000), the asymptotic formula gives about 2.4402 × 1031, reasonably close to the exact answer given above (1.415% larger than the true value).
In 1937, Hans Rademacher
Hans Rademacher
Hans Adolph Rademacher was a German mathematician, known for work in mathematical analysis and number theory.-Biography:...
was able to improve on Hardy and Ramanujan's results by providing a convergent series expression for p(n). It is
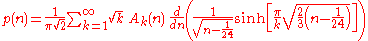
where
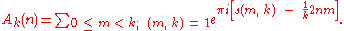
It can be shown that the derivative part of the sum can be simplified. Here, the notation (m, n) = 1 implies that the sum should occur only over the values of m that are relatively prime to n. The function s(m, k) is a Dedekind sum
Dedekind sum
In mathematics, Dedekind sums, named after Richard Dedekind, are certain sums of products of a sawtooth function, and are given by a function D of three integer variables. Dedekind introduced them to express the functional equation of the Dedekind eta function. They have subsequently been much...
. The proof of Rademacher's formula involves Ford circle
Ford circle
In mathematics, a Ford circle is a circle with centre at and radius 1/, where p/q is an irreducible fraction, i.e. p and q are coprime integers...
s, Farey sequence
Farey sequence
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
s, modular symmetry
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
and the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
in a central way.
In January 2011, it was announced that Ono and Jan Hendrik Bruinier, of the Technische Universität Darmstadt, had developed a finite, algebraic formula determining the value of p(n) for any positive integer n.
The partition function can be expressed as a sum over the pentagonal partitions of n. Let n = k1 + 2k2 + 5k5 + . . . =
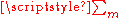q m kqm be a pentagonal partition of n, where each qm = m(3m-1)/2 is a generalized pentagonal numberPentagonal number
A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical...
(GPN) with qM being the largest GPN less than or equal to n. Then
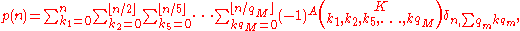
where
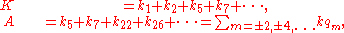
and where
is a multinomial coefficient. The number of terms in the sum for p(n) is sequence . E.g., 8=7+1 = 5+2+1 = 5+1+1+1 = 2+2+2+2 = . . . . , and
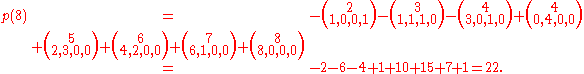
Determinant formulas
The value of p(n) for any n can be found from the formula:-
I.e., p(n) is the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the n X n truncation of the infinite-dimensional Toeplitz matrixToeplitz matrixIn linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...
shown above. The only non-zero diagonals of this matrix are those which start on a row labeled by a generalized pentagonal number qm. (The superdiagonal is taken to start on row "0".) On these diagonals, the matrix element is (-1)m+1. This determinant formula is equivalent to the matrix relation,
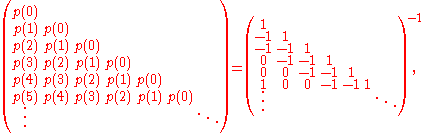
which is simply the generating-function equation above (plus the pentagonal number theorem) translated into matrix form.
By using the identity by Ramanujan,
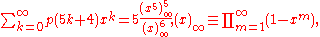
the partition function p(5k-1) can be expressed alternatively as the determinant of a lower, k-dimensional matrix:
The numbers making up the first column correspond to sequence , while every fifth element (after the initial "1") in the last column is from sequence : (1,-5,5,10,-15,-6, . . . .); all other elements in that column are zero. For example,
In a like fashion, by using two other identities by Ramanujan, the partition functions p(7k-2) and p(25k-1) can also be expressed as k-dimensional determinants:
where the first column in each matrix is sequence and , respectively, and the last column in each is from the expansions:
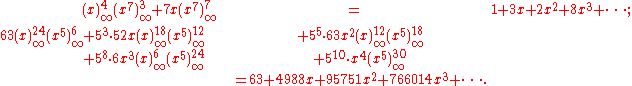
As an example, the calculation of p(149) is:
-
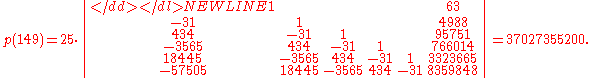
The nth partial sum of the partition function is given by
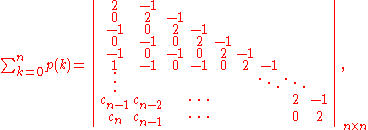
where c0 =-1, c1 = 2, c2 = 0, and for k > 2,
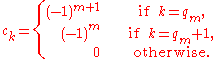
The partition function for partitions into distinct integers, q(n), is-
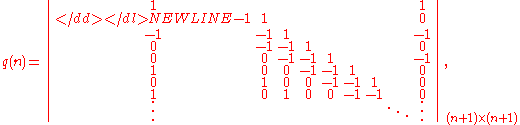
where the first column is sequence , and a matrix element in the last column equals (-1) m if the row number is 2qm+1; otherwise it equals zero. (This is also the partition function for partitions into odd integers; see below.)
Restricted partitions
Among the 22 partitions for the number 8, 6 contain
only odd parts:- 7 + 1
- 5 + 3
- 5 + 1 + 1 + 1
- 3 + 3 + 1 + 1
- 3 + 1 + 1 + 1 + 1 + 1
- 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
If we count the partitions of 8
with distinct parts, we also obtain the number 6:- 8
- 7 + 1
- 6 + 2
- 5 + 3
- 5 + 2 + 1
- 4 + 3 + 1
It is true for all positive numbers that the number of partitions with odd parts always equals the number of partitions with distinct parts. This result was proved by Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
in 1748.
Some similar results about restricted partitions can be obtained by the aid of a visual tool, a Ferrers graph (also called Ferrers diagram, since it is not a graph in the graph-theoreticalGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
sense, or sometimes Young diagram, alluding to the Young tableauYoung tableauIn mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
).
Ferrers diagram
The partition 6 + 4 + 3 + 1 of the positive number 14 can be represented
by the following diagram; these diagrams are named in honor of Norman Macleod FerrersNorman Macleod FerrersNorman Macleod Ferrers was a British mathematician and university administrator.-Life:Ferrers was educated at Eton College before studying at Gonville and Caius College, Cambridge, where he was Senior Wrangler in 1851. He was appointed to a Fellowship at the college in 1852, and was ordained in...
:
6 + 4 + 3 + 1
The 14 circles are lined up in 4 columns, each having the size of a part of the partition. The diagrams for the 5 partitions of the number 4 are listed below:
4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1
If we now flip the diagram of the partition 6 + 4 + 3 + 1 along its main diagonal, we obtain another partition of 14:
↔ 6 + 4 + 3 + 1 = 4 + 3 + 3 + 2 + 1 + 1
By turning the rows into columns, we obtain the partition 4 + 3 + 3 + 2 + 1 + 1 of the number 14. Such partitions are said to be conjugate of one another. In the case of the number 4, partitions 4 and 1 + 1 + 1 + 1 are conjugate pairs, and partitions 3 + 1 and 2 + 1 + 1 are conjugate of each other. Of particular interest is the partition 2 + 2, which has itself as conjugate. Such a partition is said to be self-conjugate.
Claim: The number of self-conjugate partitions is the same as the number of partitions with distinct odd parts.
Proof (outline): The crucial observation is that every odd part can be "folded" in the middle to form a self-conjugate diagram:
↔
One can then obtain a bijection between the set of partitions with distinct odd parts and the set of self-conjugate partitions, as illustrated by the following example:
↔ 9 + 7 + 3 = 5 + 5 + 4 + 3 + 2 Dist. odd self-conjugate
Similar techniques can be employed to establish, for example, the following equalities:- The number of partitions of n into no more than k parts is the same as the number of partitions of n into parts no larger than k.
- The number of partitions of n into no more than k parts is the same as the number of partitions of n + k into exactly k parts.
Young diagrams
An alternative visual representation of an integer partition is its Young diagram, named after the British mathematician Alfred YoungAlfred YoungAlfred Young, FRS was a British mathematician.He was born in Widnes, Lancashire, England and educated at Monkton Combe School in Somerset and Clare College, Cambridge, graduating BA as 10th Wrangler in 1895. He is known for his work in the area of group theory...
. Rather than representing a partition with dots, as in the Ferrers diagram, the Young diagram uses boxes. Thus, the Young diagram for the partition 5 + 4 + 1 is
while the Ferrers diagram for the same partition is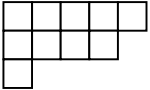
|- style="vertical-align:top; text-align:left;"
||- style="vertical-align:top; text-align:center;"
|}
While this seemingly trivial variation doesn't appear worthy of separate mention, Young diagrams turn out to be extremely useful in the study of symmetric functions and group representation theory: in particular, filling the boxes of Young diagrams with numbers (or sometimes more complicated objects) obeying various rules leads to a family of objects called Young tableaux, and these tableaux have combinatorial and representation-theoretic significance.
See also
- Young's latticeYoung's latticeIn mathematics, Young's lattice is a partially ordered set and a lattice that is formed by all integer partitions. It is named after Alfred Young, who in a series of papers On quantitative substitutional analysis developed representation theory of the symmetric group...
- Dominance orderDominance orderDominance order is a partial order on the set of partitions of a positive integer n that plays an important role in algebraic combinatorics and representation theory, especially in the context of symmetric functions and representation theory of the symmetric group.- Definition :If...
- Partition of a setPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
- Plane partition
- Polite numberPolite numberIn number theory, a polite number is a positive integer that can be written as the sum of two or more consecutive positive integers. Other positive integers are impolite....
, defined by partitions into consecutive integers - Multiplicative partitionMultiplicative partitionIn number theory, a multiplicative partition or unordered factorization of an integer n that is greater than 1 is a way of writing n as a product of integers greater than 1, treating two products as equivalent if they differ only in the ordering of the factors. The number n is itself considered one...
- Twelvefold wayTwelvefold wayIn combinatorics, the twelvefold way is a name given to a systematic classification of 12 related enumerative problems concerning two finite sets, which include the classical problems of counting permutations, combinations, multisets, and partitions either of a set or of a number...
- Ewens's sampling formulaEwens's sampling formulaIn population genetics, Ewens' sampling formula, describes the probabilities associated with counts of how many different alleles are observed a given number of times in the sample.-Definition:...
- Faà di Bruno's formulaFaà di Bruno's formulaFaà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives, named after , though he was not the first to state or prove the formula...
- MultisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
- Newton's identitiesNewton's identitiesIn mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
- Leibniz's distribution table for integer partitions
- Durfee squareDurfee squareIn number theory, a Durfee square is an attribute of an integer partition. A partition of n has a Durfee square of side s if s is the largest number such that the partition contains at least s parts with values ≥ s...
- Smallest-parts functionSpt functionThe spt function is a function in number theory that counts the sum of the number of smallest parts in each partition of a positive integer. It is related to the partition function....
External links
- Partition and composition calculator
- First 4096 values of the partition function
- An algorithm to compute the partition function
- Pieces of Number from Science News Online
- Lectures on Integer Partitions by Herbert S. Wilf
- Counting with partitions with reference tables to the On-Line Encyclopedia of Integer Sequences
- Integer::Partition Perl module from CPANCPANCPAN, the Comprehensive Perl Archive Network, is an archive of nearly 100,000 modules of software written in Perl, as well as documentation for it. It has a presence on the World Wide Web at and is mirrored worldwide at more than 200 locations...
- Fast Algorithms For Generating Integer Partitions
- Generating All Partitions: A Comparison Of Two Encodings
- Amanda Folsom, Zachary A. Kent, and Ken Ono, l-adic properties of the partition function. In press.
- Jan Hendrik Bruinier and Ken Ono, An algebraic formula for the partition function. In press.
-
-