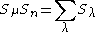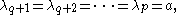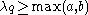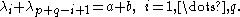Littlewood–Richardson rule
Encyclopedia
In mathematics
, the Littlewood–Richardson rule is a combinatorial description of the coefficients that arise when decomposing a product of two Schur functions
as a linear combination of other Schur functions. These coefficients are natural numbers, which the Littlewood–Richardson rule describes as counting certain skew tableaux. They occur in many other mathematical contexts, for instance as multiplicity in the decomposition of tensor product
s of irreducible representations of general linear group
s (or related groups like the special linear
and special unitary group
s), or in the decomposition of certain induced representations in the representation theory of the symmetric group
, or in the area of algebraic combinatorics
dealing with Young tableaux and symmetric polynomials
Littlewood–Richardson coefficients depend on three partitions, say
, of which 
and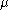 
describe the Schur functions being multiplied, and 
gives the Schur function of which this is the coefficient in the linear combination; in other words they are the coefficients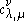 
such that
The Littlewood–Richardson rule states that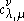
is equal to the number of Littlewood–Richardson tableaux of shape 
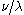and of weight 
.
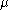claimed to complete their proof, but his argument had gaps, though it was so obscurely written that these gaps were not noticed for some time, and his argument is reproduced in the book . Some of the gaps were later filled by . The first rigorous proofs of the rule were given four decades after it was found, by and , after the necessary combinatorial theory was developed by , , and in their work on the Robinson–Schensted correspondence.
There are now several short proofs of the rule, such as , and using Bender-Knuth involutions.
used the Littelmann path model
to generalize the Littlewood–Richardson rule to other semisimple Lie groups.
The Littlewood–Richardson rule is notorious for the number of errors that appeared prior to its complete, published proof. Several published attempts to prove it are incomplete, and it is particularly difficult to avoid errors when doing hand calculations with it: even the original example in contains an error.
is equal to the number of Littlewood–Richardson tableaux of shape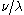 
and of weight 
.
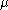-(2,1)_word_112123.svg.png)
A Littlewood–Richardson tableau is a skew semistandard tableau with the additional property that the sequence obtained by concatenating its reversed rows is a lattice word (or lattice permutation), which means that in every initial part of the sequence any number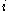 
occurs at least as often as the number 
. Another equivalent (though not quite obviously so) characterization is that the tableau itself, and any tableau obtained from it by removing some number of its leftmost columns, has a weakly decreasing weight. Many other combinatorial notions have been found that turn out to be in bijection with Littlewood–Richardson tableaux, and can therefore also be used to define the Littlewood–Richardson coefficients.
-(2,1)_word_112213.svg.png)
, 
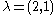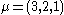and 
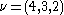. Then the fact that 
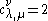can be deduced from the fact that the two tableaux shown at the right are the only two Littlewood–Richardson tableaux of shape 
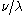and weight 
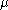. Indeed, since the last box on the first nonempty line of the skew diagram can only contain an entry 1, the entire first line must be filled with entries 1 (this is true for any Littlewood–Richardson tableau); in the last box of the second row we can only place a 2 by column strictness and the fact that our lattice word cannot contain any larger entry before it contains a 2. For the first box of the second row we can now either use a 1 or a 2. Once that entry is chosen, the third row must contain the remaining entries to make the weight (3,2,1), in a weakly increasing order, so we have no choice left any more; in both case it turns out that we do find a Littlewood–Richardson tableau.
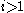occurs with index j, then that entry i[j] should occur in a row strictly below that of 
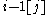(which certainly also occurs, since the entry i − 1 occurs as least as often as the entry i does). In fact the entry i[j] should also occur in a column no further to the right than that same entry 
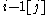(which at first sight appears to be a stricter condition). If the weight of the Littlewood–Richardson tableau is fixed beforehand, then one can form a fixed collection of indexed entries, and the if these are placed in a way respecting those geometric restrictions, in addition to those of semistandard tableaux and the condition that indexed copies of the same entries should respect right-to-left ordering of the indexes, then the resulting tableaux are guaranteed to be Littlewood–Richardson tableaux.
there is no simple criterion to determine whether any Littlewood–Richardson tableaux of shape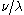 
and of weight 
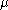exist at all (although there are a number of necessary conditions, the simplest of which is 
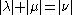); therefore it seems inevitable that in some cases one has to go through an elaborate search, only to find that no solutions exist.
Nevertheless, the rule leads to a quite efficient procedure to determine the full decomposition of a product of Schur functions, in other words to determine all coefficients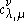
for fixed λ and μ, but varying ν. This fixes the weight of the Littlewood–Richardson tableaux to be constructed and the "inner part" λ of their shape, but leaves the "outer part" ν free. Since the weight is known, the set of indexed entries in the geometric description is fixed. Now for successive indexed entries, all possible positions allowed by the geometric restrictions can be tried in a backtracking
search. The entries can be tried in increasing order, while among equal entries they can be tried by decreasing index. The latter point is the key to efficiency of the search procedure: the entry i[j] is then restricted to be in a column to the right of
, but no further to the right than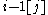 
(if such entries are present). This strongly restricts the set of possible positions, but always leaves at least one valid position for 
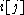; thus every placement of an entry will give rise to at least one complete Littlewood–Richardson tableau, and the search tree
contains no dead ends.
A similar method can be used to find all coefficients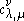
for fixed λ and ν, but varying μ.
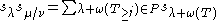
where the sum is over all tableaux T on μ/ν such that for all j, the sequence of integers λ+ω(T≥j) is non-increasing, and ω is the weight.
Pieri's formula
, which is the special case of the Littlewood–Richardson rule in the case when one of the partitions has only one part, states that
where Sn is the Schur function of a partition with one row and the sum is over all partitions λ obtained from μ by adding n elements to its Ferrers diagram, no two in the same column.
If both partitions are rectangular in shape, the sum is also multiplicity free . Fix a, b, p, and q positive integers with p
q. Denote by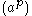 
the partition with p parts of length a. The partitions indexing nontrivial components of 
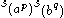are those partitions 
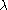with length 
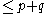such that
For example,
.
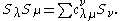
All coefficients with ν at most 4 are given by:
Most of the coefficients for small partitions are 0 or 1, which happens in particular whenever one of the factors is of the form Sn or S11...1, because of Pieri's formula
and its transposed counterpart. The simplest example with a coefficient larger than 1 happens when neither of the factors has this form:
For larger partitions the coefficients become more complicated. For example,
The original example given by was (after correcting for 3 tableaux they found but forgot to include in the final sum)
with 26 terms coming from the following 34 tableaux:
Calculating skew Schur functions is similar.
For example, the 15 Littlewood–Richardson tableaux for ν=5432 and λ=331 are
so S5432/331 = Σc Sμ = S52 + S511 + S4111 + S2221 + 2S43 + 2S3211 + 2S322 + 2S331 + 3S421 .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Littlewood–Richardson rule is a combinatorial description of the coefficients that arise when decomposing a product of two Schur functions
Schur polynomial
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
as a linear combination of other Schur functions. These coefficients are natural numbers, which the Littlewood–Richardson rule describes as counting certain skew tableaux. They occur in many other mathematical contexts, for instance as multiplicity in the decomposition of tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of irreducible representations of general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
s (or related groups like the special linear
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
and special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
s), or in the decomposition of certain induced representations in the representation theory of the symmetric group
Representation theory of the symmetric group
In mathematics, the representation theory of the symmetric group is a particular case of the representation theory of finite groups, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function theory to problems of quantum...
, or in the area of algebraic combinatorics
Algebraic combinatorics
Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra....
dealing with Young tableaux and symmetric polynomials
Littlewood–Richardson coefficients depend on three partitions, say
, of which and 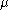describe the Schur functions being multiplied, and gives the Schur function of which this is the coefficient in the linear combination; in other words they are the coefficients 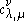such thatThe Littlewood–Richardson rule states that
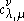is equal to the number of Littlewood–Richardson tableaux of shape 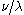and of weight 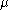.History
The Littlewood–Richardson rule was first stated by but though they claimed it as a theorem they only proved it in some fairly simple special cases.claimed to complete their proof, but his argument had gaps, though it was so obscurely written that these gaps were not noticed for some time, and his argument is reproduced in the book . Some of the gaps were later filled by . The first rigorous proofs of the rule were given four decades after it was found, by and , after the necessary combinatorial theory was developed by , , and in their work on the Robinson–Schensted correspondence.
There are now several short proofs of the rule, such as , and using Bender-Knuth involutions.
used the Littelmann path model
Littelmann path model
In mathematics, the Littelmann path model is a combinatorial device due to Peter Littelmann for computing multiplicities without overcounting in the representation theory of symmetrisable Kac-Moody algebras. Its most important application is to complex semisimple Lie algebras or equivalently...
to generalize the Littlewood–Richardson rule to other semisimple Lie groups.
The Littlewood–Richardson rule is notorious for the number of errors that appeared prior to its complete, published proof. Several published attempts to prove it are incomplete, and it is particularly difficult to avoid errors when doing hand calculations with it: even the original example in contains an error.
Littlewood–Richardson rule
The Littlewood–Richardson rule states that is equal to the number of Littlewood–Richardson tableaux of shape 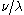and of weight 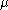.Littlewood–Richardson tableaux
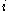occurs at least as often as the number . Another equivalent (though not quite obviously so) characterization is that the tableau itself, and any tableau obtained from it by removing some number of its leftmost columns, has a weakly decreasing weight. Many other combinatorial notions have been found that turn out to be in bijection with Littlewood–Richardson tableaux, and can therefore also be used to define the Littlewood–Richardson coefficients.Example
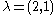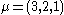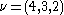Consider the case that, and . Then the fact that 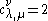can be deduced from the fact that the two tableaux shown at the right are the only two Littlewood–Richardson tableaux of shape 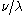and weight 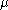. Indeed, since the last box on the first nonempty line of the skew diagram can only contain an entry 1, the entire first line must be filled with entries 1 (this is true for any Littlewood–Richardson tableau); in the last box of the second row we can only place a 2 by column strictness and the fact that our lattice word cannot contain any larger entry before it contains a 2. For the first box of the second row we can now either use a 1 or a 2. Once that entry is chosen, the third row must contain the remaining entries to make the weight (3,2,1), in a weakly increasing order, so we have no choice left any more; in both case it turns out that we do find a Littlewood–Richardson tableau.A more geometrical description
The condition that the sequence of entries read from the tableau in a somewhat peculiar order form a lattice word, can be replaced by a more local and geometrical condition. Since in a semistandard tableau equal entries never occur in the same column, one can number the copies of any value from right to left, which is their order in of occurrence in the sequence that should be a lattice word. Call the number so associated to each entry its index, and write an entry i with index j as i[j]. Now if some Littlewood–Richardson tableau contains an entry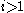 occurs with index j, then that entry i[j] should occur in a row strictly below that of 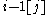(which certainly also occurs, since the entry i − 1 occurs as least as often as the entry i does). In fact the entry i[j] should also occur in a column no further to the right than that same entry 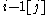(which at first sight appears to be a stricter condition). If the weight of the Littlewood–Richardson tableau is fixed beforehand, then one can form a fixed collection of indexed entries, and the if these are placed in a way respecting those geometric restrictions, in addition to those of semistandard tableaux and the condition that indexed copies of the same entries should respect right-to-left ordering of the indexes, then the resulting tableaux are guaranteed to be Littlewood–Richardson tableaux.An algorithmic form of the rule
The Littlewood–Richardson as stated above gives a combinatorial expression for individual Littlewood–Richardson coefficients, but gives no indication of a practical method to enumerate the Littlewood–Richardson tableaux in order to find the values of these coefficients. Indeed for given there is no simple criterion to determine whether any Littlewood–Richardson tableaux of shape 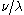and of weight 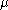exist at all (although there are a number of necessary conditions, the simplest of which is 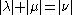); therefore it seems inevitable that in some cases one has to go through an elaborate search, only to find that no solutions exist.Nevertheless, the rule leads to a quite efficient procedure to determine the full decomposition of a product of Schur functions, in other words to determine all coefficients
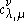for fixed λ and μ, but varying ν. This fixes the weight of the Littlewood–Richardson tableaux to be constructed and the "inner part" λ of their shape, but leaves the "outer part" ν free. Since the weight is known, the set of indexed entries in the geometric description is fixed. Now for successive indexed entries, all possible positions allowed by the geometric restrictions can be tried in a backtrackingBacktracking
Backtracking is a general algorithm for finding all solutions to some computational problem, that incrementally builds candidates to the solutions, and abandons each partial candidate c as soon as it determines that c cannot possibly be completed to a valid solution.The classic textbook example...
search. The entries can be tried in increasing order, while among equal entries they can be tried by decreasing index. The latter point is the key to efficiency of the search procedure: the entry i[j] is then restricted to be in a column to the right of
, but no further to the right than 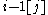(if such entries are present). This strongly restricts the set of possible positions, but always leaves at least one valid position for 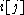; thus every placement of an entry will give rise to at least one complete Littlewood–Richardson tableau, and the search treeSearch tree
In computer science, a search tree is a binary tree data structure in whose nodes data values are stored from some ordered set, in such a way that in-order traversal of the tree visits the nodes in ascending order of the stored values...
contains no dead ends.
A similar method can be used to find all coefficients
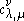for fixed λ and ν, but varying μ.Littlewood–Richardson coefficients
The Littlewood–Richardson coefficients c appear in the following ways:- They are the structure constants for the product in the ring of symmetric functions with respect to the basis of Schur functions
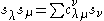
- or equivalently c is the inner product of sν and sλsμ.
- They express skew Schur functions in terms of Schur functions
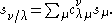
- The c appear as intersection numbers on a GrassmannianGrassmannianIn mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
:
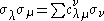
- They express skew Schur functions in terms of Schur functions
- where σμ is the class of the Schubert varietySchubert varietyIn algebraic geometry, a Schubert variety is a certain subvariety of a Grassmannian, usually with singular points. Described by means of linear algebra, a typical example consists of the k-dimensional subspaces V of an n dimensional vector space W, such that\dim\ge jfor j = 1, 2, ..., k,...
of a Grassmannian corresponding to μ.- c is the number of times the irreducible representation Vλ ⊗ Vμ of the product of symmetric groups S|λ| × S|μ| appears in the restriction of the representation Vν of S|ν| to S|λ| × S|μ|. By Frobenius reciprocity this is also the number of times that Vν occurs in the representation of S|ν| induced from Vλ ⊗ Vμ.
- The c appear in the decomposition of the tensor product of two Schur modules (irreducible representations of special linear groups)
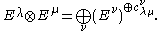
- c is the number of standard Young tableaux of shape ν/μ that are jeu de taquinJeu de taquinIn the mathematical field of combinatorics, jeu de taquin is a construction due to which defines an equivalence relation on the set of skew standard Young tableaux. A jeu de taquin slide is a transformation where the numbers in a tableau are moved around in a way similar to how the pieces in the...
equivalent to some fixed standard Young tableau of shape λ. - c is the number of Littlewood–Richardson tableaux of shape ν/λ and of weight μ.
- c is the number of picturesPicture (mathematics)In combinatorial mathematics, a picture is a bijection between skew diagrams satisfying certain properties, introduced by in a generalization of the Robinson–Schensted correspondence and the Littlewood–Richardson rule....
between μ and ν/λ.
Generalizations and special cases
extended the Littlewood–Richardson rule to skew Schur functions as follows: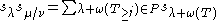where the sum is over all tableaux T on μ/ν such that for all j, the sequence of integers λ+ω(T≥j) is non-increasing, and ω is the weight.
Pieri's formula
Pieri's formula
In mathematics, Pieri's formula, named after Mario Pieri, describes the product of a Schubert cycle by a special Schubert cycle in the Schubert calculus, or the product of a Schur polynomial by a complete symmetric function....
, which is the special case of the Littlewood–Richardson rule in the case when one of the partitions has only one part, states that
where Sn is the Schur function of a partition with one row and the sum is over all partitions λ obtained from μ by adding n elements to its Ferrers diagram, no two in the same column.
If both partitions are rectangular in shape, the sum is also multiplicity free . Fix a, b, p, and q positive integers with p
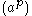q. Denote by the partition with p parts of length a. The partitions indexing nontrivial components of 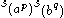are those partitions with length 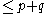such that
For example,
.
Examples
The examples of Littlewood-Richardson coefficients below are given in terms of products of Schur polynomials Sπ, indexed by partitions π, using the formula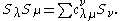All coefficients with ν at most 4 are given by:
- S0Sπ = Sπ for any π. where S0=1 is the Schur polynomial of the empty partition
- S1S1 = S2 + S11
- S2S1 = S3 + S21
- S11S1 = S111 + S21
- S3S1 = S4 + S31
- S21S1 = S31 + S22 + S211
- S2S2 = S4 + S31 + S22
- S2S11 = S31 + S211
- S111S1 = S1111 + S211
- S11S11 = S1111 + S211 + S22
Most of the coefficients for small partitions are 0 or 1, which happens in particular whenever one of the factors is of the form Sn or S11...1, because of Pieri's formula
Pieri's formula
In mathematics, Pieri's formula, named after Mario Pieri, describes the product of a Schubert cycle by a special Schubert cycle in the Schubert calculus, or the product of a Schur polynomial by a complete symmetric function....
and its transposed counterpart. The simplest example with a coefficient larger than 1 happens when neither of the factors has this form:
- S21S21 = S42 + S411 + S33 + 2S321 + S3111 + S222 + S2211.
For larger partitions the coefficients become more complicated. For example,
- S321S321 = S642 +S6411 +S633 +2S6321 +S63111 +S6222 +S62211 +S552 +S5511 +2S543 +4S5421 +2S54111 +3S5331 +3S5322 +4S53211 +S531111 +2S52221 +S522111 +S444 +3S4431 +2S4422 +3S44211 +S441111 +3S4332 +3S43311 +4S43221 +2S432111 +S42222 +S422211 +S3333 +2S33321 +S333111 +S33222 +S332211 with 34 terms and total multiplicity 62, and the largest coefficient is 4
- S4321S4321 is a sum of 206 terms with total multiplicity is 930, and the largest coefficient is 18.
- S54321S54321 is a sum of 1433 terms with total multiplicity 26704, and the largest coefficient (that of S86543211) is 176.
- S654321S654321 is a sum of 10873 terms with total multiplicity is 1458444 (so the average value of the coefficients is more than 100, and they can be as large as 2064).
The original example given by was (after correcting for 3 tableaux they found but forgot to include in the final sum)
- S431S221 = S652 + S6511 + S643 + 2S6421 + S64111 + S6331 + S6322 + S63211 + S553 + 2S5521 + S55111 + 2S5431 + 2S5422 + 3S54211 + S541111 + S5332 + S53311 + 2S53221 + S532111 + S4432 + S44311 + 2S44221 + S442111 + S43321 + S43222 + S432211
with 26 terms coming from the following 34 tableaux:
....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11
...22 ...22 ...2 ...2 ...2 ...2 ... ... ...
.3 . .23 .2 .3 . .22 .2 .2
3 3 2 2 3 23 2
3 3
....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1
...12 ...12 ...12 ...12 ...1 ...1 ...1 ...2 ...1
.23 .2 .3 . .23 .22 .2 .1 .2
3 2 2 2 3 23 23 2
3 3
....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1
...2 ...2 ...2 ... ... ... ... ...
.1 .3 . .12 .12 .1 .2 .2
2 1 1 23 2 22 13 1
3 2 2 3 3 2 2
3 3
.... .... .... .... .... .... .... ....
...1 ...1 ...1 ...1 ...1 ... ... ...
.12 .12 .1 .2 .2 .11 .1 .1
23 2 22 13 1 22 12 12
3 3 2 2 3 23 2
3 3
Calculating skew Schur functions is similar.
For example, the 15 Littlewood–Richardson tableaux for ν=5432 and λ=331 are
...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11
...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2
.11 .11 .11 .12 .11 .12 .13 .13 .23 .13 .13 .12 .12 .23 .23
12 13 22 12 23 13 12 24 14 14 22 23 33 13 34
so S5432/331 = Σc Sμ = S52 + S511 + S4111 + S2221 + 2S43 + 2S3211 + 2S322 + 2S331 + 3S421 .
External links
- An online program, decomposing products of Schur functions using the Littlewood–Richardson rule