
Drucker Prager yield criterion
Encyclopedia
The Drucker–Prager yield criterion has the form

where
 is the first invariant of the Cauchy stress
is the first invariant of the Cauchy stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
and
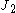 is the second invariant of the deviatoric part of the Cauchy stress
is the second invariant of the deviatoric part of the Cauchy stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
. The constants
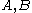 are determined from experiments.
are determined from experiments.In terms of the equivalent stress
Von Mises stress
The von Mises yield criterion suggests that the yielding of materials begins when the second deviatoric stress invariant J_2 reaches a critical value k. For this reason, it is sometimes called the J_2-plasticity or J_2 flow theory. It is part of a plasticity theory that applies best to ductile...
(or von Mises stress
Von Mises stress
The von Mises yield criterion suggests that the yielding of materials begins when the second deviatoric stress invariant J_2 reaches a critical value k. For this reason, it is sometimes called the J_2-plasticity or J_2 flow theory. It is part of a plasticity theory that applies best to ductile...
) and the hydrostatic (or mean) stress
Hydrostatic stress
In continuum mechanics, a hydrostatic stress is an isotropic stress that is given by the weight of water above a certain point. It is often used interchangeably with "pressure" and is also known as confining stress, particularly in the field geomechanics...
, the Drucker–Prager criterion can be expressed as
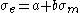
where
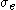 is the equivalent stress,
is the equivalent stress, 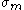 is the hydrostatic stress, and
is the hydrostatic stress, and are material constants. The Drucker–Prager yield criterion expressed in Haigh–Westergaard coordinates is
are material constants. The Drucker–Prager yield criterion expressed in Haigh–Westergaard coordinates is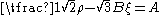
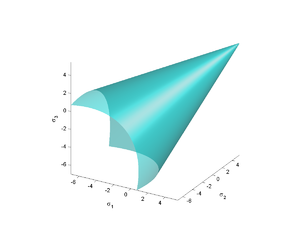
The Drucker–Prager yield surface is a smooth version of the Mohr–Coulomb yield surface.
Expressions for A and B
The Drucker–Prager model can be written in terms of the principal stresses as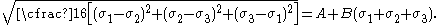
If
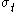 is the yield stress in uniaxial tension, the Drucker–Prager criterion implies
is the yield stress in uniaxial tension, the Drucker–Prager criterion implies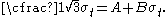
If
 is the yield stress in uniaxial compression, the Drucker–Prager criterion implies
is the yield stress in uniaxial compression, the Drucker–Prager criterion implies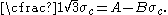
Solving these two equations gives
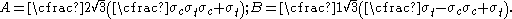
Uniaxial asymmetry ratio
Different uniaxial yield stresses in tension and in compression are predicted by the Drucker–Prager model. The uniaxial asymmetry ratio for the Drucker–Prager model is
Expressions in terms of cohesion and friction angle
Since the Drucker–Prager yield surfaceYield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
is a smooth version of the Mohr–Coulomb yield surface
Mohr-Coulomb theory
Mohr–Coulomb theory is a mathematical model describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope...
, it is often expressed in terms of the cohesion (
 ) and the angle of internal friction (
) and the angle of internal friction (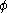 ) that are used to describe the Mohr–Coulomb yield surface
) that are used to describe the Mohr–Coulomb yield surfaceMohr-Coulomb theory
Mohr–Coulomb theory is a mathematical model describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope...
. If we assume that the Drucker–Prager yield surface circumscribes the Mohr–Coulomb yield surface then the expressions for
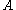 and
and 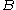 are
are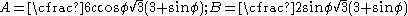
If the Drucker–Prager yield surface inscribes the Mohr–Coulomb yield surface then
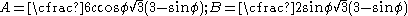
Derivation of expressions for 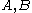 in terms of in terms of 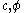 |
|---|
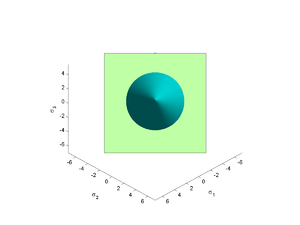
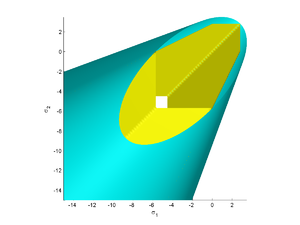
| The expression for the Mohr–Coulomb yield criterion Mohr-Coulomb theory Mohr–Coulomb theory is a mathematical model describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope... in Haigh–Westergaard space is 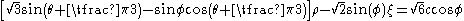 If we assume that the Drucker–Prager yield surface circumscribes the Mohr–Coulomb yield surface such that the two surfaces coincide at 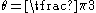 , then at those points the Mohr–Coulomb yield surface can be expressed as , then at those points the Mohr–Coulomb yield surface can be expressed as or,  The Drucker–Prager yield criterion expressed in Haigh–Westergaard coordinates is 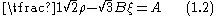 Comparing equations (1.1) and (1.2), we have  These are the expressions for  in terms of in terms of 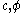 . .On the other hand if the Drucker–Prager surface inscribes the Mohr–Coulomb surface, then matching the two surfaces at 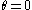 gives gives  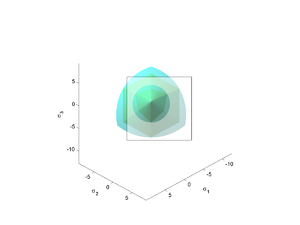 |
 |
 |
||
Drucker–Prager model for polymers
The Drucker–Prager model has been used to model polymers such as polyoxymethylenePolyoxymethylene
Polyoxymethylene , also known as acetal, polyacetal, and polyformaldehyde, is an engineering thermoplastic used in precision parts that require high stiffness, low friction and excellent dimensional stability....
and polypropylene
Polypropylene
Polypropylene , also known as polypropene, is a thermoplastic polymer used in a wide variety of applications including packaging, textiles , stationery, plastic parts and reusable containers of various types, laboratory equipment, loudspeakers, automotive components, and polymer banknotes...
. For polyoxymethylene
Polyoxymethylene
Polyoxymethylene , also known as acetal, polyacetal, and polyformaldehyde, is an engineering thermoplastic used in precision parts that require high stiffness, low friction and excellent dimensional stability....
the yield stress is a linear function of the pressure. However, polypropylene
Polypropylene
Polypropylene , also known as polypropene, is a thermoplastic polymer used in a wide variety of applications including packaging, textiles , stationery, plastic parts and reusable containers of various types, laboratory equipment, loudspeakers, automotive components, and polymer banknotes...
shows a quadratic pressure-dependence of the yield stress.
Drucker–Prager model for foams
For foams, the GAZT model uses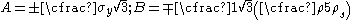
where
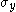 is a critical stress for failure in tension or compression,
is a critical stress for failure in tension or compression,  is the density of the foam, and
is the density of the foam, and 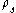 is the density of the base material.
is the density of the base material.Extensions of the isotropic Drucker–Prager model
The Drucker–Prager criterion can also be expressed in the alternative form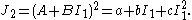
Deshpande–Fleck yield criterion
The Deshpande–Fleck yield criterion for foams has the form given in above equation. The parameters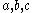 for the Deshpande–Fleck criterion are
for the Deshpande–Fleck criterion are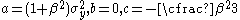
where
 is a parameter that determines the shape of the yield surface, and
is a parameter that determines the shape of the yield surface, and  is the yield stress in tension or compression.
is the yield stress in tension or compression.Anisotropic Drucker–Prager yield criterion
An anisotropic form of the Drucker–Prager yield criterion is the Liu–Huang–Stout yield criterion . This yield criterion is an extension of the generalized Hill yield criterionHill yield criteria
Rodney Hill has developed several yield criteria for anisotropic plastic deformations. The earliest version was a straightforward extension of the von Mises yield criterion and had a quadratic form. This model was later generalized by allowing for an exponent m...
and has the form
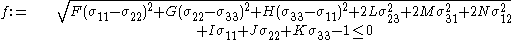
The coefficients
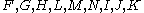 are
are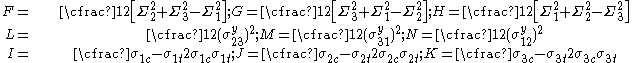
where
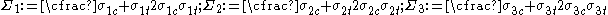
and
 are the uniaxial yield stresses in compression in the three principal directions of anisotropy,
are the uniaxial yield stresses in compression in the three principal directions of anisotropy,  are the uniaxial yield stresses in tension, and
are the uniaxial yield stresses in tension, and 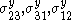 are the yield stresses in pure shear.
are the yield stresses in pure shear.The Drucker yield criterion
The Drucker–Prager criterion should not be confused with the earlier Drucker criterion which is independent of the pressure (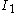 ). The Drucker yield criterion has the form
). The Drucker yield criterion has the form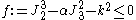
where
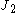 is the second invariant of the deviatoric stress,
is the second invariant of the deviatoric stress, 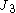 is the third invariant of the deviatoric stress,
is the third invariant of the deviatoric stress,  is a constant that lies between -27/8 and 9/4 (for the yield surface to be convex),
is a constant that lies between -27/8 and 9/4 (for the yield surface to be convex), 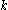 is a constant that varies with the value of
is a constant that varies with the value of  . For
. For 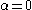 ,
,  where
where 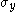 is the yield stress in uniaxial tension.
is the yield stress in uniaxial tension.Anisotropic Drucker Criterion
An anisotropic version of the Drucker yield criterion is the Cazacu–Barlat (CZ) yield criterion which has the form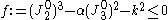
where
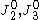 are generalized forms of the deviatoric stress and are defined as
are generalized forms of the deviatoric stress and are defined as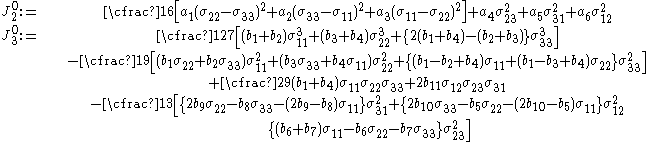
Cazacu–Barlat yield criterion for plane stress
For thin sheet metals, the state of stress can be approximated as plane stress. In that case the Cazacu–Barlat yield criterion reduces to its two-dimensional version with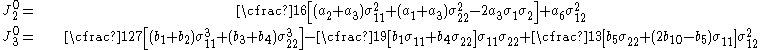
For thin sheets of metals and alloys, the parameters of the Cazacu–Barlat yield criterion are
| Material | 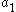 | 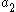 |  |  |  |  | 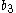 | 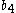 |  | 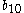 |  |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 6016-T4 Aluminum Alloy | 0.815 | 0.815 | 0.334 | 0.42 | 0.04 | -1.205 | -0.958 | 0.306 | 0.153 | -0.02 | 1.4 |
| 2090-T3 Aluminum Alloy | 1.05 | 0.823 | 0.586 | 0.96 | 1.44 | 0.061 | -1.302 | -0.281 | -0.375 | 0.445 | 1.285 |
See also
- Yield surfaceYield surfaceA yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
- Yield (engineering)Yield (engineering)The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
- Plasticity (physics)Plasticity (physics)In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
- Failure theory (material)Failure theory (material)Failure theory is the science of predicting the conditions under which solid materials fail under the action of external loads. The failure of a material is usually classified into brittle failure or ductile failure . Depending on the conditions most materials can fail in a brittle or ductile...

