
Well-defined
Encyclopedia
In mathematics
, well-definition is a mathematical or logical definition of a certain concept or object (a function
, a property
, a relation
, etc.) which uses a set of base axiom
s in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy the required properties. Sometimes however, it is economical to state a definition in terms of an arbitrary choice; one then has to check that the definition is independent of that choice. On other occasions, the required properties might not all be obvious; one then has to verify them. These issues commonly arise in the definition of functions.
For instance, in group theory
, the term well-defined is often used when dealing with coset
s, where a function on a coset space is often defined by choosing a representative: it is then just as important that we get the same result regardless of which representative of the coset we choose.
As an example, take the definition:
f(x1)=f(x2) if x1~x2
then the definition makes sense, and f is well-defined on X/~. Although the distinction is often ignored, the function on X/~, having a different domain, should be viewed as a distinct map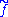 .
.
As an example, consider the equivalence relation between real numbers defined by θ1~θ2 if there is an integer n such that θ1-θ2 = 2πn, where π (not italicized) denotes Pi
. The quotient set X/~ may then be identified with a circle, as an equivalence class [θ] represents an angle. (In fact this is the coset space R/2πZ of the additive subgroup 2πZ of R.) Now if f:R→R is the cosine function, then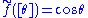 is well-defined, whereas if f(θ) = θ then
is well-defined, whereas if f(θ) = θ then 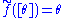 is not well-defined function; in other words, it is a multivalued function
is not well-defined function; in other words, it is a multivalued function
.
Two other issues of well-definition arise when defining a function f from a set X to a set Y. First, f should actually be defined on all elements of X. For example, the function f(x) = 1/x is not well-defined as a function from the real numbers to itself, as f(0) is not defined. Secondly, f(x) should be an element of Y for all x∈X. For example, the function f(x) = x2 is not well-defined as a function from the real numbers to the positive real numbers, as f(0) is not positive.
A set is well-defined if any given object either is an element of the set, or is not an element
of the set.
, if f is a partial function
on S and a is an element of S, then this is written as f(a)↓ and is read "f(a) is defined."
If a is not in the domain of f, then f(a)↑ is written and is read as "f(a) is undefined".
One very common case of what "sensible" can mean is in the context of continuous function
s. For instance, the real-valued function f(x) = (2x)/x is undefined for x = 0 (because the denominator becomes zero), but it can be extended continuously by defining f(x) = 2 for all real x.
On the other hand, the function q(x,y) = x/y is defined for any real number
x and any real number y different from 0. It is undefined for y=0 and cannot be extended continuously to any point (x,0). This is expressed in short by: you cannot divide by zero
.
, measure theory, and other mathematical disciplines, the symbol ∞
is frequently used to denote an infinite pseudo-number, in real analysis alongside with its negative -∞. The symbol has no well-defined meaning by itself, but an expression like an → ∞ is a shorthand for a divergent sequence which is eventually larger than any given real number.
Arithmetic with the symbols ±∞ is undefined. The following conventions of addition and multiplication are in common use:
No sensible extension of addition and multiplication with ∞ exist in the following cases:
, ab, is defined for all natural numbers b as an iterated product. If a ≠ 0, one defines a-b as 1/ab for b>0 and a0 = 1. The expression 0b is undefined for b ≤ 0, although a common convention is to define 00 as 1.
For rational exponents b=p/q and real positive basis a, the power ab is defined as the qth root
of ap; this can be extended continuously to all real exponents b. If a < 0, there is no sensible definition of the power.
, a point x where a holomorphic function
is undefined is called a singularity
. One distinguishes between removable singularities (the function can be extended holomorphically to x, poles (the function can be extended meromorphically
to x), and essential singularities
, where no meromorphic extension to x exists.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, well-definition is a mathematical or logical definition of a certain concept or object (a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, a property
Property (philosophy)
In modern philosophy, logic, and mathematics a property is an attribute of an object; a red object is said to have the property of redness. The property may be considered a form of object in its own right, able to possess other properties. A property however differs from individual objects in that...
, a relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
, etc.) which uses a set of base axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy the required properties. Sometimes however, it is economical to state a definition in terms of an arbitrary choice; one then has to check that the definition is independent of that choice. On other occasions, the required properties might not all be obvious; one then has to verify them. These issues commonly arise in the definition of functions.
For instance, in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the term well-defined is often used when dealing with coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s, where a function on a coset space is often defined by choosing a representative: it is then just as important that we get the same result regardless of which representative of the coset we choose.
As an example, take the definition:
f(x1)=f(x2) if x1~x2
then the definition makes sense, and f is well-defined on X/~. Although the distinction is often ignored, the function on X/~, having a different domain, should be viewed as a distinct map
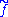 .
.As an example, consider the equivalence relation between real numbers defined by θ1~θ2 if there is an integer n such that θ1-θ2 = 2πn, where π (not italicized) denotes Pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
. The quotient set X/~ may then be identified with a circle, as an equivalence class [θ] represents an angle. (In fact this is the coset space R/2πZ of the additive subgroup 2πZ of R.) Now if f:R→R is the cosine function, then
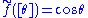 is well-defined, whereas if f(θ) = θ then
is well-defined, whereas if f(θ) = θ then 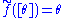 is not well-defined function; in other words, it is a multivalued function
is not well-defined function; in other words, it is a multivalued functionMultivalued function
In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
.
Two other issues of well-definition arise when defining a function f from a set X to a set Y. First, f should actually be defined on all elements of X. For example, the function f(x) = 1/x is not well-defined as a function from the real numbers to itself, as f(0) is not defined. Secondly, f(x) should be an element of Y for all x∈X. For example, the function f(x) = x2 is not well-defined as a function from the real numbers to the positive real numbers, as f(0) is not positive.
A set is well-defined if any given object either is an element of the set, or is not an element
of the set.
Notation using ↓ and ↑
In computability theoryComputability theory (computer science)
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science...
, if f is a partial function
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
on S and a is an element of S, then this is written as f(a)↓ and is read "f(a) is defined."
If a is not in the domain of f, then f(a)↑ is written and is read as "f(a) is undefined".
Undefined values
In common mathematical usage, an arithmetic expressionE(x,y,...) is called undefined for certain values x0, y0,... of the variables x, y, ... in two different cases:- A meaning for E(x0,y0,...) has not been specified in the definition of E.
- The same, and in addition there is no "sensible" way to extend the existing definition to cover the case x0,...
One very common case of what "sensible" can mean is in the context of continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s. For instance, the real-valued function f(x) = (2x)/x is undefined for x = 0 (because the denominator becomes zero), but it can be extended continuously by defining f(x) = 2 for all real x.
On the other hand, the function q(x,y) = x/y is defined for any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
x and any real number y different from 0. It is undefined for y=0 and cannot be extended continuously to any point (x,0). This is expressed in short by: you cannot divide by zero
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
.
The symbols of infinity
In analysisAnalysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
, measure theory, and other mathematical disciplines, the symbol ∞
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
is frequently used to denote an infinite pseudo-number, in real analysis alongside with its negative -∞. The symbol has no well-defined meaning by itself, but an expression like an → ∞ is a shorthand for a divergent sequence which is eventually larger than any given real number.
Arithmetic with the symbols ±∞ is undefined. The following conventions of addition and multiplication are in common use:
- ∞ + x = ∞ for all reals x and x = ∞, -∞ + x = -∞ for all reals x and x = -∞
- x ∞ = ∞ for positive reals x>0.
No sensible extension of addition and multiplication with ∞ exist in the following cases:
- ∞ - ∞
- 0 ∞ (although in measure theory, this is often defined as 0)
- ∞/∞
Undefined forms of exponentiation
The operation of exponentiationExponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
, ab, is defined for all natural numbers b as an iterated product. If a ≠ 0, one defines a-b as 1/ab for b>0 and a0 = 1. The expression 0b is undefined for b ≤ 0, although a common convention is to define 00 as 1.
For rational exponents b=p/q and real positive basis a, the power ab is defined as the qth root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
of ap; this can be extended continuously to all real exponents b. If a < 0, there is no sensible definition of the power.
Singularities in complex analysis
In complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a point x where a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
is undefined is called a singularity
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
. One distinguishes between removable singularities (the function can be extended holomorphically to x, poles (the function can be extended meromorphically
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
to x), and essential singularities
Essential singularity
In complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
, where no meromorphic extension to x exists.
See also
- ExistenceExistenceIn common usage, existence is the world we are aware of through our senses, and that persists independently without them. In academic philosophy the word has a more specialized meaning, being contrasted with essence, which specifies different forms of existence as well as different identity...
- Uniqueness
- DefinitionismDefinitionismDefinitionism is the school of thought in which it is believed that a proper explanation of a theory consists of all the concepts used by that theory being well-defined. This approach has been criticized for its dismissal of the importance of ostensive definitions....
- Uniqueness quantificationUniqueness quantificationIn mathematics and logic, the phrase "there is one and only one" is used to indicate that exactly one object with a certain property exists. In mathematical logic, this sort of quantification is known as uniqueness quantification or unique existential quantification.Uniqueness quantification is...

