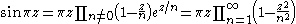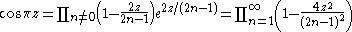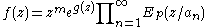Weierstrass factorization theorem
Encyclopedia
In mathematics
, the Weierstrass factorization theorem in complex analysis
, named after Karl Weierstrass
, asserts that entire function
s can be represented by a product involving their zeroes
. In addition, every sequence tending to infinity has an associated entire function with zeroes at precisely the points of that sequence.
A second form extended to meromorphic function
s allows one to consider a given meromorphic function as a product of three factors: the function's poles, zeroes, and an associated non-zero holomorphic function.
are twofold.
Firstly, any finite sequence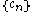
in the complex plane
has an associated polynomial
that has zeroes precisely at the points of that sequence
,
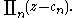
Secondly, any polynomial function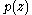
in the complex plane has a factorization
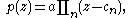
where a is a non-zero constant and cn are the zeroes of p.
The two forms of the Weierstrass factorization theorem can be thought of as extensions of the above to entire functions. The necessity of extra machinery is demonstrated when one considers the product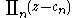
if the sequence 
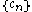is not finite. It can never define an entire function, because the infinite product does not converge. Thus one cannot, in general, define an entire function from a sequence of prescribed zeroes or represent an entire function by its zeroes using the expressions yielded by the fundamental theorem of algebra.
A necessary condition for convergence of the infinite product in question is that each factor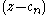
must approach 1 as 
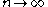. So it stands to reason that one should seek a function that could be 0 at a prescribed point, yet remain near 1 when not at that point and furthermore introduce no more zeroes than those prescribed. Enter the genius of Weierstrass' elementary factors. These factors serve the same purpose as the factors 
above.
For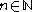
, define the elementary factors:
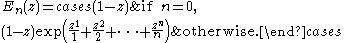
Their utility lies in the following lemma:
Lemma (15.8, Rudin) for |z| ≤ 1, n ∈ No
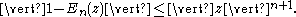
Let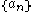
be a sequence of non-zero complex numbers such that 
.
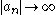If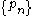
is any sequence of integers such that for all 
,
then the function
is entire with zeros only at points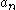
. If number 
occurs in sequence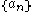 
exactly m times, then function f has a zero at 
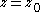of multiplicity m.
Let ƒ be an entire function, and let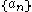
be the non-zero zeros of ƒ repeated according to multiplicity; suppose also that ƒ has a zero at z = 0 of order m ≥ 0 (a zero of order m = 0 at z = 0 means ƒ(0) ≠ 0).
Then there exists an entire function g and a sequence of integers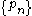
such that
ρ then it admits a factorization
where g(z) is a polynomial of degree q, and q ≤ ρ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Weierstrass factorization theorem in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, named after Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
, asserts that entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
s can be represented by a product involving their zeroes
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
. In addition, every sequence tending to infinity has an associated entire function with zeroes at precisely the points of that sequence.
A second form extended to meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s allows one to consider a given meromorphic function as a product of three factors: the function's poles, zeroes, and an associated non-zero holomorphic function.
Motivation
The consequences of the fundamental theorem of algebraFundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
are twofold.
Firstly, any finite sequence
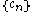in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
has an associated polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
that has zeroes precisely at the points of that sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
,
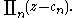
Secondly, any polynomial function
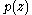in the complex plane has a factorizationFactorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
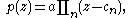
where a is a non-zero constant and cn are the zeroes of p.
The two forms of the Weierstrass factorization theorem can be thought of as extensions of the above to entire functions. The necessity of extra machinery is demonstrated when one considers the product
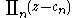if the sequence 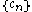is not finite. It can never define an entire function, because the infinite product does not converge. Thus one cannot, in general, define an entire function from a sequence of prescribed zeroes or represent an entire function by its zeroes using the expressions yielded by the fundamental theorem of algebra.A necessary condition for convergence of the infinite product in question is that each factor
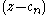must approach 1 as 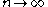. So it stands to reason that one should seek a function that could be 0 at a prescribed point, yet remain near 1 when not at that point and furthermore introduce no more zeroes than those prescribed. Enter the genius of Weierstrass' elementary factors. These factors serve the same purpose as the factors above.The elementary factors
These are also referred to as primary factors.For
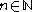, define the elementary factors: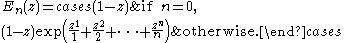Their utility lies in the following lemma:
Lemma (15.8, Rudin) for |z| ≤ 1, n ∈ No
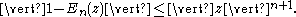
Existence of entire function with specified zeroes
Sometimes called the Weierstrass theorem.Let
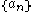be a sequence of non-zero complex numbers such that 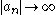.If
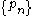is any sequence of integers such that for all ,
then the function
is entire with zeros only at points
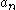. If number occurs in sequence 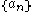exactly m times, then function f has a zero at 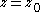of multiplicity m.- Note that the sequence
in the statement of the theorem always exists. For example we could always take 
and have the convergence. Such a sequence is not unique: changing it at finite number of positions, or taking another sequence p'n ≥ pn, will not break the convergence. - The theorem generalizes to the following: sequencesSéquencesSéquences is a French-language film magazine originally published in Montreal, Quebec by the Commission des ciné-clubs du Centre catholique du cinéma de Montréal, a Roman Catholic film society. Founded in 1955, the publication was edited for forty years by Léo Bonneville, a member of the Clerics...
in open subsets (and hence regions) of the Riemann sphereRiemann sphereIn mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
have associated functions that are holomorphic in those subsets and have zeroes at the points of the sequence. - Note also that the case given by the fundamental theorem of algebra is incorporated here. If the sequence
is finite then we can take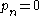 
and obtain: 
.
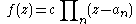The Weierstrass factorization theorem
Sometimes called the Weierstrass product/factor theorem.Let ƒ be an entire function, and let
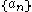be the non-zero zeros of ƒ repeated according to multiplicity; suppose also that ƒ has a zero at z = 0 of order m ≥ 0 (a zero of order m = 0 at z = 0 means ƒ(0) ≠ 0).Then there exists an entire function g and a sequence of integers
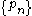such that
Examples of factorization
Hadamard factorization theorem
If ƒ is an entire function of finite orderEntire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
ρ then it admits a factorization
where g(z) is a polynomial of degree q, and q ≤ ρ.