
Elliptic cylindrical coordinates
Encyclopedia
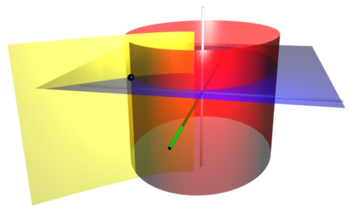
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
that results from projecting the two-dimensional elliptic coordinate system
Elliptic coordinates
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in whichthe coordinate lines are confocal ellipses and hyperbolae...
in the
perpendicular
 -direction. Hence, the coordinate surfaces are prisms
-direction. Hence, the coordinate surfaces are prismsPrism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
of confocal ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s and hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
e. The two foci
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
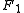 and
and 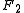 are generally taken to be fixed at
are generally taken to be fixed at 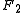 and
and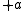 , respectively, on the
, respectively, on the  -axis of the Cartesian coordinate system
-axis of the Cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
.
Basic definition
The most common definition of elliptic cylindrical coordinates is
is
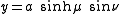

where
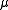 is a nonnegative real number and
is a nonnegative real number and 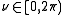 .
.These definitions correspond to ellipses and hyperbolae. The trigonometric identity
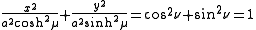
shows that curves of constant
 form ellipse
form ellipseEllipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s, whereas the hyperbolic trigonometric identity
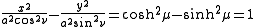
shows that curves of constant
 form hyperbola
form hyperbolaHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
e.
Scale factors
The scale factors for the elliptic cylindrical coordinates and
and  are equal
are equal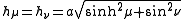
whereas the remaining scale factor
 .
.Consequently, an infinitesimal volume element equals

and the Laplacian equals
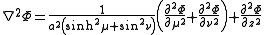
Other differential operators such as
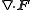 and
and 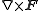 can be expressed in the coordinates
can be expressed in the coordinates 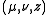 by substituting
by substitutingthe scale factors into the general formulae found in orthogonal coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
Alternative definition
An alternative and geometrically intuitive set of elliptic coordinates are sometimes used, where
are sometimes used, where  and
and 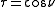 . Hence, the curves of constant
. Hence, the curves of constant  are ellipses, whereas the curves of constant
are ellipses, whereas the curves of constant  are hyperbolae. The coordinate
are hyperbolae. The coordinate  must belong to the interval [-1, 1], whereas the
must belong to the interval [-1, 1], whereas the 
coordinate must be greater than or equal to one.
The coordinates
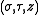 have a simple relation to the distances to the foci
have a simple relation to the distances to the foci 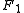 and
and 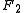 . For any point in the (x,y) plane, the sum
. For any point in the (x,y) plane, the sum 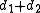 of its distances to the foci equals
of its distances to the foci equals  , whereas their difference
, whereas their difference 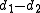 equals
equals 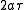 .
.Thus, the distance to
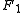 is
is 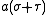 , whereas the distance to
, whereas the distance to  is
is 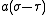 . (Recall that
. (Recall that 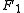 and
and 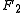 are located at
are located at 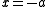 and
and  , respectively.)
, respectively.)A drawback of these coordinates is that they do not have a 1-to-1 transformation to the Cartesian coordinates
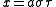
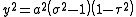
Alternative scale factors
The scale factors for the alternative elliptic coordinates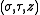 are
are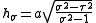

and, of course,
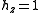 . Hence, the infinitesimal volume element becomes
. Hence, the infinitesimal volume element becomes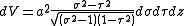
and the Laplacian equals
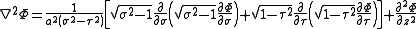
Other differential operators such as
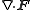
and
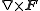 can be expressed in the coordinates
can be expressed in the coordinates 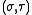 by substituting
by substitutingthe scale factors into the general formulae
found in orthogonal coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
Applications
The classic applications of elliptic cylindrical coordinates are in solving partial differential equations,e.g., Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
or the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
, for which elliptic cylindrical coordinates allow a
separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
. A typical example would be the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
surrounding a
flat conducting plate of width
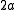 .
.The three-dimensional wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, when expressed in elliptic cylindrical coordinates, may be solved by separation of variables, leading to the Mathieu differential equations.
The geometric properties of elliptic coordinates can also be useful. A typical example might involve
an integration over all pairs of vectors
 and
and 
that sum to a fixed vector
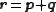 , where the integrand
, where the integrandwas a function of the vector lengths
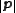 and
and 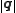 . (In such a case, one would position
. (In such a case, one would position  between the two foci and aligned with the
between the two foci and aligned with the  -axis, i.e.,
-axis, i.e., 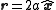 .) For concreteness,
.) For concreteness,  ,
, 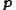 and
and 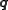 could represent the momenta
could represent the momentaMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
of a particle and its decomposition products, respectively, and the integrand might involve the kinetic energies of the products (which are proportional to the squared lengths of the momenta).

