Localized time-varying charge and current densities can act as sources of electromagnetic waves in a vacuum. Maxwell's equations

Maxwell's equations

Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...

 can be written in the form of a inhomogeneous electromagnetic wave equation

Electromagnetic wave equation

The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...

(or often "nonhomogeneous electromagnetic wave equation") with sources. The addition of sources to the wave equations makes the partial differential equations inhomogeneous.
Maxwell's equations in a vacuum with charge 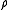and current 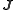sources can be written in terms of the vector and scalar potentials as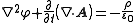



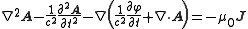
where


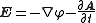
and
.

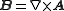If the Lorenz gauge condition

Lorenz gauge condition

In electromagnetism, the Lorenz gauge or Lorenz gauge condition is a partial gauge fixing of the electromagnetic vector potential. The condition is that \partial_\mu A^\mu=0...

 is assumed


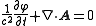
then the nonhomogeneous wave equations become

.
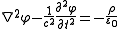
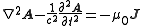In cgs units these equations become



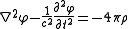
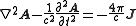
with



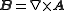
and the Lorenz gauge condition
.

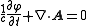For Lorentz–Heaviside units, sometimes used in high dimensional relativistic calculations, the charge and current densities in cgs units translate as

.
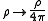
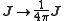The relativistic Maxwell's equations

Formulation of Maxwell's equations in special relativity

The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form which is "manifestly covariant" , in the formalism of special relativity...

 can be written in covariant

Covariance and contravariance

In multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis from one coordinate system to another. When one coordinate system is just a rotation of the other, this...

 form as


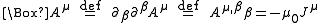
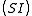
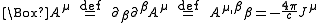
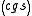
where J is the four-current

Four-current

In special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...

,


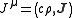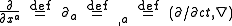
is the 4-gradient

Four-gradient

The four-gradient is the four-vector generalization of the gradient:\partial_\alpha \ = \left...

 and the electromagnetic four-potential

Electromagnetic four-potential

The electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...

 is


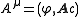
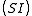
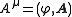
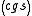
with the Lorenz gauge condition
.

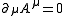Here
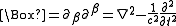is the d'Alembert operator

D'Alembert operator

In special relativity, electromagnetism and wave theory, the d'Alembert operator , also called the d'Alembertian or the wave operator, is the Laplace operator of Minkowski space. The operator is named for French mathematician and physicist Jean le Rond d'Alembert...

.
The electromagnetic wave equation is modified in two ways in curved spacetime, the derivative is replaced with the covariant derivative

Covariant derivative

In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...

 and a new term that depends on the curvature appears (SI units).


where


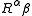
is the Ricci curvature tensor.