
Numerical ordinary differential equations
Encyclopedia
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
which studies the numerical solution of ordinary differential equations
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
(ODEs). This field is also known under the name numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
, but some people reserve this term for the computation of integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s.
Many differential equations cannot be solved analytically; however, in science and engineering, a numeric approximation to the solution is often good enough to solve a problem. The algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s studied here can be used to compute such an approximation. An alternative method is to use techniques from calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
to obtain a series expansion
Series expansion
In mathematics, a series expansion is a method for calculating a function that cannot be expressed by just elementary operators . The resulting so-called series often can be limited to a finite number of terms, thus yielding an approximation of the function...
of the solution.
Ordinary differential equations occur in many scientific disciplines, for instance in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, and economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
. In addition, some methods in numerical partial differential equations
Numerical partial differential equations
Numerical partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations .Numerical techniques for solving PDEs include the following:...
convert the partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
into an ordinary differential equation, which must then be solved.
The problem
We want to approximate the solution of the differential equation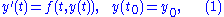
where f is a function that maps [t0,∞) × Rd to Rd, and the initial condition y0 ∈ Rd is a given vector.
The above formulation is called an initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
(IVP). The Picard–Lindelöf theorem states that there is a unique solution, if f is Lipschitz continuous. In contrast, boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s (BVPs) specify (components of) the solution y at more than one point. Different methods need to be used to solve BVPs, for example the shooting method
Shooting method
In numerical analysis, the shooting method is a method for solving a boundary value problem by reducing it to the solution of an initial value problem...
(and its variants) or global methods like finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
s, Galerkin method
Galerkin method
In mathematics, in the area of numerical analysis, Galerkin methods are a class of methods for converting a continuous operator problem to a discrete problem. In principle, it is the equivalent of applying the method of variation of parameters to a function space, by converting the equation to a...
s, or collocation method
Collocation method
In mathematics, a collocation method is a method for the numerical solution of ordinary differential equations, partial differential equations and integral equations...
s.
Note that we restrict ourselves to first-order differential equations (meaning that only the first derivative of y appears in the equation, and no higher derivatives). However, a higher-order equation can easily be converted to a system of first-order equations by introducing extra variables. For example, the second-order equation y
Methods
Three elementary methods are discussed to give the reader a feeling for the subject. After that, pointers are provided to other methods (which are generally more accurate and efficient). The methods mentioned here are analysed in the next section.The Euler method
A brief explanation:From any point on a curve, you can find an approximation of a nearby point on the curve by moving a short distance along a line tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the curve.
Rigorous development:
Starting with the differential equation (1), we replace the derivative y
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
approximation
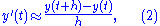
which when re-arranged yields the following formula
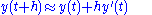
and using (1) gives:
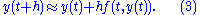
This formula is usually applied in the following way. We choose a step size h, and we construct the sequence t0, t1 = t0 + h, t2 = t0 + 2h, … We denote by yn a numerical estimate of the exact solution y(tn). Motivated by (3), we compute these estimates by the following recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
scheme
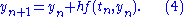
This is the Euler method (or forward Euler method, in contrast with the backward Euler method, to be described below). The method is named after Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
who described it in 1768.
The Euler method is an example of an explicit
Explicit and implicit methods
Explicit and implicit methods are approaches used in numerical analysis for obtaining numerical solutions of time-dependent ordinary and partial differential equations, as is required in computer simulations of physical processes....
method. This means that the new value yn+1 is defined in terms of things that are already known, like yn.
The backward Euler method
If, instead of (2), we use the approximation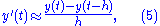
we get the backward Euler method:
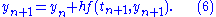
The backward Euler method is an implicit
Explicit and implicit methods
Explicit and implicit methods are approaches used in numerical analysis for obtaining numerical solutions of time-dependent ordinary and partial differential equations, as is required in computer simulations of physical processes....
method, meaning that we have to solve an equation to find yn+1. One often uses fixed point iteration or (some modification of) the Newton–Raphson method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
to achieve this. Of course, it costs time to solve this equation; this cost must be taken into consideration when one selects the method to use. The advantage of implicit methods such as (6) is that they are usually more stable for solving a stiff equation
Stiff equation
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
, meaning that a larger step size h can be used.
The exponential Euler method
If the differential equation is of the form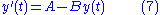
then an approximate explicit solution can be given by
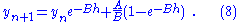
This method is commonly employed in neural simulations and it is the default integrator in the GENESIS
GENESIS (software)
GENESIS is a simulation environment for constructing realistic models of neurobiological systems at many levels of scale including subcellular processes, individual neurons, networks of neurons, and neuronal systems.GENESIS was developed in the Caltech laboratory of Dr. James M...
neural simulator.
Generalizations
The Euler method is often not accurate enough. In more precise terms, it only has order one (the concept of order is explained below). This caused mathematicians to look for higher-order methods.One possibility is to use not only the previously computed value yn to determine yn+1, but to make the solution depend on more past values. This yields a so-called multistep method. Perhaps the simplest is the Leapfrog method which is second order and (roughly speaking) relies on two time values.
Almost all practical multistep methods fall within the family of linear multistep methods, which have the form
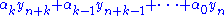
-
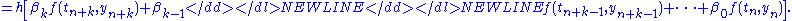
Another possibility is to use more points in the interval [tn,tn+1]. This leads to the family of Runge–Kutta methods, named after Carl Runge and Martin KuttaMartin Wilhelm KuttaMartin Wilhelm Kutta was a German mathematician.Kutta was born in Pitschen, Upper Silesia . He attended the University of Breslau from 1885 to 1890, and continued his studies in Munich until 1894, where he became the assistant of Walther Franz Anton von Dyck. From 1898, he spent a year at the...
. One of their fourth-order methods is especially popular.
Advanced features
A good implementation of one of these methods for solving an ODE entails more than the time-stepping formula.
It is often inefficient to use the same step size all the time, so variable step-size methods have been developed. Usually, the step size is chosen such that the (local) error per step is below some tolerance level. This means that the methods must also compute an error indicator, an estimate of the local error.
An extension of this idea is to choose dynamically between different methods of different orders (this is called a variable order method). Methods based on Richardson extrapolationRichardson extrapolationIn numerical analysis, Richardson extrapolation is a sequence acceleration method, used to improve the rate of convergence of a sequence. It is named after Lewis Fry Richardson, who introduced the technique in the early 20th century. In the words of Birkhoff and Rota, ".....
, such as the Bulirsch–Stoer algorithmBulirsch–Stoer algorithmIn numerical analysis, the Bulirsch–Stoer algorithm is a method for the numerical solution of ordinary differential equations which combines three powerful ideas: Richardson extrapolation, the use of rational function extrapolation in Richardson-type applications, and the modified midpoint method,...
, are often used to construct various methods of different orders.
Other desirable features include:- dense output: cheap numerical approximations for the whole integration interval, and not only at the points t0, t1, t2, ...
- event location: finding the times where, say, a particular function vanishes. This typically requires the use of a root-finding algorithmRoot-finding algorithmA root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
. - support for parallel computingParallel computingParallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
. - when used for integrating with respect to time, time reversibility
Alternative methods
Many methods do not fall within the framework discussed here. Some classes of alternative methods are:- multiderivative methods, which use not only the function f but also its derivatives. This class includes Hermite–Obreschkoff methods and Fehlberg methodsRunge–Kutta–Fehlberg methodIn mathematics, the Runge–Kutta–Fehlberg method is an algorithm of numerical analysis for the numerical solution of ordinary differential equations. It was developed by the German mathematician Erwin Fehlberg and is based on the class of Runge–Kutta methods...
, as well as methods like the Parker–Sochacki method or Bychkov-Scherbakov method, which compute the coefficients of the Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of the solution y recursively. - methods for second order ODEs. We said that all higher-order ODEs can be transformed to first-order ODEs of the form (1). While this is certainly true, it may not be the best way to proceed. In particular, Nyström methods work directly with second-order equations.
- geometric integration methodsGeometric integratorIn the mathematical field of numerical ordinary differential equations, a geometric integrator is a numerical method that preserves geometric properties of the exact flow of a differential equation.-Pendulum example:...
are especially designed for special classes of ODEs (e.g., symplectic integratorSymplectic integratorIn mathematics, a symplectic integrator is a numerical integration scheme for a specific group of differential equations related to classical mechanics and symplectic geometry. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations...
s for the solution of Hamiltonian equationsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
). They take care that the numerical solution respects the underlying structure or geometry of these classes.
Analysis
Numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
is not only the design of numerical methods, but also their analysis. Three central concepts in this analysis are:- convergence: whether the method approximates the solution,
- order: how well it approximates the solution, and
- stabilityNumerical stabilityIn the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
: whether errors are damped out.
Convergence
A numerical method is said to be convergent if the numerical solution approaches the exact solution as the step size h goes to 0. More precisely, we require that for every ODE (1) with a Lipschitz function f and every t* > 0,
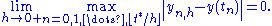
All the methods mentioned above are convergent. In fact, convergence is a condition sine qua nonSine qua nonSine qua non or condicio sine qua non refers to an indispensable and essential action, condition, or ingredient...
for any numerical scheme.
Consistency and order
Suppose the numerical method is
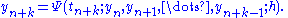
The local error of the method is the error committed by one step of the method. That is, it is the difference between the result given by the method, assuming that no error was made in earlier steps, and the exact solution:
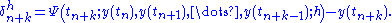
The method is said to be consistent if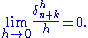
The method has order if
if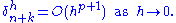
Hence a method is consistent if it has an order greater than 0. The (forward) Euler method (4) and the backward Euler method (6) introduced above both have order 1, so they are consistent. Most methods being used in practice attain higher order. Consistency is a necessary condition for convergence, but not sufficient; for a method to be convergent, it must be both consistent and zero-stable.
A related concept is the global error, the error sustained in all the steps one needs to reach a fixed time t. Explicitly, the global error at time t is yN − y(t) where N = (t−t0)/h. The global error of a pth order one-step method is O(hp); in particular, such a method is convergent. This statement is not necessarily true for multi-step methods.
Stability and stiffness
- Main article: Stiff equationStiff equationIn mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
For some differential equations, application of standard methods—such as the Euler method, explicit Runge–Kutta methodsRunge–Kutta methodsIn numerical analysis, the Runge–Kutta methods are an important family of implicit and explicit iterative methods for the approximation of solutions of ordinary differential equations. These techniques were developed around 1900 by the German mathematicians C. Runge and M.W. Kutta.See the article...
, or multistep methodMultistep methodLinear multistep methods are used for the numerical solution of ordinary differential equations. Conceptually, a numerical method starts from an initial point and then takes a short step forward in time to find the next solution point. The process continues with subsequent steps to map out the...
s (e.g., Adams–Bashforth methods)—exhibit instability in the solutions, though other methods may produce stable solutions. This "difficult behaviour" in the equation (which may not necessarily be complex itself) is described as stiffness, and is often caused by the presence of different time scales in the underlying problem. Stiff problems are ubiquitous in chemical kineticsChemical kineticsChemical kinetics, also known as reaction kinetics, is the study of rates of chemical processes. Chemical kinetics includes investigations of how different experimental conditions can influence the speed of a chemical reaction and yield information about the reaction's mechanism and transition...
, control theoryControl theoryControl theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, solid mechanicsSolid mechanicsSolid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
, weather forecastingWeather forecastingWeather forecasting is the application of science and technology to predict the state of the atmosphere for a given location. Human beings have attempted to predict the weather informally for millennia, and formally since the nineteenth century...
, biologyBiologyBiology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, plasma physics, and electronicsElectronicsElectronics is the branch of science, engineering and technology that deals with electrical circuits involving active electrical components such as vacuum tubes, transistors, diodes and integrated circuits, and associated passive interconnection technologies...
.
History
Below is a timelineChronologyChronology is the science of arranging events in their order of occurrence in time, such as the use of a timeline or sequence of events. It is also "the determination of the actual temporal sequence of past events".Chronology is part of periodization...
of some important developments in this field.
- 1768 - Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
publishes his method. - 1824 - Augustin Louis CauchyAugustin Louis CauchyBaron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
proves convergence of the Euler method. In this proof, Cauchy uses the implicit Euler method. - 1855 - First mention of the multistep methodMultistep methodLinear multistep methods are used for the numerical solution of ordinary differential equations. Conceptually, a numerical method starts from an initial point and then takes a short step forward in time to find the next solution point. The process continues with subsequent steps to map out the...
s of John Couch AdamsJohn Couch AdamsJohn Couch Adams was a British mathematician and astronomer. Adams was born in Laneast, near Launceston, Cornwall, and died in Cambridge. The Cornish name Couch is pronounced "cooch"....
in a letter written by F. Bashforth. - 1895 - Carl Runge publishes the first Runge–Kutta method.
- 1905 - Martin KuttaMartin Wilhelm KuttaMartin Wilhelm Kutta was a German mathematician.Kutta was born in Pitschen, Upper Silesia . He attended the University of Breslau from 1885 to 1890, and continued his studies in Munich until 1894, where he became the assistant of Walther Franz Anton von Dyck. From 1898, he spent a year at the...
describes the popular fourth-order Runge–Kutta method. - 1910 - Lewis Fry RichardsonLewis Fry RichardsonLewis Fry Richardson, FRS was an English mathematician, physicist, meteorologist, psychologist and pacifist who pioneered modern mathematical techniques of weather forecasting, and the application of similar techniques to studying the causes of wars and how to prevent them...
announces his extrapolation method, Richardson extrapolationRichardson extrapolationIn numerical analysis, Richardson extrapolation is a sequence acceleration method, used to improve the rate of convergence of a sequence. It is named after Lewis Fry Richardson, who introduced the technique in the early 20th century. In the words of Birkhoff and Rota, ".....
. - 1952 - Charles F. Curtiss and Joseph Oakland Hirschfelder coin the term stiff equationStiff equationIn mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
s.
See also
- Courant–Friedrichs–Lewy conditionCourant–Friedrichs–Lewy conditionIn mathematics, the Courant–Friedrichs–Lewy condition is a necessary condition for convergence while solving certain partial differential equations numerically by the method of finite differences. It arises when explicit time-marching schemes are used for the numerical solution...
- Energy driftEnergy driftIn molecular dynamics, orbit, and particle simulations, energy drift is the gradual change in the total energy of a closed system. According to the laws of mechanics, the energy should be a constant of motion and should not change...
- List of numerical analysis topics#Numerical ordinary differential equations
- Reversible reference system propagation algorithm
- Trapezoidal rule
External links
- Joseph W. Rudmin, Application of the Parker–Sochacki Method to Celestial Mechanics, 1998.
- Dominique Tournès, L'intégration approchée des équations différentielles ordinaires (1671-1914), thèse de doctorat de l'université Paris 7 - Denis Diderot, juin 1996. Réimp. Villeneuve d'Ascq : Presses universitaires du Septentrion, 1997, 468 p. (Extensive online material on ODE numerical analysis history, for English-language material on the history of ODE numerical analysis, see e.g. the paper books by Chabert and Goldstine quoted by him.)

