Wandering set
Encyclopedia
In those branches of mathematics
called dynamical system
s and ergodic theory
, the concept of a wandering set formalizes a certain idea of movement and mixing
in such systems. When a dynamical system has a wandering set of non-zero measure, then the system is a dissipative system
. This is very much the opposite of a conservative system, for which the ideas of the Poincaré recurrence theorem
apply. Intuitively, the connection between wandering sets and dissipation is easily understood: if a portion of the phase space
"wanders away" during normal time-evolution of the system, and is never visited again, then the system is dissipative. The language of wandering sets can be used to give a precise, mathematical definition to the concept of a dissipative system. The notion of wandering sets in phase space was introduced by Birkhoff
in 1927.
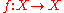of a topological space
X. A point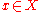
is said to be a wandering point if there is a neighbourhood
U of x and a positive integer N such that for all
, the iterated map is non-intersecting:
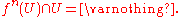
A handier definition requires only that the intersection have measure zero. To be precise, the definition requires that X be a measure space, i.e. part of a triple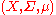
of Borel set
s
and a measure 
such that
Similarly, a continuous-time system will have a map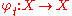
defining the time evolution or flow
of the system, with the time-evolution operator
being a one-parameter continuous abelian group
action
on X:
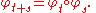
In such a case, a wandering point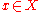
will have a neighbourhood
U of x and a time T such that for all times
, the time-evolved map is of measure zero:
These simpler definitions may be fully generalized to a general group
action
. Let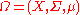
be a measure space, that is, a set with a measure
defined on its Borel subsets. Let
be a group
acting
on that set. Given a point
, the set
is called the trajectory
or orbit of the point x.
An element
is called a wandering point if there exists a neighborhood U of x and a neighborhood V of the identity in 
such that
for all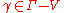
.
is non-wandering if, for every open set U containing x, one has that
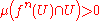
for some
and any 
arbitrarily large. Similar definitions follow for the continuous-time and discrete and continuous group actions.
is a wandering set under the action of a discrete group 
if W is measurable and if, for any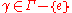 
the intersection
is a set of measure zero.
The concept of a wandering set is in a sense dual to the ideas expressed in the Poincaré recurrence theorem
. If there exists a wandering set of positive measure, then the action of
is said to be dissipative, and the dynamical system
is said to be a dissipative system
. If there is no such wandering set, the action is said to be conservative, and the system is a conservative system. For example, any system for which the Poincaré recurrence theorem holds cannot have, by definition, a wandering set of positive measure; and is thus an example of a conservative system.
Define the trajectory of a wandering set W as
The action of
is said to be completely dissipative if there exists a wandering set W of positive measure, such that the orbit 
is almost-everywhere equal to 
, that is, if
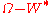
is a set of measure zero.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
called dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s and ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
, the concept of a wandering set formalizes a certain idea of movement and mixing
Mixing (mathematics)
In mathematics, mixing is an abstract concept originating from physics: the attempt to describe the irreversible thermodynamic process of mixing in the everyday world: mixing paint, mixing drinks, etc....
in such systems. When a dynamical system has a wandering set of non-zero measure, then the system is a dissipative system
Dissipative system
A dissipative system is a thermodynamically open system which is operating out of, and often far from, thermodynamic equilibrium in an environment with which it exchanges energy and matter....
. This is very much the opposite of a conservative system, for which the ideas of the Poincaré recurrence theorem
Poincaré recurrence theorem
In mathematics, the Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence. The result applies to physical systems in which...
apply. Intuitively, the connection between wandering sets and dissipation is easily understood: if a portion of the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
"wanders away" during normal time-evolution of the system, and is never visited again, then the system is dissipative. The language of wandering sets can be used to give a precise, mathematical definition to the concept of a dissipative system. The notion of wandering sets in phase space was introduced by Birkhoff
George David Birkhoff
-External links:* − from National Academies Press, by Oswald Veblen....
in 1927.
Wandering points
A common, discrete-time definition of wandering sets starts with a map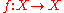 of a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X. A point
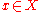is said to be a wandering point if there is a neighbourhoodNeighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
U of x and a positive integer N such that for all
, the iterated map is non-intersecting: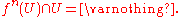A handier definition requires only that the intersection have measure zero. To be precise, the definition requires that X be a measure space, i.e. part of a triple
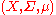of Borel setBorel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s
and a measure such thatSimilarly, a continuous-time system will have a map
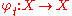defining the time evolution or flowFlow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
of the system, with the time-evolution operator
being a one-parameter continuous abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on X:
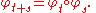
In such a case, a wandering point
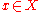will have a neighbourhoodNeighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
U of x and a time T such that for all times
, the time-evolved map is of measure zero:These simpler definitions may be fully generalized to a general group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. Let
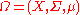be a measure space, that is, a set with a measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
defined on its Borel subsets. Let
be a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on that set. Given a point
, the setis called the trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
or orbit of the point x.
An element
is called a wandering point if there exists a neighborhood U of x and a neighborhood V of the identity in such thatfor all
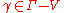.Non-wandering points
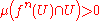
The definition for a non-wandering point is in a sense the converse. In the discrete case, is non-wandering if, for every open set U containing x, one has thatfor some
and any arbitrarily large. Similar definitions follow for the continuous-time and discrete and continuous group actions.Wandering sets and dissipative systems
A wandering set is a collection of wandering points. More precisely, a subset W of is a wandering set under the action of a discrete group if W is measurable and if, for any 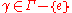the intersectionis a set of measure zero.
The concept of a wandering set is in a sense dual to the ideas expressed in the Poincaré recurrence theorem
Poincaré recurrence theorem
In mathematics, the Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence. The result applies to physical systems in which...
. If there exists a wandering set of positive measure, then the action of
is said to be dissipative, and the dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
is said to be a dissipative systemDissipative system
A dissipative system is a thermodynamically open system which is operating out of, and often far from, thermodynamic equilibrium in an environment with which it exchanges energy and matter....
. If there is no such wandering set, the action is said to be conservative, and the system is a conservative system. For example, any system for which the Poincaré recurrence theorem holds cannot have, by definition, a wandering set of positive measure; and is thus an example of a conservative system.
Define the trajectory of a wandering set W as
The action of
is said to be completely dissipative if there exists a wandering set W of positive measure, such that the orbit is almost-everywhere equal to , that is, if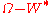is a set of measure zero.