
Kleetope
Encyclopedia
In geometry
and polyhedral combinatorics
, the Kleetope of a polyhedron
or higher-dimensional convex polytope
is another polyhedron or polytope formed by replacing each facet of with a shallow pyramid
. Kleetopes are named after Victor Klee
.
is the Kleetope of a tetrahedron
, the triakis octahedron
is the Kleetope of an octahedron
, and the triakis icosahedron
is the Kleetope of an icosahedron
. In each of these cases the Kleetope is formed by adding a triangular pyramid to each face of the original polyhedron. Conway
generalizes Kepler's kis prefix as this same kis operator.
The tetrakis hexahedron
is the Kleetope of the cube
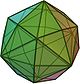
, formed by adding a square pyramid to each of its faces, and the pentakis dodecahedron
is the Kleetope of the dodecahedron, formed by adding a pentagonal pyramid to each face of the dodecahedron.
The base polyhedron of a Kleetope does not need to be a Platonic solid
. For instance, the disdyakis dodecahedron
is the Kleetope of the rhombic dodecahedron
, formed by replacing each rhombus
face of the dodecahedron by a rhombic pyramid, and the disdyakis triacontahedron
is the Kleetope of the rhombic triacontahedron
. In fact, the base polyhedron of a Kleetope does not need to be Face-transitive, as can be seen from the tripentakis icosidodecahedron above.
The Goldner–Harary graph
may be represented as the graph of vertices and edges of the Kleetope of the triangular bipyramid.
The base polyhedron of a Kleetope does not even need to be convex
, viz.
of the union of the vertices of and the set of new vertices.
Alternatively, the Kleetope may be defined by duality
and its dual operation, truncation
: the Kleetope of is the dual polyhedron
of the truncation of the dual of .
If every -dimensional face of a -dimensional polytope is a simplex
, and if , then every -dimensional face of is also a simplex. In particular, the Kleetope of any three-dimensional polyhedron is a simplicial polyhedron
, a polyhedron in which all facets are triangles.
Kleetopes may be used to generate polyhedra that do not have any Hamiltonian cycles: any path through one of the vertices added in the Kleetope construction must go into and out of the vertex through its neighbors in the original polyhedron, and if there are more new vertices than original vertices then there are not enough neighbors to go around. In particular, the Goldner–Harary graph
, the Kleetope of the triangular bipyramid, has six vertices added in the Kleetope construction and only five in the bipyramid from which it was formed, so it is non-Hamiltonian; it is the simplest possible non-Hamiltonian simplicial polyhedron. If a polyhedron with vertices is formed by repeating the Kleetope construction some number of times, starting from a tetrahedron, then its longest path has length ; that is, the shortness exponent of these graphs is , approximately 0.630930. The same technique shows that in any higher dimension , there exist simplicial polytopes with shortness exponent . Similarly, used the Kleetope construction to provide an infinite family of examples of simplicial polyhedra with an even number of vertices that have no perfect matching.
Kleetopes also have some extreme properties related to their vertex degrees
: if each edge in a planar graph
is incident to at least seven other edges, then there must exist a vertex of degree at most five all but one of whose neighbors have degree 20 or more, and the Kleetope of the Kleetope of the icosahedron provides an example in which the high-degree vertices have degree exactly 20.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and polyhedral combinatorics
Polyhedral combinatorics
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher dimensional convex polytopes....
, the Kleetope of a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
or higher-dimensional convex polytope
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
is another polyhedron or polytope formed by replacing each facet of with a shallow pyramid
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
. Kleetopes are named after Victor Klee
Victor Klee
Victor L. Klee, Jr. was a mathematician specialising in convex sets, functional analysis, analysis of algorithms, optimization, and combinatorics. He spent almost his entire career at the University of Washington in Seattle.Born in San Francisco, Vic Klee earned his B.A...
.
Examples
The triakis tetrahedronTriakis tetrahedron
In geometry, a triakis tetrahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated tetrahedron.It can be seen as a tetrahedron with triangular pyramids added to each face; that is, it is the Kleetope of the tetrahedron...
is the Kleetope of a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, the triakis octahedron
Triakis octahedron
In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a trisoctahedron, or, more...
is the Kleetope of an octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, and the triakis icosahedron
Triakis icosahedron
In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.It can be seen as an icosahedron with triangular pyramids augmented to each face; that is, it is the Kleetope of the icosahedron...
is the Kleetope of an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
. In each of these cases the Kleetope is formed by adding a triangular pyramid to each face of the original polyhedron. Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
generalizes Kepler's kis prefix as this same kis operator.
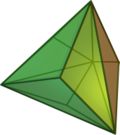 The triakis tetrahedron Triakis tetrahedron In geometry, a triakis tetrahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated tetrahedron.It can be seen as a tetrahedron with triangular pyramids added to each face; that is, it is the Kleetope of the tetrahedron... , the Kleetope of the tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... . |
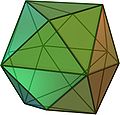 The tetrakis hexahedron Tetrakis hexahedron In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid. It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube.... , the Kleetope of the cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... . |
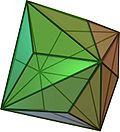 The triakis octahedron Triakis octahedron In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a trisoctahedron, or, more... , the Kleetope of the octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... . |
 The pentakis dodecahedron Pentakis dodecahedron In geometry, a pentakis dodecahedron is a Catalan solid. Its dual is the truncated icosahedron, an Archimedean solid.It can be seen as a dodecahedron with a pentagonal pyramid covering each face; that is, it is the Kleetope of the dodecahedron... , the Kleetope of the dodecahedron. |
 The triakis icosahedron Triakis icosahedron In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.It can be seen as an icosahedron with triangular pyramids augmented to each face; that is, it is the Kleetope of the icosahedron... , the Kleetope of the icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... . |
The tetrakis hexahedron
Tetrakis hexahedron
In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid. It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube....
is the Kleetope of the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, formed by adding a square pyramid to each of its faces, and the pentakis dodecahedron
Pentakis dodecahedron
In geometry, a pentakis dodecahedron is a Catalan solid. Its dual is the truncated icosahedron, an Archimedean solid.It can be seen as a dodecahedron with a pentagonal pyramid covering each face; that is, it is the Kleetope of the dodecahedron...
is the Kleetope of the dodecahedron, formed by adding a pentagonal pyramid to each face of the dodecahedron.
 The disdyakis dodecahedron Disdyakis dodecahedron In geometry, a disdyakis dodecahedron, or hexakis octahedron, is a Catalan solid and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons... , the Kleetope of the rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... . |
 The disdyakis triacontahedron Disdyakis triacontahedron In geometry, a disdyakis triacontahedron, or hexakis icosahedron is a Catalan solid and the dual to the Archimedean truncated icosidodecahedron. As such it is face uniform but with irregular face polygons... , the Kleetope of the rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron.... . |
The tripentakis icosidodecahedron, the Kleetope of the icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... . |
The base polyhedron of a Kleetope does not need to be a Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
. For instance, the disdyakis dodecahedron
Disdyakis dodecahedron
In geometry, a disdyakis dodecahedron, or hexakis octahedron, is a Catalan solid and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons...
is the Kleetope of the rhombic dodecahedron
Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
, formed by replacing each rhombus
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
face of the dodecahedron by a rhombic pyramid, and the disdyakis triacontahedron
Disdyakis triacontahedron
In geometry, a disdyakis triacontahedron, or hexakis icosahedron is a Catalan solid and the dual to the Archimedean truncated icosidodecahedron. As such it is face uniform but with irregular face polygons...
is the Kleetope of the rhombic triacontahedron
Rhombic triacontahedron
In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
. In fact, the base polyhedron of a Kleetope does not need to be Face-transitive, as can be seen from the tripentakis icosidodecahedron above.
The Goldner–Harary graph
Goldner–Harary graph
In the mathematical field of graph theory, the Goldner–Harary graph is a simple undirected graph with 11 vertices and 27 edges. It is named after A. Goldner and Frank Harary, who proved in 1975 that it was the smallest non-Hamiltonian maximal planar graph...
may be represented as the graph of vertices and edges of the Kleetope of the triangular bipyramid.
The base polyhedron of a Kleetope does not even need to be convex
Convex
'The word convex means curving out or bulging outward, as opposed to concave. Convex or convexity may refer to:Mathematics:* Convex set, a set of points containing all line segments between each pair of its points...
, viz.
The small stellapentakis dodecahedron Small stellapentakis dodecahedron In geometry, the small stellapentakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the truncated great dodecahedron. It has 60 intersecting triangular faces.- External links :*... , the Kleetope of the small stellated dodecahedron. |
The great stellapentakis dodecahedron Great stellapentakis dodecahedron In geometry, the great stellapentakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the truncated great icosahedron. It has 60 intersecting triangular faces.- External links :*... , the Kleetope of the great stellated dodecahedron. |
The great pentakis dodecahedron Great pentakis dodecahedron In geometry, the great pentakis dodecahedron is a nonconvex isohedral polyhedron.It is the dual of the uniform small stellated truncated dodecahedron. The decagrammic faces pass close to the origin in the uniform polyhedron, causing this dual to be very spikey.... , the Kleetope of the great dodecahedron. |
The great triakis icosahedron Great triakis icosahedron In geometry, the great triakis icosahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great stellated truncated dodecahedron.... , the Kleetope of the great icosahedron. |
Definitions
One method of forming the Kleetope of a polytope is to place a new vertex outside , near the centroid of each facet. If all of these new vertices are placed close enough to the corresponding centroids, then the only other vertices visible to them will be the vertices of the facets from which they are defined. In this case, the Kleetope of is the convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the union of the vertices of and the set of new vertices.
Alternatively, the Kleetope may be defined by duality
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
and its dual operation, truncation
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
: the Kleetope of is the dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of the truncation of the dual of .
Properties and applications
If has enough vertices relative to its dimension, then the Kleetope of is dimensionally unambiguous: the graph formed by its edges and vertices is not the graph of a different polyhedron or polytope with a different dimension. More specifically, if the number of vertices of a -dimensional polytope is at least , then is dimensionally unambiguous.If every -dimensional face of a -dimensional polytope is a simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, and if , then every -dimensional face of is also a simplex. In particular, the Kleetope of any three-dimensional polyhedron is a simplicial polyhedron
Simplicial polytope
In geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....
, a polyhedron in which all facets are triangles.
Kleetopes may be used to generate polyhedra that do not have any Hamiltonian cycles: any path through one of the vertices added in the Kleetope construction must go into and out of the vertex through its neighbors in the original polyhedron, and if there are more new vertices than original vertices then there are not enough neighbors to go around. In particular, the Goldner–Harary graph
Goldner–Harary graph
In the mathematical field of graph theory, the Goldner–Harary graph is a simple undirected graph with 11 vertices and 27 edges. It is named after A. Goldner and Frank Harary, who proved in 1975 that it was the smallest non-Hamiltonian maximal planar graph...
, the Kleetope of the triangular bipyramid, has six vertices added in the Kleetope construction and only five in the bipyramid from which it was formed, so it is non-Hamiltonian; it is the simplest possible non-Hamiltonian simplicial polyhedron. If a polyhedron with vertices is formed by repeating the Kleetope construction some number of times, starting from a tetrahedron, then its longest path has length ; that is, the shortness exponent of these graphs is , approximately 0.630930. The same technique shows that in any higher dimension , there exist simplicial polytopes with shortness exponent . Similarly, used the Kleetope construction to provide an infinite family of examples of simplicial polyhedra with an even number of vertices that have no perfect matching.
Kleetopes also have some extreme properties related to their vertex degrees
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
: if each edge in a planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
is incident to at least seven other edges, then there must exist a vertex of degree at most five all but one of whose neighbors have degree 20 or more, and the Kleetope of the Kleetope of the icosahedron provides an example in which the high-degree vertices have degree exactly 20.

