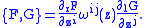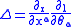Supermanifold
Encyclopedia
In physics
and mathematics
, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry
. Several definitions are in use, some of which are described below.
with both boson
ic and fermion
ic coordinates. These coordinates are usually denoted by

where x is the usual spacetime
vector, and and
and  are Grassmann-valued spinors.
are Grassmann-valued spinors.
Whether these extra coordinates have any physical meaning is debatable. However this formalism is very useful for writing down supersymmetric Lagrangian
s.
, the local structure of supermanifolds make them better suited to study with the tools of standard differential geometry and locally ringed spaces.
A supermanifold M of dimension (p,q) is a topological space
M with a sheaf
of superalgebra
s, usually denoted OM or C∞(M), that is locally isomorphic to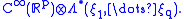
Note that the definition of a supermanifold is similar to that of a differentiable manifold
, except that the model space Rp has been replaced by the model superspace Rp|q.
An alternative approach to the dual point of view is to use the functor of points.
If M is a supermanifold of dimension (p,q), then the underlying space M inherits the structure of a differentiable manifold whose sheaf of smooth functions is OM/I, where I is the ideal
generated by all odd functions. Thus M is called the underlying space, or the body, of M. The quotient map OM → OM/I corresponds to an injective map M → M; thus M is a submanifold of M.
The proof of Batchelor's theorem relies in an essential way on the existence of a partition of unity, so it does not hold for complex or real-analytic supermanifolds.
. All natural geometric objects on a supermanifold are graded. In particular, the bundle of two-forms is equipped with a grading. An odd symplectic form ω on a supermanifold is a closed, odd form, inducing a non-degenerate pairing on TM. Such a supermanifold is called a P-manifold. Its graded dimension is necessarily (n,n), because the odd symplectic form induces a pairing of odd and even variables. There is a version of the Darboux theorem for P-manifolds, which allows one
to equip a P-manifold locally with a set of coordinates where the odd symplectic form ω is written as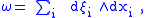
where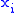 are even coordinates, and
are even coordinates, and 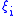 odd coordinates. (An odd symplectic form should not be confused with a Grassmann-even symplectic form
odd coordinates. (An odd symplectic form should not be confused with a Grassmann-even symplectic form
on a supermanifold. In contrast, the Darboux version of an even symplectic form is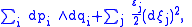
where are even coordinates,
are even coordinates, 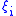 odd coordinates and
odd coordinates and 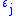 are either +1 or -1.)
are either +1 or -1.)
known as the antibracket of any two functions F and G on a supermanifold by
Here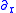 and
and 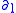 are the right and left derivative
are the right and left derivative
s respectively and z are the coordinates of the supermanifold. Equipped with this bracket, the algebra of functions on a supermanifold becomes an antibracket algebra
.
A coordinate transformation that preserves the antibracket is called a P-transformation. If the Berezinian
of a P-transformation is equal to one then it is called an SP-transformation.
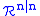 glued together by P-transformations. A manifold is said to be an SP-manifold if these transition functions can be chosen to be SP-transformations. Equivalently one may define an SP-manifold as a supermanifold with a nondegenerate odd 2-form ω and a density function ρ such that on each coordinate patch there exist Darboux coordinates in which ρ is identically equal to one.
glued together by P-transformations. A manifold is said to be an SP-manifold if these transition functions can be chosen to be SP-transformations. Equivalently one may define an SP-manifold as a supermanifold with a nondegenerate odd 2-form ω and a density function ρ such that on each coordinate patch there exist Darboux coordinates in which ρ is identically equal to one.
of the corresponding Hamiltonian vector field
. Explicitly one defines
In Darboux coordinates this definition reduces to
where xa and θa are even and odd coordinates such that
The Laplacian is odd and nilpotent
One may define the cohomology
of functions H with respect to the Laplacian. In Geometry of Batalin-Vilkovisky quantization, Albert Schwarz
has proven that the integral of a function H over a Lagrangian submanifold L depends only on the cohomology class of H and on the homology
class of the body of L in the body of the ambient supermanifold.
(n,m) is an odd m-dimensional
distribution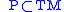 .
.
With such a distribution one associates
its Frobenius tensor
(since P is odd, the skew-symmetric Frobenius
tensor is a symmetric operation).
If this tensor is non-degenerate,
e.g. lies in an open orbit of
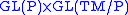 ,
,
M is called a SUSY-manifold.
SUSY-structure in dimension (1, k)
is the same as odd contact structure.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
. Several definitions are in use, some of which are described below.
Physics
In physics, a supermanifold is a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
with both boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
ic and fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic coordinates. These coordinates are usually denoted by

where x is the usual spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
vector, and
 and
and  are Grassmann-valued spinors.
are Grassmann-valued spinors.Whether these extra coordinates have any physical meaning is debatable. However this formalism is very useful for writing down supersymmetric Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
s.
Supermanifold: a definition
Although supermanifolds are special cases of noncommutative manifoldsNoncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
, the local structure of supermanifolds make them better suited to study with the tools of standard differential geometry and locally ringed spaces.
A supermanifold M of dimension (p,q) is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
M with a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
s, usually denoted OM or C∞(M), that is locally isomorphic to
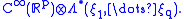
Note that the definition of a supermanifold is similar to that of a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, except that the model space Rp has been replaced by the model superspace Rp|q.
Side comment
This is different from the alternative definition where, using a fixed Grassmann algebra generated by a countable number of generators Λ, one defines a supermanifold as a point set space using charts with the "even coordinates" taking values in the linear combination of elements of Λ with even grading and the "odd coordinates" taking values which are linear combinations of elements of Λ with odd grading. This raises the question of the physical meaning of all these Grassmann-valued variables. Many physicists claim that they have none and that they are purely formal; if this is the case, this may make the definition in the main part of the article preferable.Properties
Unlike a regular manifold, a supermanifold is not entirely composed of a set of points. Instead, one takes the dual point of view that the structure of a supermanifold M is contained in its sheaf OM of "smooth functions". In the dual point of view, an injective map corresponds to a surjection of sheaves, and a surjective map corresponds to an injection of sheaves.An alternative approach to the dual point of view is to use the functor of points.
If M is a supermanifold of dimension (p,q), then the underlying space M inherits the structure of a differentiable manifold whose sheaf of smooth functions is OM/I, where I is the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by all odd functions. Thus M is called the underlying space, or the body, of M. The quotient map OM → OM/I corresponds to an injective map M → M; thus M is a submanifold of M.
Examples
- Let M be a manifold. The odd tangent bundle ΠTM is a supermanifold given by the sheaf Ω(M) of differential forms on M.
- More generally, let E → M be a vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
. Then ΠE is a supermanifold given by the sheaf Γ(ΛE*). In fact, Π is a functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category of vector bundles to the category of supermanifolds.
- Lie supergroupsSupergroup (physics)The concept of supergroup is a generalization of that of group. In other words, every group is a supergroup but not every supergroup is a group. A supergroup is like a Lie group in that there is a well defined notion of smooth function defined on them....
are examples of supermanifolds.
Batchelor's theorem
Batchelor's theorem states that every supermanifold is noncanonically isomorphic to a supermanifold of the form ΠE. The word "noncanonically" prevents one from concluding that supermanifolds are simply glorified vector bundles; although the functor Π maps surjectively onto the isomorphism classes of supermanifolds, it is not an equivalence of categories.The proof of Batchelor's theorem relies in an essential way on the existence of a partition of unity, so it does not hold for complex or real-analytic supermanifolds.
Odd symplectic form
In many physical and geometric applications, a supermanifold comes equipped with an Grassmann-odd symplectic structureSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
. All natural geometric objects on a supermanifold are graded. In particular, the bundle of two-forms is equipped with a grading. An odd symplectic form ω on a supermanifold is a closed, odd form, inducing a non-degenerate pairing on TM. Such a supermanifold is called a P-manifold. Its graded dimension is necessarily (n,n), because the odd symplectic form induces a pairing of odd and even variables. There is a version of the Darboux theorem for P-manifolds, which allows one
to equip a P-manifold locally with a set of coordinates where the odd symplectic form ω is written as
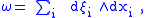
where
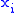 are even coordinates, and
are even coordinates, and 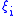 odd coordinates. (An odd symplectic form should not be confused with a Grassmann-even symplectic form
odd coordinates. (An odd symplectic form should not be confused with a Grassmann-even symplectic formSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
on a supermanifold. In contrast, the Darboux version of an even symplectic form is
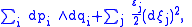
where
 are even coordinates,
are even coordinates, 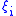 odd coordinates and
odd coordinates and 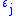 are either +1 or -1.)
are either +1 or -1.)Antibracket
Given an odd symplectic 2-form ω one may define a Poisson bracketPoisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
known as the antibracket of any two functions F and G on a supermanifold by
Here
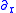 and
and 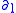 are the right and left derivative
are the right and left derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s respectively and z are the coordinates of the supermanifold. Equipped with this bracket, the algebra of functions on a supermanifold becomes an antibracket algebra
Antibracket algebra
In mathematics and theoretical physics, a Gerstenhaber algebra is an algebraic structure discovered by Murray Gerstenhaber that combines the structures of a supercommutative ring and a graded Lie superalgebra...
.
A coordinate transformation that preserves the antibracket is called a P-transformation. If the Berezinian
Berezinian
In mathematics and theoretical physics, the Berezinian or superdeterminant is a generalization of the determinant to the case of supermatrices. The name is for Felix Berezin...
of a P-transformation is equal to one then it is called an SP-transformation.
P and SP-manifolds
Using the Darboux theorem for odd symplectic forms one can show that P-manifolds are constructed from open sets of superspaces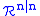 glued together by P-transformations. A manifold is said to be an SP-manifold if these transition functions can be chosen to be SP-transformations. Equivalently one may define an SP-manifold as a supermanifold with a nondegenerate odd 2-form ω and a density function ρ such that on each coordinate patch there exist Darboux coordinates in which ρ is identically equal to one.
glued together by P-transformations. A manifold is said to be an SP-manifold if these transition functions can be chosen to be SP-transformations. Equivalently one may define an SP-manifold as a supermanifold with a nondegenerate odd 2-form ω and a density function ρ such that on each coordinate patch there exist Darboux coordinates in which ρ is identically equal to one.Laplacian
One may define a Laplacian operator Δ on an SP-manifold as the operator which takes a function H to one half of the divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the corresponding Hamiltonian vector field
Hamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
. Explicitly one defines
-
-
 .
.
-
In Darboux coordinates this definition reduces to
where xa and θa are even and odd coordinates such that
-
-
-
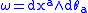 .
.
-
-
The Laplacian is odd and nilpotent
-
-
-
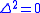 .
.
-
-
One may define the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of functions H with respect to the Laplacian. In Geometry of Batalin-Vilkovisky quantization, Albert Schwarz
Albert Schwarz
Albert S. Schwarz is a mathematician and a theoretical physicist educated in Soviet Union and now a Professor at the University of California-Davis. He is one of the pioneers of Morse theory and brought up the first example of a topological quantum field theory. Schwarz worked on some examples in...
has proven that the integral of a function H over a Lagrangian submanifold L depends only on the cohomology class of H and on the homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
class of the body of L in the body of the ambient supermanifold.
SUSY
A pre-SUSY-structure on a supermanifold of dimension(n,m) is an odd m-dimensional
distribution
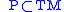 .
.With such a distribution one associates
its Frobenius tensor

(since P is odd, the skew-symmetric Frobenius
tensor is a symmetric operation).
If this tensor is non-degenerate,
e.g. lies in an open orbit of
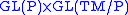 ,
,M is called a SUSY-manifold.
SUSY-structure in dimension (1, k)
is the same as odd contact structure.
See also
- SupersymmetrySupersymmetryIn particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
- SupergeometrySupergeometrySupergeometry is differential geometry of modules over graded commutative algebras, supermanifolds and graded manifolds. Supergeometry is part and parcel of many classical and quantum field theories involving odd fields, e.g., SUSY field theory, BRST theory, or supergravity.Supergeometry is...
- Graded manifoldGraded manifoldGraded manifolds are extensions of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra. Graded manifolds are not supermanifolds though there is a certain correspondence between the graded manifolds and the DeWitt supermanifolds. Both graded manifolds and...
- Batalin–Vilkovisky formalism
External links
- Super manifolds at the Manifold Atlas.