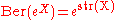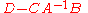Berezinian
Encyclopedia
In mathematics
and theoretical physics
, the Berezinian or superdeterminant is a generalization of the determinant
to the case of supermatrices
. The name is for Felix Berezin
. The Berezinian plays a role analogous to the determinant when considering coordinate changes for integration on a supermanifold
.
where str(X) denotes the supertrace
of X. Unlike the classical determinant, the Berezinian is defined only for invertible supermatrices.
The simplest case to consider is the Berezinian of a supermatrix with entries in a field
K. Such supermatrices represent linear transformation
s of a super vector space
over K. A particular even supermatrix is a block matrix
of the form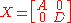
Such a matrix is invertible if and only if
both A and D are invertible matrices over K. The Berezinian of X is given by
For a motivation of the negative exponent see the substitution formula in the odd case.
More generally, consider matrices with entries in a supercommutative algebra
R. An even supermatrix is then of the form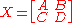
where A and D have even entries and B and C have odd entries. Such a matrix is invertible if and only if both A and D are invertible in the commutative ring
R0 (the even subalgebra of R). In this case the Berezinian is given by
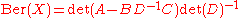
or, equivalently, by
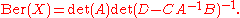
These formulas are well-defined since we are only taking determinants of matrices whose entries are in the commutative ring R0. The matrix
is known as the Schur complement
of A relative to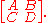
An odd matrix X can only be invertible if the number of even dimensions equals the number of odd dimensions. In this case, invertibility of X is equivalent to the invertibility of JX, where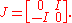
Then the Berezinian of X is defined as
Suppose that M is a free module of dimension (p,q) over R. Let A be the (super)symmetric algebra S*(M*) of the dual M* of M. Then an automorphism of M acts on the ext
module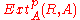
(which has dimension (1,0) if q is even and dimension (0,1) if q is odd))
as multiplication by the Berezianian.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the Berezinian or superdeterminant is a generalization of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
to the case of supermatrices
Supermatrix
In mathematics and theoretical physics, a supermatrix is a Z2-graded analog of an ordinary matrix. Specifically, a supermatrix is a 2×2 block matrix with entries in a superalgebra...
. The name is for Felix Berezin
Felix Berezin
Felix Alexandrovich Berezin was a Soviet Russian mathematician and physicist known for his contributions to the theory of supersymmetry and supermanifolds as well as to the path integral formulation of quantum field theory....
. The Berezinian plays a role analogous to the determinant when considering coordinate changes for integration on a supermanifold
Supermanifold
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
.
Definition
The Berezinian is uniquely determined by two defining properties:
where str(X) denotes the supertrace
Supertrace
In the theory of superalgebras, if A is a commutative superalgebra, V is a free right A-supermodule and T is an endomorphism from V to itself, then the supertrace of T, str is defined by the following trace diagram:...
of X. Unlike the classical determinant, the Berezinian is defined only for invertible supermatrices.
The simplest case to consider is the Berezinian of a supermatrix with entries in a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K. Such supermatrices represent linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s of a super vector space
Super vector space
In mathematics, a super vector space is another name for a Z2-graded vector space, that is, a vector space over a field K with a given decompositionV=V_0\oplus V_1....
over K. A particular even supermatrix is a block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
of the form
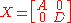
Such a matrix is invertible if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
both A and D are invertible matrices over K. The Berezinian of X is given by
For a motivation of the negative exponent see the substitution formula in the odd case.
More generally, consider matrices with entries in a supercommutative algebra
Supercommutative algebra
In mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
R. An even supermatrix is then of the form
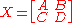
where A and D have even entries and B and C have odd entries. Such a matrix is invertible if and only if both A and D are invertible in the commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R0 (the even subalgebra of R). In this case the Berezinian is given by
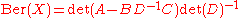
or, equivalently, by
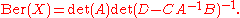
These formulas are well-defined since we are only taking determinants of matrices whose entries are in the commutative ring R0. The matrix
is known as the Schur complement
Schur complement
In linear algebra and the theory of matrices,the Schur complement of a matrix block is defined as follows.Suppose A, B, C, D are respectivelyp×p, p×q, q×p...
of A relative to
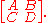
An odd matrix X can only be invertible if the number of even dimensions equals the number of odd dimensions. In this case, invertibility of X is equivalent to the invertibility of JX, where
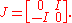
Then the Berezinian of X is defined as
Properties
- The Berezinian of X is always a unitUnit (ring theory)In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in the ring R0.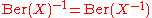 
where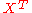 
denotes the supertranspose of X.
Berezinian module
The determinant of an endomorphism of a free module M can be defined as the induced action on the 1-dimensional highest exterior power of M. In the supersymmetric case there is no highest exterior power, but there is a still a similar definition of the Berezinian as follows.Suppose that M is a free module of dimension (p,q) over R. Let A be the (super)symmetric algebra S*(M*) of the dual M* of M. Then an automorphism of M acts on the ext
Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
module
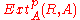
(which has dimension (1,0) if q is even and dimension (0,1) if q is odd))
as multiplication by the Berezianian.