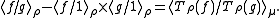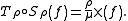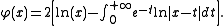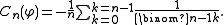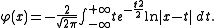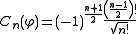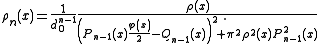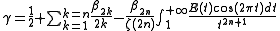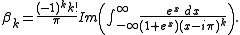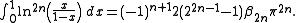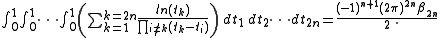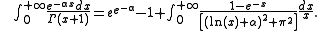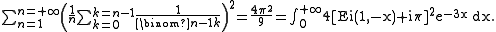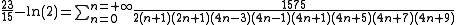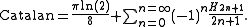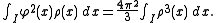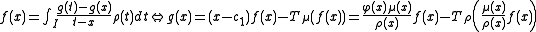Secondary measure
Encyclopedia
In mathematics, the secondary measure associated with a measure
of positive density
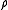 when there is one, is a measure of positive density
when there is one, is a measure of positive density 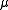 , turning the secondary polynomials associated with the orthogonal polynomials
, turning the secondary polynomials associated with the orthogonal polynomials
for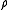 into an orthogonal system.
into an orthogonal system.
For example if one works in the Hilbert space
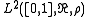
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
of positive density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
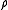 when there is one, is a measure of positive density
when there is one, is a measure of positive density 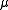 , turning the secondary polynomials associated with the orthogonal polynomials
, turning the secondary polynomials associated with the orthogonal polynomialsOrthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
for
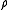 into an orthogonal system.
into an orthogonal system.Introduction
Under certain assumptions that we will specify further, it is possible to obtain the existence of a secondary measure and even to express it.For example if one works in the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
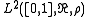
-

with
-
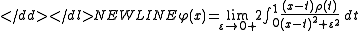
in the general case,
or:
-
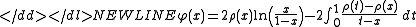
when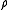 satisfy a LipschitzLipschitz- People :Lipschitz is a surname, which may be derived from the Polish city of Głubczyce , and may refer to:* Daniel Lipšic, Minister of Interior in Slovakia* Dr...
satisfy a LipschitzLipschitz- People :Lipschitz is a surname, which may be derived from the Polish city of Głubczyce , and may refer to:* Daniel Lipšic, Minister of Interior in Slovakia* Dr...
condition.
This application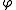 is called the reducer of
is called the reducer of 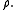
More generally,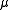 et
et 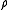 are linked by their Stieltjes transformation with the following formula:
are linked by their Stieltjes transformation with the following formula:
-
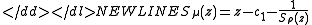
in which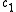 is the momentMoment- Science, engineering, and mathematics :* Moment , used in probability theory and statistics* Moment , several related concepts, including:** Angular momentum or moment of momentum, the rotational analog of momentum...
is the momentMoment- Science, engineering, and mathematics :* Moment , used in probability theory and statistics* Moment , several related concepts, including:** Angular momentum or moment of momentum, the rotational analog of momentum...
of order 1 of the measure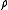 .
.
These secondary measures, and the theory around them, lead to some surprising results, and make it possible to find in an elegant way quite a few traditional formulas of analysis, mainly around the Euler Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, Riemann Zeta function, and Euler's constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
.
They also allowed the clarification of integrals and series with a tremendous effectiveness, though it is a priori difficult.
Finally they make it possible to solve integral equations of the form
-
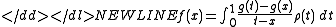
where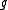 is the unknown function, and lead to theorems of convergence towards the Chebyshev and Dirac measures.
is the unknown function, and lead to theorems of convergence towards the Chebyshev and Dirac measures.
The broad outlines of the theory
Let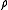 be a measure of positive densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
be a measure of positive densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
on an interval I and admitting moments of any order. We can build a family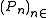 of orthogonal polynomialsOrthogonal polynomialsIn mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
of orthogonal polynomialsOrthogonal polynomialsIn mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
for the inner product induced by .
.
Let us call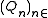 the sequence of the secondary polynomials associated with the family
the sequence of the secondary polynomials associated with the family 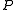 .
.
Under certain conditions there is a measure for which the family Q is orthogonal. This measure, which we can clarify from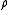 is called a secondary measure associated initial measure
is called a secondary measure associated initial measure 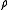 .
.
When is a probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is a probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
, a sufficient condition so that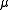 , while admitting moments of any order can be a secondary measure associated with
, while admitting moments of any order can be a secondary measure associated with 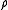 is that its Stieltjes Transformation is given by an equality of the type:
is that its Stieltjes Transformation is given by an equality of the type:
 is an arbitrary constant and
is an arbitrary constant and 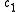 indicating the moment of order 1 of
indicating the moment of order 1 of 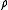 .
.
For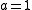 we obtain the measure known as secondary, remarkable since for
we obtain the measure known as secondary, remarkable since for  the normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
the normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of the polynomial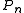 for
for  coincides exactly with the norm of the secondary polynomial associated
coincides exactly with the norm of the secondary polynomial associated  when using the measure
when using the measure 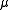 .
.
In this paramount case, and if the space generated by the orthogonal polynomials is dense in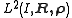 , the operator
, the operator 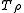 defined by
defined by 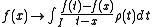 creating the secondary polynomials can be furthered to a linear map connecting space
creating the secondary polynomials can be furthered to a linear map connecting space 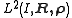 to
to  and becomes isometric if limited to the hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
and becomes isometric if limited to the hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
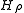 of the orthogonal functions with
of the orthogonal functions with  .
.
For unspecified functions square integrable for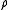 we obtain the more general formula of covarianceCovarianceIn probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
we obtain the more general formula of covarianceCovarianceIn probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
:
The theory continues by introducing the concept of reducible measure, meaning that the quotient is element of
is element of 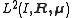 . The following results are then established:
. The following results are then established:
The reducer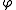 of
of 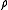 is an antecedent of
is an antecedent of 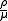 for the operator
for the operator  . (In fact the only antecedent which belongs to
. (In fact the only antecedent which belongs to 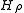 ).
).
For any function square integrable for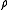 , there is an equality known as the reducing formula:
, there is an equality known as the reducing formula: 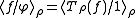 .
.
The operator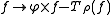 defined on the polynomials is prolonged in an isometryIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
defined on the polynomials is prolonged in an isometryIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
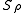 linking the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
linking the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the space of these polynomials in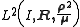 to the hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
to the hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
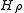 provided with the norm induced by
provided with the norm induced by 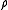 .
.
Under certain restrictive conditions the operator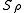 acts like the adjointAdjointIn mathematics, the term adjoint applies in several situations. Several of these share a similar formalism: if A is adjoint to B, then there is typically some formula of the type = .Specifically, adjoint may mean:...
acts like the adjointAdjointIn mathematics, the term adjoint applies in several situations. Several of these share a similar formalism: if A is adjoint to B, then there is typically some formula of the type = .Specifically, adjoint may mean:...
of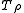 for the inner product induced by
for the inner product induced by  .
.
Finally the two operators are also connected, provided the images in question are defined, by the fundamental formula of composition:
Case of the Lebesgue measure and some other examples
The Lebesgue measure on the standard interval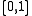 is obtained by taking the constant density
is obtained by taking the constant density 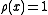 .
.
The associated orthogonal polynomialsOrthogonal polynomialsIn mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
are called Legendre polynomials and can be clarified by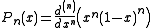 . The normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
. The normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of is worth
is worth  . The recurrence relation in three terms is written:
. The recurrence relation in three terms is written:
The reducer of this measure of Lebesgue is given by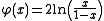 . The associated secondary measure is then clarified as :
. The associated secondary measure is then clarified as : 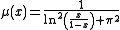 .
.
If we normalize the polynomials of Legendre, the coefficients of FourierFourierFourier most commonly refers to Joseph Fourier , French mathematician and physicist, or the mathematics, physics, and engineering terms named in his honor for his work on the concepts underlying them:In mathematics:...
of the reducer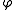 related to this orthonormal system are null for an even index and are given by
related to this orthonormal system are null for an even index and are given by 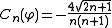 for an odd index
for an odd index  .
.
The Laguerre polynomialsLaguerre polynomialsIn mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
are linked to the density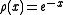 on the interval
on the interval  .
.
They are clarified by
and are normalized.
The reducer associated is defined by
The coefficients of Fourier of the reducer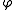 related to the Laguerre polynomials are given by
related to the Laguerre polynomials are given by
This coefficient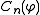 is no other than the opposite of the sum of the elements of the line of index
is no other than the opposite of the sum of the elements of the line of index  in the table of the harmonic triangular numbers of Leibniz.
in the table of the harmonic triangular numbers of Leibniz.
The Hermite polynomials are linked to the Gaussian density
-
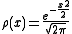 on
on 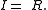
They are clarified by
and are normalized.
The reducer associated is defined by
The coefficients of FourierFourierFourier most commonly refers to Joseph Fourier , French mathematician and physicist, or the mathematics, physics, and engineering terms named in his honor for his work on the concepts underlying them:In mathematics:...
of the reducer related to the system of Hermite polynomials are null for an even index and are given by
related to the system of Hermite polynomials are null for an even index and are given by
for an odd index .
.
The Chebyshev measure of the second form. This is defined by the density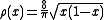 on the interval [0,1].
on the interval [0,1].
It is the only one which coincides with its secondary measure normalised on this standard interval. Under certain conditions it occurs as the limit of the sequence of normalized secondary measures of a given density.
Examples of non reducible measures.
JacobiJacobiJacobi may refer to:People with the surname Jacobi:*Jacobi Other:* Jacobi Medical Center, New York* Jacobi sum, a type of character sum in mathematics* Jacobi method, a method for diagonalization of matrices in mathematics...
measure of density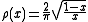 on (0, 1).
on (0, 1).
Chebyshev measure of the first form of density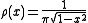 on (−1, 1).
on (−1, 1).
Sequence of secondary measures
The secondary measure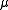 associated with a probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
associated with a probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
 has its moment of order 0 given by the formula
has its moment of order 0 given by the formula 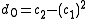 , (
, (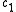 and
and 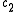 indicating the respective moments of order 1 and 2 of
indicating the respective moments of order 1 and 2 of 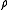 ).
).
To be able to iterate the process then, one 'normalizes'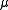 while defining
while defining 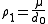 which becomes in its turn a density of probability called naturally the normalised secondary measure associated with
which becomes in its turn a density of probability called naturally the normalised secondary measure associated with 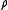 .
.
We can then create from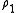 a secondary normalised measure
a secondary normalised measure 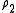 , then defining
, then defining 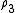 from
from 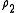 and so on. We can therefore see a sequence of successive secondary measures, created from
and so on. We can therefore see a sequence of successive secondary measures, created from 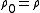 , is such that
, is such that 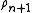 that is the secondary normalised measure deduced from
that is the secondary normalised measure deduced from 
It is possible to clarify the density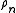 by using the orthogonal polynomialsOrthogonal polynomialsIn mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
by using the orthogonal polynomialsOrthogonal polynomialsIn mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
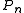 for
for  , the secondary polynomials
, the secondary polynomials 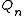 and the reducer associated
and the reducer associated 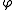 . That gives the formula
. That gives the formula
The coefficient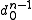 is easily obtained starting from the leading coefficients of the polynomials
is easily obtained starting from the leading coefficients of the polynomials 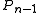 and
and 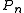 . We can also clarify the reducer
. We can also clarify the reducer 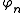 associated with
associated with 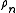 , as well as the orthogonal polynomials corresponding to
, as well as the orthogonal polynomials corresponding to 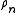 .
.
A very beautiful result relates the evolution of these densities when the index tends towards the infinite and the support of the measure is the standard interval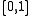 .
.
Let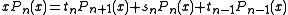 be the classic recurrence relation in three terms.
be the classic recurrence relation in three terms.
If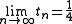 and
and  , then the sequence
, then the sequence  converges completely towards the Chebyshev density of the second form
converges completely towards the Chebyshev density of the second form 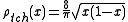 .
.
These conditions about limits are checked by a very broad class of traditional densities.
Equinormal measures
One calls two measures thus leading to the same normalised secondary density. It is remarkable that the elements of a given class and having the same moment of order 1 are connected by a homotopy. More precisely, if the density function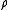 has its moment of order 1 equal to
has its moment of order 1 equal to 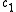 , then these densities equinormal with
, then these densities equinormal with 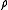 are given by a formula of the type:
are given by a formula of the type: 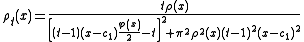 , t describing an interval containing]0, 1].
, t describing an interval containing]0, 1].
If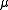 is the secondary measure of
is the secondary measure of  ,that of
,that of 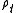 will be
will be 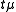 .
.
The reducer of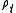 is :
is : 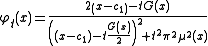 by noting
by noting 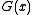 the reducer of
the reducer of 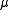 .
.
Orthogonal polynomials for the measure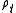 are clarified from
are clarified from  by the formula
by the formula
-
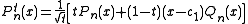 with
with 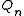 secondary polynomial associated with
secondary polynomial associated with 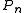
It is remarkable also that, within the meaning of distributions, the limit when tends towards 0 per higher value of
tends towards 0 per higher value of 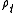 is the Dirac measure concentrated at
is the Dirac measure concentrated at 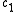 .
.
For example, the equinormal densities with the Chebyshev measure of the second form are defined by: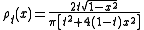 , with
, with  describing]0,2]. The value
describing]0,2]. The value  =2 gives the Chebyshev measure of the first form.
=2 gives the Chebyshev measure of the first form.
A few beautiful applications
-
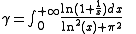 . (with
. (with  the Euler's constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
the Euler's constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
).
-
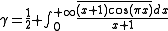 .
.
(the notation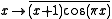 indicating the 2 periodic function coinciding with
indicating the 2 periodic function coinciding with 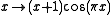 on (−1, 1)).
on (−1, 1)).
(with is the floor function and
is the floor function and 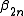 the Bernoulli numberBernoulli numberIn mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
the Bernoulli numberBernoulli numberIn mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
of order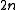 ).
).
(for any real )
)
(Ei indicate the integral exponentiel function here).
(The Catalan's constant is defined as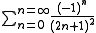 and
and  ) is the harmonic number of order
) is the harmonic number of order 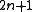 .
.
If the measure is reducible and let
is reducible and let  be the associated reducer, one has the equality
be the associated reducer, one has the equality
If the measure is reducible with
is reducible with 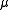 the associated reducer, then if
the associated reducer, then if 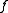 is square integrable for
is square integrable for 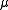 , and if
, and if 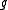 is square integrable for
is square integrable for 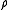 and is orthogonal with
and is orthogonal with 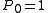 one has equivalence:
one has equivalence:
( indicates the moment of order 1 of
indicates the moment of order 1 of 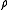 and
and 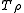 the operator
the operator 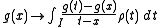 ).
).
External links
-
-
-
-
-