Secondary polynomials
Encyclopedia
In mathematics, the secondary polynomials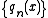 
associated with a sequence
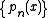of polynomials orthogonal
with respect to a density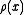
are defined by
To see that the functions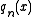
are indeed polynomials, consider the simple example of 
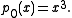Then,
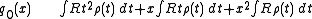
which is a polynomial
provided that the three integrals in 
(the moments
of the density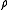
) are convergent.
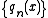associated with a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
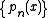of polynomials orthogonalOrthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
with respect to a density
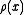are defined by
To see that the functions
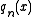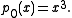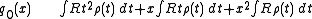
are indeed polynomials, consider the simple example of Then,which is a polynomial
provided that the three integrals in (the momentsMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of the density
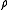) are convergent.