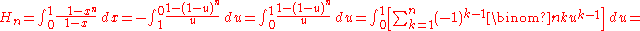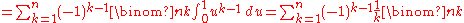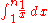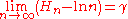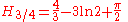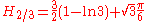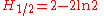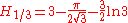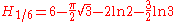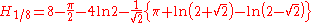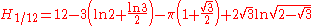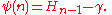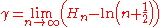
Harmonic number
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the n-th harmonic number is the sum of the reciprocals
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the first n natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s:
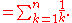
This also equals n times the inverse of the harmonic mean
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
of these natural numbers.
Harmonic numbers were studied in antiquity and are important in various branches of number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. They are sometimes loosely termed harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
, are closely related to the Riemann zeta function, and appear in various expressions for various special functions.
When the value of a large quantity of items has a Zipf's law distribution,
the total value of the n most-valuable items is the n-th harmonic number.
This leads to a variety of surprising conclusions in the Long Tail
The Long Tail
The Long Tail or long tail refers to the statistical property that a larger share of population rests within the tail of a probability distribution than observed under a 'normal' or Gaussian distribution...
and the theory of network value.
Calculation
An integral representation is given by Euler:
The equality above is obvious by the simple algebraic identity below
An elegant combinatorial expression can be obtained for
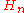using the simple integral transform 
:
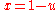The same representation can be produced by using the third Retkes identity putting
and using the fact that 
.
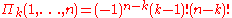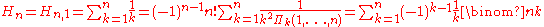
If we use Retkes identity for
in which case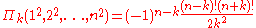 
one can have an analog formula for the n-th partial sum of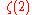 
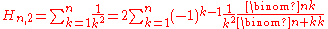
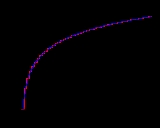
Hn grows about as fast as the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of n. The reason is that the sum is approximated by the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
whose value is ln(n).
The values of the sequence Hn - ln(n) decrease monotonically towards the limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
:
(where γ is the Euler–Mascheroni constant
Euler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
0.5772156649...), and the corresponding asymptotic expansion
Asymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
as
:
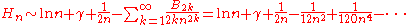
where
are the Bernoulli numbers.Special values for fractional arguments
There are the following special analytic values for fractional arguments between 0 and 1, given by the integral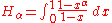
More may be generated from the recurrence relation
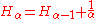or from the reflection relation 
.For every
, integer or not, we have: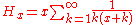 
Based on
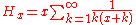, we have: 
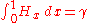, where 
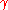is the Euler–Mascheroni constantEuler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
or, more generally, for every n we have:
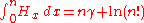
Generating functions
A generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the harmonic numbers is
where
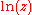is the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
. An exponential generating function is
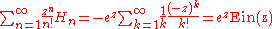
where
is the entire exponential integralExponential integral
In mathematics, the exponential integral is a special function defined on the complex plane given the symbol Ei.-Definitions:For real, nonzero values of x, the exponential integral Ei can be defined as...
. Note that
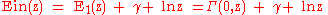
where
is the incomplete gamma functionIncomplete gamma function
In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
.
Applications
The harmonic numbers appear in several calculation formulas, such as the digamma function:
This relation is also frequently used to define the extension of the harmonic numbers to non-integer n. The harmonic numbers are also frequently used to define γ, using the limit introduced in the previous section, although
converges more quickly.
In 2002 Jeffrey Lagarias
Jeffrey Lagarias
Jeffrey Clark Lagarias is a mathematics professor at the University of Michigan.- Education :While in high school in 1966, Lagarias studied astronomy at the Summer Science Program....
proved that the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is equivalent to the statement that
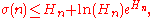
is true for every integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n ≥ 1 with strict inequality if n > 1; here σ(n) denotes the sum of the divisors
Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
of n.
Generalized harmonic numbers
The generalized harmonic number of order
of m is given by
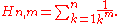
Note that the limit as n tends to infinity exists if
.Other notations occasionally used include
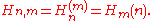
The special case of
is simply called a harmonic number and is frequently written without the superscript, as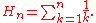
In the limit of
, the generalized harmonic number converges to the Riemann zeta function
The related sum
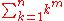occurs in the study of Bernoulli numberBernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s; the harmonic numbers also appear in the study of Stirling number
Stirling number
In mathematics, Stirling numbers arise in a variety of combinatorics problems. They are named after James Stirling, who introduced them in the 18th century. Two different sets of numbers bear this name: the Stirling numbers of the first kind and the Stirling numbers of the second...
s.
Some integrals of generalized harmonic are:
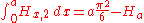
and
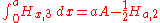where 
is the Apéry's constantApéry's constant
In mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics...
.
A generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the generalized harmonic numbers is
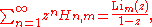
where
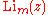is the polylogarithm, and |z| < 1. The generating function given above for m = 1 is a special case of this formula.Multiplication formulas
Using polygamma functions we obtains: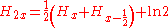
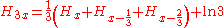
or, more generally:
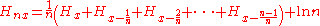
where
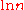is the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
.
For generalized harmonic numbers we have:
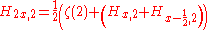
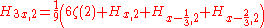
where
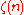is the Riemann zeta function.Generalization to the complex plane
Euler's integral formula for the harmonic numbers follows from the integral identity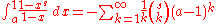
which holds for general complex-valued
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, for the suitably extended binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s. By choosing a=0, this formula gives both an integral and a series representation for a function that interpolates the harmonic numbers and extends a definition to the complex plane. This integral relation is easily derived by manipulating the Newton series
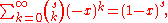
which is just the Newton's generalized binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
. The interpolating function is in fact the digamma function:
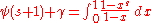
where
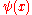is the digamma, and 
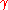is the Euler-Mascheroni constant. The integration process may be repeated to obtain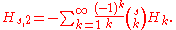
Relation to the Riemann zeta function
Some derivatives of fractional harmonic numbers are given by:
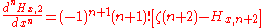
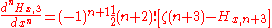
And using Maclaurin series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, we have for x<1 :
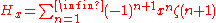
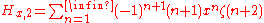
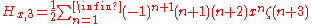
where
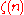is the Riemann zeta function.See also
- Watterson estimatorWatterson estimatorIn population genetics, the Watterson estimator is a method for estimating the population mutation rate, \theta = 4N_e\mu, where N_e is the effective population size and \mu is the per-generation mutation rate of the population of interest...
- Tajima's DTajima's DTajima's D is a statistical test created by and named after the Japanese researcher Fumio Tajima. The purpose of the test is to distinguish between a DNA sequence evolving randomly and one evolving under a non-random process, including directional selection or balancing selection, demographic...
- Coupon collector's problemCoupon collector's problemIn probability theory, the coupon collector's problem describes the "collect all coupons and win" contests. It asks the following question: Suppose that there are n coupons, from which coupons are being collected with replacement...
- Jeep problemJeep problemThe jeep problem, desert crossing problem or exploration problem is a mathematics problem in which a jeep must maximise the distance it can travel into a desert with a given quantity of fuel. The jeep can only carry a fixed and limited amount of fuel, but it can leave fuel and collect fuel at fuel...