
Residually finite group
Encyclopedia
In the mathematical
field of group theory
, a group
G is residually finite or finitely approximable if for every nontrivial element g in G there is a homomorphism
h from G to a finite group, such that

There are a number of equivalent definitions:
s, free group
s, finitely generated nilpotent group
s, polycyclic-by-finite groups, finitely generated linear groups
, and fundamental group
s of 3-manifold
s.
Subgroups of residually finite groups are residually finite, and direct products of residually finite groups are residually finite. Any inverse limit
of residually finite groups is residually finite. In particular, all profinite groups are residually finite.
by taking as a basis of open neighbourhoods of the identity, the collection of all normal subgroups of finite index in G. The resulting topology
is called the profinite topology on G. A group is residually finite if, and only if, its profinite topology is Hausdorff
.
A group whose cyclic subgroups are closed in the profinite topology is said to be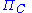 .
.
Groups, each of whose finitely generated subgroups are closed in the profinite topology are called subgroup separable (also LERF, for locally extended residually finite).
A group in which every conjugacy class
is closed in the profinite topology is called conjugacy separable.
all of whose groups are residually finite? Two results about these are:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is residually finite or finitely approximable if for every nontrivial element g in G there is a homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
h from G to a finite group, such that

There are a number of equivalent definitions:
- A group is residually finite if for each non-identity element in the group, there is a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of finite index not containing that element. - A group is residually finite if and only if the intersection of all its subgroups of finite index is trivial.
- A group is residually finite if and only if the intersection of all its normal subgroups of finite index is trivial.
- A group is residually finite if and only if it can be embedded inside the direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of a family of finite groups.
Examples
Examples of groups that are residually finite are finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s, finitely generated nilpotent group
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
s, polycyclic-by-finite groups, finitely generated linear groups
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
, and fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s.
Subgroups of residually finite groups are residually finite, and direct products of residually finite groups are residually finite. Any inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of residually finite groups is residually finite. In particular, all profinite groups are residually finite.
Profinite topology
Every group G may be made into a topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
by taking as a basis of open neighbourhoods of the identity, the collection of all normal subgroups of finite index in G. The resulting topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
is called the profinite topology on G. A group is residually finite if, and only if, its profinite topology is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
A group whose cyclic subgroups are closed in the profinite topology is said to be
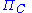 .
.Groups, each of whose finitely generated subgroups are closed in the profinite topology are called subgroup separable (also LERF, for locally extended residually finite).
A group in which every conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
is closed in the profinite topology is called conjugacy separable.
Varieties of residually finite groups
One question is: what are the properties of a varietyVariety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
all of whose groups are residually finite? Two results about these are:
- Any variety comprising only residually finite groups is generated by an A-groupA-groupA-Group is the designation for a distinct culture that arose between the First and Second Cataracts of the Nile in Nubia betweenthe Egyptian 1st dynasty and the 3rd millennium BC.The A-Group settled on very poor land with scarce natural resources, yet...
. - For any variety comprising only residually finite groups, it contains a finite group such that all members are embedded in a direct product of that finite group.

