Variety (universal algebra)
Encyclopedia
In mathematics
, specifically universal algebra
, a variety of algebras is the class
of all algebraic structure
s of a given signature
satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic
images, subalgebra
s and (direct) products
. In the context of category theory
, a variety of algebras is usually called a finitary algebraic category.
A covariety is the class
of all coalgebraic structures
of a given signature
.
A variety of algebras should not be confused with an algebraic variety
. Intuitively, a variety of algebras is an equationally defined collection of algebras, while an algebraic variety is an equationally defined collection of elements from a single algebra. The two are named alike by analogy, but they are formally quite distinct and their theories have little in common.
proved equivalent the two definitions of variety given above, a result of fundamental importance to universal algebra and known as Birkhoff's theorem or as the HSP theorem. H, S, and P stand, respectively, for the closure
operations
of homomorphism
, subalgebra
, and product
.
An equational class for some signature
Σ is the collection of all models, in the sense of model theory
, that satisfy some set E of equations, asserting equality between terms. A model satisfies these equations if they are true in the model for any valuation of the variables. The equations in E are then said to be identities of the model. Examples of such identities are the commutative law, characterizing commutative algebra
s, and the absorption law
, characterizing lattice
s.
It is simple to see that the class of algebras satisfying some set of equations will be closed under the HSP operations. Proving the converse —classes of algebras closed under the HSP operations must be equational— is much harder.
s forms a variety of algebras of signature (2). A sufficient defining equation is the associative law:
It satisfies the HSP closure requirement, since any homomorphic image, any subset closed under multiplication and any direct product of semigroups is also a semigroup.
The class of groups
forms a class of algebras of signature
(2,1,0), the three operations being respectively multiplication, inversion and identity.
Any subset of a group closed under multiplication, under inversion and under identity (i.e.
containing the identity) forms a subgroup. Likewise, the collection of groups is closed under homomorphic image and under direct product. Applying Birkhoff's theorem, this is sufficient to tell us that the groups form a variety, and so it should be defined by a collection of identities. In fact, the familiar axioms of associativity, inverse and identity form one suitable set of identities: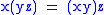
A subvariety of a variety V is a subclass of V that has the same signature as V and is itself a variety. Notice that although every group becomes a semigroup when the identity as a constant is omitted (and/or the inverse operation is omitted), the class of groups does not form a subvariety of the variety of semigroups because the signatures are different. On the other hand the class of abelian group
s is a subvariety of the variety of groups because it consists of those groups satisfying
with no change of signature. Viewing a variety V and its homomorphisms as a category
, a subclass U of V that is itself a variety is a subvariety of V implies that U is a full subcategory of V, meaning that for any objects a, b in U, the homomorphisms from a to b in U are exactly those from a to b in V. On the other hand there is a sense in which Boolean algebra
s and Boolean ring
s can be viewed as subvarieties of each other even though they have different signatures, because of the translation between them allowing every Boolean algebra to be understood as a Boolean ring and conversely; in this sort of situation the homomorphisms between corresponding structures are the same.
A variety of finite algebras, sometimes called a pseudovariety, is usually defined to be a class of finite algebras of a given signature, closed under the taking of homomorphic images, subalgebras and finitary direct products. There is no general finitary counterpart to
Birkhoff's theorem, but in many cases the introduction of a more complex notion of equations allows similar results to be derived.
Pseudovarieties are of particular importance in the study of finite semigroup
s and
hence in formal language theory
. Eilenberg's theorem, often referred to as the variety theorem describes a natural correspondence between varieties of regular language
s and pseudovarieties of finite semigroups.
is monadic
. Even more, it is strictly monadic, in that the comparison functor
is an isomorphism (and not just an equivalence). Here,
is the Eilenberg–Moore category on 
. In general, one says a category is an algebraic category if it is monadic over 
. This is a more general notion than "finitary algebraic category" (the notion of "variety" used in universal algebra) because it admits such categories as CABA (complete atomic Boolean algebras) and CSLat (complete semilattices) whose signatures include infinitary operations. In those two cases the signature is large, meaning that it forms not a set but a proper class, because its operations are of unbounded arity
. The algebraic category of sigma algebras also has infinitary operations, but their arity is countable whence its signature is small (forms a set).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, a variety of algebras is the class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of all algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s of a given signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
images, subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
s and (direct) products
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
. In the context of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a variety of algebras is usually called a finitary algebraic category.
A covariety is the class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of all coalgebraic structures
F-coalgebra
In mathematics, specifically in category theory, an F-coalgebra is a structure defined according to a functor F. For both algebra and coalgebra, a functor is a convenient and general way of organizing a signature...
of a given signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
.
A variety of algebras should not be confused with an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
. Intuitively, a variety of algebras is an equationally defined collection of algebras, while an algebraic variety is an equationally defined collection of elements from a single algebra. The two are named alike by analogy, but they are formally quite distinct and their theories have little in common.
Birkhoff's theorem
Garrett BirkhoffGarrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
proved equivalent the two definitions of variety given above, a result of fundamental importance to universal algebra and known as Birkhoff's theorem or as the HSP theorem. H, S, and P stand, respectively, for the closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
operations
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
of homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
, subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
, and product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
.
An equational class for some signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
Σ is the collection of all models, in the sense of model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, that satisfy some set E of equations, asserting equality between terms. A model satisfies these equations if they are true in the model for any valuation of the variables. The equations in E are then said to be identities of the model. Examples of such identities are the commutative law, characterizing commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
s, and the absorption law
Absorption law
In algebra, the absorption law or absorption identity is an identity linking a pair of binary operations.Two binary operations, say ¤ and *, are said to be connected by the absorption law if:...
, characterizing lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
s.
It is simple to see that the class of algebras satisfying some set of equations will be closed under the HSP operations. Proving the converse —classes of algebras closed under the HSP operations must be equational— is much harder.
Examples
The class of all semigroupSemigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s forms a variety of algebras of signature (2). A sufficient defining equation is the associative law:
It satisfies the HSP closure requirement, since any homomorphic image, any subset closed under multiplication and any direct product of semigroups is also a semigroup.
The class of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
forms a class of algebras of signature
(2,1,0), the three operations being respectively multiplication, inversion and identity.
Any subset of a group closed under multiplication, under inversion and under identity (i.e.
containing the identity) forms a subgroup. Likewise, the collection of groups is closed under homomorphic image and under direct product. Applying Birkhoff's theorem, this is sufficient to tell us that the groups form a variety, and so it should be defined by a collection of identities. In fact, the familiar axioms of associativity, inverse and identity form one suitable set of identities:
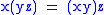
A subvariety of a variety V is a subclass of V that has the same signature as V and is itself a variety. Notice that although every group becomes a semigroup when the identity as a constant is omitted (and/or the inverse operation is omitted), the class of groups does not form a subvariety of the variety of semigroups because the signatures are different. On the other hand the class of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s is a subvariety of the variety of groups because it consists of those groups satisfying
with no change of signature. Viewing a variety V and its homomorphisms as a categoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a subclass U of V that is itself a variety is a subvariety of V implies that U is a full subcategory of V, meaning that for any objects a, b in U, the homomorphisms from a to b in U are exactly those from a to b in V. On the other hand there is a sense in which Boolean algebra
Boolean algebra
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets...
s and Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
s can be viewed as subvarieties of each other even though they have different signatures, because of the translation between them allowing every Boolean algebra to be understood as a Boolean ring and conversely; in this sort of situation the homomorphisms between corresponding structures are the same.
Variety of finite algebras
Since varieties are closed under arbitrary cartesian products, all non-trivial varieties contain infinite algebras. It follows that the theory of varieties is of limited use in the study of finite algebras, where one must often apply techniques particular to the finite case. With this in mind, attempts have been made to develop a finitary analogue of the theory of varieties.A variety of finite algebras, sometimes called a pseudovariety, is usually defined to be a class of finite algebras of a given signature, closed under the taking of homomorphic images, subalgebras and finitary direct products. There is no general finitary counterpart to
Birkhoff's theorem, but in many cases the introduction of a more complex notion of equations allows similar results to be derived.
Pseudovarieties are of particular importance in the study of finite semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s and
hence in formal language theory
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
. Eilenberg's theorem, often referred to as the variety theorem describes a natural correspondence between varieties of regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s and pseudovarieties of finite semigroups.
Category theory
If A is a finitary algebraic category, then the forgetful functorForgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
is monadic
Monad (category theory)
In category theory, a branch of mathematics, a monad, Kleisli triple, or triple is an functor, together with two natural transformations...
. Even more, it is strictly monadic, in that the comparison functor
is an isomorphism (and not just an equivalence). Here,
is the Eilenberg–Moore category on . In general, one says a category is an algebraic category if it is monadic over . This is a more general notion than "finitary algebraic category" (the notion of "variety" used in universal algebra) because it admits such categories as CABA (complete atomic Boolean algebras) and CSLat (complete semilattices) whose signatures include infinitary operations. In those two cases the signature is large, meaning that it forms not a set but a proper class, because its operations are of unbounded arityArity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
. The algebraic category of sigma algebras also has infinitary operations, but their arity is countable whence its signature is small (forms a set).