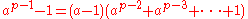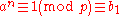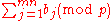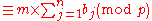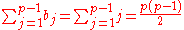
Proofs of Fermat's little theorem
Encyclopedia
This article collects together a variety of proofs
of Fermat's little theorem
, which states that
for every prime number
p and every integer
a (see modular arithmetic
).
The first is that we may assume that a is in the range 0 ≤ a ≤ p − 1. This is a simple consequence of the laws of modular arithmetic
; we are simply saying that we may first reduce a modulo p.
Secondly, it suffices to prove that
for a in the range 1 ≤ a ≤ p − 1. Indeed, if (X) holds for such a, then we can simply multiply both sides by a to obtain the original form of the theorem,
and if a happens to be zero, the original equation will not hold true, the final simplification is true for all 'a.'
(a proof that involves counting a collection of objects in two different ways
).
The proof given here is an adaptation of Golomb
's proof.
To keep things simple, let us assume that a is a positive integer. Consider all the possible string
s of p symbols, using an alphabet
with a different symbols. The total number of such strings is a p, since there are a possibilities for each of p positions (see rule of product
).
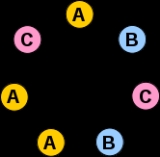
For example, if p = 5 and a = 2, then we can use an alphabet with two symbols (say A and B), and there are 25 = 32 strings of length five:
We will argue below that if we remove the strings consisting of a single symbol from the list (in our example, AAAAA and BBBBB), the remaining a p − a strings can be arranged into groups, each group containing exactly p strings. It follows that a p − a is divisible by p.
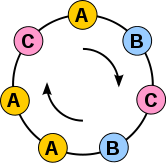
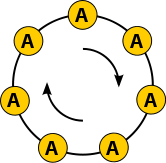 Let us think of each such string as representing a necklace
Let us think of each such string as representing a necklace
. That is, we connect the two ends of the string together, and regard two strings as the same necklace if we can rotate
one string to obtain the second string; in this case we will say that the two strings are friends. In our example, the following strings are all friends:
Similarly, each line of the following list corresponds to a single necklace.
Notice that in the above list, some necklaces are represented by five different strings, and some only by a single string, so the list shows very clearly why 32 − 2 is divisible by 5.
One can use the following rule to work out how many friends a given string S has:
For example, suppose we start with the string S = "ABBABBABBABB", which is built up of several copies of the shorter string T = "ABB". If we rotate it one symbol at a time, we obtain the following three strings:
There aren't any others, because ABB is exactly three symbols long, and cannot be broken down into further repeating strings.
The second category contains a p − a strings, and they may be arranged into groups of p strings, one group for each necklace. Therefore a p − a must be divisible by p, as promised.
Now
If ,
,  so a to any power is also congruent to 1 mod p, and the above equation is true for any p.
so a to any power is also congruent to 1 mod p, and the above equation is true for any p.
If and since
and since  , it suffices to prove that,
, it suffices to prove that,
Or
Since is a prime number,
is a prime number,  can be factorized. Let
can be factorized. Let  .
.
Let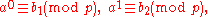 etc.
etc.
Then the terms of
terms of  can be tabulated as elements of an
can be tabulated as elements of an  matrix
matrix  :
:
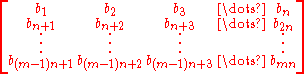
If :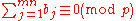
Then :
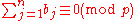
Then
Proof of Lemma 1:
If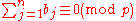
Then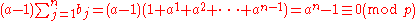
That is:
Thus the elements of second row of matrix are identical to those of the first row and hence the third and fourth rows etc. That is,
are identical to those of the first row and hence the third and fourth rows etc. That is,
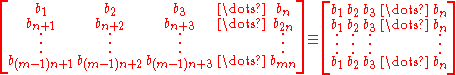
Thus
and hence

Then
Proof of Lemma 2:
If :
From Lemma 1,
Thus the elements of second row of matrix are not identical to that of the first row, neither are the third and fourth rows, etc. Conditions for Lemma 2 shall hold for all factor
are not identical to that of the first row, neither are the third and fourth rows, etc. Conditions for Lemma 2 shall hold for all factor 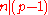 , any violation will result in satisfying the condition of Lemma 1 whereby the result has been proven. Consequently each value of
, any violation will result in satisfying the condition of Lemma 1 whereby the result has been proven. Consequently each value of 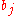 must be unique for
must be unique for  .
.
Since , the elements of matrix
, the elements of matrix  are no other than the set of numbers:
are no other than the set of numbers:

Thus
Hence
We have proven both lemmas and have completed the proof.
The integer is a divisor of . The smallest possible integer
is a divisor of . The smallest possible integer  is the Carmichael function, , which is .
is the Carmichael function, , which is .
The idea is that if we write down the sequence of numbers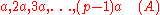
and reduce each one modulo p, the resulting sequence turns out to be a rearrangement of
Therefore, if we multiply together the numbers in each sequence, the results must be identical modulo p: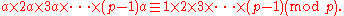
Collecting together the a terms yields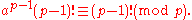
Finally, we may "cancel out" the numbers 1, 2, ..., p − 1 from both sides of this equation, obtaining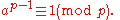
There are two steps in the above proof that we need to justify:
We will prove these things below; let us first see an example of this proof in action.
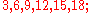
reducing modulo 7 gives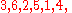
which is just a rearrangement of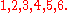
Multiplying them together gives
that is,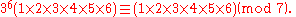
Canceling out 1 × 2 × 3 × 4 × 5 × 6 yields
which is Fermat's little theorem for the case a = 3 and p = 7.

when reduced modulo p, becomes a rearrangement of the sequence
To start with, none of the terms a, 2a, ..., (p − 1)a can be congruent to zero modulo p, since if k is one of the numbers 1, 2, ..., p − 1, then k is relatively prime with p, and so is a, so Euclid's lemma
tells us that ka shares no factor with p. Therefore, at least we know that the numbers a, 2a, ..., (p − 1)a, when reduced modulo p, must be found among the numbers 1, 2, 3, ..., p − 1. (also simply by the pigeonhole principle).
Furthermore, the numbers a, 2a, ..., (p − 1)a must all be distinct after reducing them modulo p, because if
where k and m are one of 1, 2, ..., p − 1, then the cancellation law tells us that
To summarise: when we reduce the p − 1 numbers a, 2a, ..., (p − 1)a modulo p, we obtain distinct members of the sequence 1, 2, ..., p − 1. Since there are exactly p − 1 of these, the only possibility is that the former are a rearrangement of the latter.

then we may "cancel" u to obtain
Our use of this cancellation law in the above proof of Fermat's little theorem was valid, because the numbers 1, 2, ..., p − 1 are certainly not divisible by p (indeed they are smaller than p).
We can prove the cancellation law easily using Euclid's lemma
, which generally states that if an integer b divides a product rs (where r and s are integers), and b is relatively prime to r, then b must divide s. Indeed, the equation
simply means that p divides ux − uy = u(x − y). Since p cannot divide u, since each factor of u is less than p and p is prime, therefore it cannot be the product of any factors of u, Euclid's lemma tells us that it must divide x − y instead; that is,
(Note that the conditions under which the cancellation law holds are quite strict, and this explains why Fermat's little theorem demands that p be a prime in order to make a general case for all n. For example, 2 × 2 ≡ 2 × 5 (mod 6), but we cannot conclude that 2 ≡ 5 (mod 6), since 6 is not prime. See below for a more extensive proof for all p)
For example:
Therefore,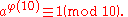
.
The idea is to recognise that the set G = {1, 2, …, p − 1}, with the operation of multiplication (taken modulo p), forms a group
. The only group axiom that requires some effort to verify is that each element of G is invertible. Taking this on trust for the moment, let us assume that a is in the range 1 ≤ a ≤ p − 1, that is, a is an element of G. Let k be the order
of a, so that
By Lagrange's theorem
, k divides the order of G, which is p − 1, so p − 1 = km for some positive integer m. Then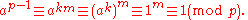
assures us that there are integers x and y such that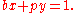
Reading this equation modulo p, we see that x is an inverse for b, since
Therefore every element of G is invertible, so as remarked earlier, G is a group.
For example, when p = 11, the inverses of each element are given as follows:
to prove the theorem for all integers a ≥ 0.
The base step, that 0 p ≡ 0 (mod p), is true for modular arithmetic because it is true for integers. Next, we must show that if the theorem is true for a = k, then it is also true for a = k+1. For this inductive step, we need the following lemma.
Lemma. For any prime p,
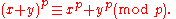
An alternative way of viewing this lemma is that it states that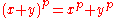
for any x and y in the finite field
GF(p).
Postponing the proof of the lemma for now, we proceed with the induction.
Proof. Assume kp ≡ k (mod p), and consider (k+1)p. By the lemma we have
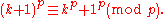
Using the induction hypothesis, we have that kp ≡ k (mod p); and, trivially, 1p = 1. Thus

which is the statement of the theorem for a = k+1. ∎
In order to prove the lemma, we must introduce the binomial theorem
, which states that for any positive integer n,
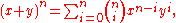
where the coefficients are the binomial coefficients,
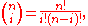
described in terms of the factorial
function, n! = 1×2×3×⋯×n.
Proof of lemma. The binomial coefficients are all integers and when 0 < i < p, neither of the terms in the denominator includes a factor of p, leaving the coefficient itself to possess a prime factor of p which must exist in the numerator, implying that
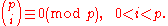
Modulo p, this eliminates all but the first and last terms of the sum on the left-hand side of the binomial theorem for prime p. ∎
The primality of p is essential to the lemma; otherwise, we have examples like
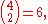
which is not divisible by 4.
s.
We start by considering a family of function
s, Tn(x), where n ≥ 2 is an integer
, mapping the interval
[0, 1] to itself by the formula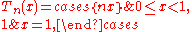
where {y} denotes the fractional part
of y. For example, the function T3(x) is illustrated below:
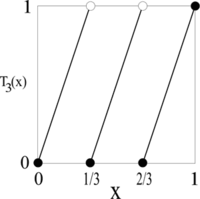 A number x0 is said to be a fixed point
A number x0 is said to be a fixed point
of a function f(x) if f(x0) = x0; in other words, if f leaves x0 fixed. The fixed points of a function can be easily found graphically: they are simply the x-coordinates of the points where the graph
of f(x) intersects the graph of the line y = x. For example, the fixed points of the function T3(x) are 0, 1/2, and 1; they are marked by black circles on the following diagram.
 We will require the following two lemmas.
We will require the following two lemmas.
Lemma 1. For any n ≥ 2, the function Tn(x) has exactly n fixed points.
Proof. There are three fixed points in the illustration above, and the same sort geometrical argument applies for any n ≥ 2.
Lemma 2. For any positive integers n and m, and any 0 ≤ x ≤ 1,
In other words, Tmn(x) is the composition
of Tn(x) and Tm(x).
Proof. The proof of this lemma is not difficult, but we need to be slightly careful with the endpoint x = 1. For this point the lemma is clearly true since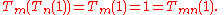
So let us assume that 0 ≤ x < 1. In this case,
so Tm(Tn(x)) is given by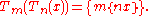
Therefore, what we really need to show is that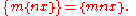
To do this we observe that {nx} = nx − k, where k is the integer part of nx; then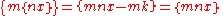
since mk is an integer.
Now let us properly begin the proof of Fermat's little theorem, by studying the function Ta p(x). We will assume that a is positive. From Lemma 1, we know that it has a p fixed points. By Lemma 2 we know that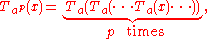
so any fixed point of Ta(x) is automatically a fixed point of Ta p(x).
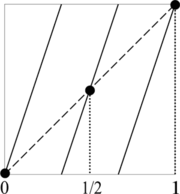
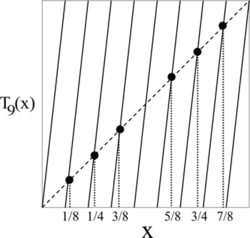
We are interested in the fixed points of Ta p(x) that are not fixed points of Ta(x). Let us call the set of such points S. There are a p − a points in S, because by Lemma 1 again, Ta(x) has exactly a fixed points. The following diagram illustrates the situation for a = 3 and p = 2. The black circles are the points of S, of which there are 32 − 3 = 6.
 The main idea of the proof is now to split the set S up into its orbits
The main idea of the proof is now to split the set S up into its orbits
under Ta. What this means is that we pick a point x0 in S, and repeatedly apply Ta(x) to it, to obtain the sequence of points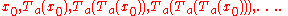
This sequence is called the orbit of x0 under Ta. By Lemma 2, this sequence can be rewritten as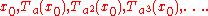
Since we are assuming that x0 is a fixed point of Ta p(x), after p steps we hit Ta p(x0) = x0, and from that point onwards the sequence repeats itself.
However, the sequence cannot begin repeating itself any earlier than that. If it did, the length of the repeating section would have to be a divisor of p, so it would have to be 1 (since p is prime). But this contradicts our assumption that x0 is not a fixed point of Ta.
In other words, the orbit contains exactly p distinct points. This holds for every orbit of S. Therefore, the set S, which contains a p − a points, can be broken up into orbits, each containing p points, so a p − a is divisible by p.
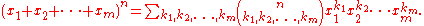
The summation is taken over all sequences of nonnegative integer indices k1 through km such the sum of all ki is n.
Thus if we express a as a sum of 1s (ones), we obtain
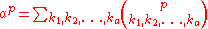
Clearly, if p is prime, and if kj not equal to p for any j, we have

and

if kj equal to p for some j
Since there are exactly a elements such that the theorem follows.
the theorem follows.
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
of Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
, which states that

for every prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p and every integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
a (see modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
).
Simplifications
Some of the proofs of Fermat's little theorem given below depend on two simplifications.The first is that we may assume that a is in the range 0 ≤ a ≤ p − 1. This is a simple consequence of the laws of modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
; we are simply saying that we may first reduce a modulo p.
Secondly, it suffices to prove that

for a in the range 1 ≤ a ≤ p − 1. Indeed, if (X) holds for such a, then we can simply multiply both sides by a to obtain the original form of the theorem,

and if a happens to be zero, the original equation will not hold true, the final simplification is true for all 'a.'
Proof by counting necklaces
This is perhaps the simplest known proof, requiring the least mathematical background. It is an attractive example of a combinatorial proofCombinatorial proof
In mathematics, the term combinatorial proof is often used to mean either of two types of proof of an identity in enumerative combinatorics that either states that two sets of combinatorial configurations, depending on one or more parameters, have the same number of elements , or gives a formula...
(a proof that involves counting a collection of objects in two different ways
Double counting (proof technique)
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
).
The proof given here is an adaptation of Golomb
Solomon W. Golomb
Solomon Wolf Golomb is an American mathematician and engineer and a professor of electrical engineering at the University of Southern California, best known to the general public and fans of mathematical games as the inventor of polyominoes, the inspiration for the computer game Tetris...
's proof.
To keep things simple, let us assume that a is a positive integer. Consider all the possible string
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
s of p symbols, using an alphabet
Alphabet
An alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
with a different symbols. The total number of such strings is a p, since there are a possibilities for each of p positions (see rule of product
Rule of product
In combinatorics, the rule of product or multiplication principle is a basic counting principle...
).
For example, if p = 5 and a = 2, then we can use an alphabet with two symbols (say A and B), and there are 25 = 32 strings of length five:
- AAAAA, AAAAB, AAABA, AAABB, AABAA, AABAB, AABBA, AABBB,
- ABAAA, ABAAB, ABABA, ABABB, ABBAA, ABBAB, ABBBA, ABBBB,
- BAAAA, BAAAB, BAABA, BAABB, BABAA, BABAB, BABBA, BABBB,
- BBAAA, BBAAB, BBABA, BBABB, BBBAA, BBBAB, BBBBA, BBBBB.
We will argue below that if we remove the strings consisting of a single symbol from the list (in our example, AAAAA and BBBBB), the remaining a p − a strings can be arranged into groups, each group containing exactly p strings. It follows that a p − a is divisible by p.
Necklaces


Necklace (combinatorics)
In combinatorics, a k-ary necklace of length n is an equivalence class of n-character strings over an alphabet of size k, taking all rotations as equivalent...
. That is, we connect the two ends of the string together, and regard two strings as the same necklace if we can rotate
Circular shift
In combinatorial mathematics, a circular shift is the operation of rearranging the entries in a tuple, either by moving the final entry to the first position, while shifting all other entries to the next position, or by performing the inverse operation...
one string to obtain the second string; in this case we will say that the two strings are friends. In our example, the following strings are all friends:
- AAAAB, AAABA, AABAA, ABAAA, BAAAA.
Similarly, each line of the following list corresponds to a single necklace.
- AAABB, AABBA, ABBAA, BBAAA, BAAAB,
- AABAB, ABABA, BABAA, ABAAB, BAABA,
- AABBB, ABBBA, BBBAA, BBAAB, BAABB,
- ABABB, BABBA, ABBAB, BBABA, BABAB,
- ABBBB, BBBBA, BBBAB, BBABB, BABBB,
- AAAAA,
- BBBBB.
Notice that in the above list, some necklaces are represented by five different strings, and some only by a single string, so the list shows very clearly why 32 − 2 is divisible by 5.
One can use the following rule to work out how many friends a given string S has:
- If S is built up of several copies of the string T, and T cannot itself be broken down further into repeating strings, then the number of friends of S (including S itself) is equal to the length of T.
For example, suppose we start with the string S = "ABBABBABBABB", which is built up of several copies of the shorter string T = "ABB". If we rotate it one symbol at a time, we obtain the following three strings:
- ABBABBABBABB,
- BBABBABBABBA,
- BABBABBABBAB.
There aren't any others, because ABB is exactly three symbols long, and cannot be broken down into further repeating strings.
Completing the proof
Using the above rule, we can complete the proof of Fermat's little theorem quite easily, as follows. Our starting pool of ap strings may be split into two categories:- Some strings contain p identical symbols. There are exactly a of these, one for each symbol in the alphabet. (In our running example, these are the strings AAAAA and BBBBB.)
- The rest of the strings use at least two distinct symbols from the alphabet. If we try to break up such a string S into repeating copies of a string T, we find that because p is prime, the only possibility is that T is already the whole string S. Therefore, the above rule tells us that S has exactly p friends (including S itself).
The second category contains a p − a strings, and they may be arranged into groups of p strings, one group for each necklace. Therefore a p − a must be divisible by p, as promised.
First method
To prove:Now
If
 ,
,  so a to any power is also congruent to 1 mod p, and the above equation is true for any p.
so a to any power is also congruent to 1 mod p, and the above equation is true for any p.If
 and since
and since  , it suffices to prove that,
, it suffices to prove that,Or
Since
 is a prime number,
is a prime number,  can be factorized. Let
can be factorized. Let  .
.Let
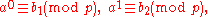 etc.
etc.Then the
 terms of
terms of  can be tabulated as elements of an
can be tabulated as elements of an  matrix
matrix  :
: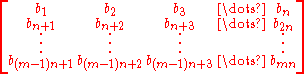
If :
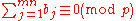
Then :

Lemma 1
If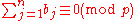
Then
Proof of Lemma 1:
If
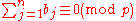
Then
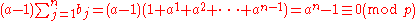
That is:
-
 etc.
etc.
Thus the elements of second row of matrix
 are identical to those of the first row and hence the third and fourth rows etc. That is,
are identical to those of the first row and hence the third and fourth rows etc. That is,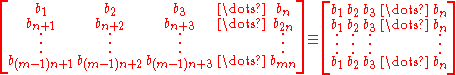
Thus
and hence
Lemma 2
If :
Then
Proof of Lemma 2:
If :

From Lemma 1,
Thus the elements of second row of matrix
 are not identical to that of the first row, neither are the third and fourth rows, etc. Conditions for Lemma 2 shall hold for all factor
are not identical to that of the first row, neither are the third and fourth rows, etc. Conditions for Lemma 2 shall hold for all factor 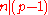 , any violation will result in satisfying the condition of Lemma 1 whereby the result has been proven. Consequently each value of
, any violation will result in satisfying the condition of Lemma 1 whereby the result has been proven. Consequently each value of 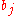 must be unique for
must be unique for  .
.Since
 , the elements of matrix
, the elements of matrix  are no other than the set of numbers:
are no other than the set of numbers:
Thus
Hence
We have proven both lemmas and have completed the proof.
Corollary
The proof also leads to the following corollary:- If
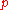 is a prime number, there exists an integer
is a prime number, there exists an integer  for every integer
for every integer  such that,
such that,
The integer
 is a divisor of . The smallest possible integer
is a divisor of . The smallest possible integer  is the Carmichael function, , which is .
is the Carmichael function, , which is .Second method
Let us assume that a is positive and not divisible by p.The idea is that if we write down the sequence of numbers
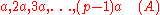
and reduce each one modulo p, the resulting sequence turns out to be a rearrangement of

Therefore, if we multiply together the numbers in each sequence, the results must be identical modulo p:
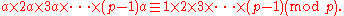
Collecting together the a terms yields
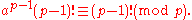
Finally, we may "cancel out" the numbers 1, 2, ..., p − 1 from both sides of this equation, obtaining
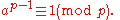
There are two steps in the above proof that we need to justify:
- Why (A) is a rearrangement of (B), and
- Why it is valid to "cancel" in the setting of modular arithmetic.
We will prove these things below; let us first see an example of this proof in action.
An example
If a = 3 and p = 7, then the sequence in question is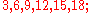
reducing modulo 7 gives
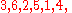
which is just a rearrangement of
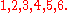
Multiplying them together gives

that is,
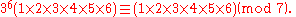
Canceling out 1 × 2 × 3 × 4 × 5 × 6 yields

which is Fermat's little theorem for the case a = 3 and p = 7.
The rearrangement property
Finally, we must explain why the sequence
when reduced modulo p, becomes a rearrangement of the sequence

To start with, none of the terms a, 2a, ..., (p − 1)a can be congruent to zero modulo p, since if k is one of the numbers 1, 2, ..., p − 1, then k is relatively prime with p, and so is a, so Euclid's lemma
Euclid's lemma
In mathematics, Euclid's lemma is an important lemma regarding divisibility and prime numbers. In its simplest form, the lemma states that a prime number that divides a product of two integers must divide one of the two integers...
tells us that ka shares no factor with p. Therefore, at least we know that the numbers a, 2a, ..., (p − 1)a, when reduced modulo p, must be found among the numbers 1, 2, 3, ..., p − 1. (also simply by the pigeonhole principle).
Furthermore, the numbers a, 2a, ..., (p − 1)a must all be distinct after reducing them modulo p, because if

where k and m are one of 1, 2, ..., p − 1, then the cancellation law tells us that

To summarise: when we reduce the p − 1 numbers a, 2a, ..., (p − 1)a modulo p, we obtain distinct members of the sequence 1, 2, ..., p − 1. Since there are exactly p − 1 of these, the only possibility is that the former are a rearrangement of the latter.
The cancellation law
Let us first explain why it is valid, in certain situations, to "cancel". The exact statement is as follows. If u, x, and y are integers, and u is not divisible by p, and if
then we may "cancel" u to obtain

Our use of this cancellation law in the above proof of Fermat's little theorem was valid, because the numbers 1, 2, ..., p − 1 are certainly not divisible by p (indeed they are smaller than p).
We can prove the cancellation law easily using Euclid's lemma
Euclid's lemma
In mathematics, Euclid's lemma is an important lemma regarding divisibility and prime numbers. In its simplest form, the lemma states that a prime number that divides a product of two integers must divide one of the two integers...
, which generally states that if an integer b divides a product rs (where r and s are integers), and b is relatively prime to r, then b must divide s. Indeed, the equation

simply means that p divides ux − uy = u(x − y). Since p cannot divide u, since each factor of u is less than p and p is prime, therefore it cannot be the product of any factors of u, Euclid's lemma tells us that it must divide x − y instead; that is,

(Note that the conditions under which the cancellation law holds are quite strict, and this explains why Fermat's little theorem demands that p be a prime in order to make a general case for all n. For example, 2 × 2 ≡ 2 × 5 (mod 6), but we cannot conclude that 2 ≡ 5 (mod 6), since 6 is not prime. See below for a more extensive proof for all p)
Applications to Euler's theorem
This method can also be used to prove Euler's theorem, with a slight alteration in that 1 to (p-1) is substituted for the numbers less than and relatively prime to some base m (instead of p). Both the rearrangement property and the cancellation law are still satisfied and can be utilized.For example:

Therefore,
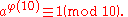
Proof using group theory
This proof requires the most basic elements of group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
.
The idea is to recognise that the set G = {1, 2, …, p − 1}, with the operation of multiplication (taken modulo p), forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. The only group axiom that requires some effort to verify is that each element of G is invertible. Taking this on trust for the moment, let us assume that a is in the range 1 ≤ a ≤ p − 1, that is, a is an element of G. Let k be the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of a, so that

By Lagrange's theorem
Lagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
, k divides the order of G, which is p − 1, so p − 1 = km for some positive integer m. Then
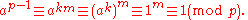
The invertibility property
To prove that every element b of G is invertible, we may proceed as follows. First, b is relatively prime to p. Then Bézout's identityBézout's identity
In number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
assures us that there are integers x and y such that
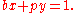
Reading this equation modulo p, we see that x is an inverse for b, since

Therefore every element of G is invertible, so as remarked earlier, G is a group.
For example, when p = 11, the inverses of each element are given as follows:
| a | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| a −1 | 1 | 6 | 4 | 3 | 9 | 2 | 8 | 7 | 5 | 10 |
Proof using the binomial theorem
This proof uses inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
to prove the theorem for all integers a ≥ 0.
The base step, that 0 p ≡ 0 (mod p), is true for modular arithmetic because it is true for integers. Next, we must show that if the theorem is true for a = k, then it is also true for a = k+1. For this inductive step, we need the following lemma.
Lemma. For any prime p,
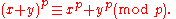
An alternative way of viewing this lemma is that it states that
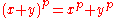
for any x and y in the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
GF(p).
Postponing the proof of the lemma for now, we proceed with the induction.
Proof. Assume kp ≡ k (mod p), and consider (k+1)p. By the lemma we have
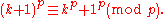
Using the induction hypothesis, we have that kp ≡ k (mod p); and, trivially, 1p = 1. Thus

which is the statement of the theorem for a = k+1. ∎
In order to prove the lemma, we must introduce the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
, which states that for any positive integer n,
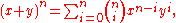
where the coefficients are the binomial coefficients,
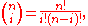
described in terms of the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
function, n! = 1×2×3×⋯×n.
Proof of lemma. The binomial coefficients are all integers and when 0 < i < p, neither of the terms in the denominator includes a factor of p, leaving the coefficient itself to possess a prime factor of p which must exist in the numerator, implying that
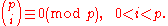
Modulo p, this eliminates all but the first and last terms of the sum on the left-hand side of the binomial theorem for prime p. ∎
The primality of p is essential to the lemma; otherwise, we have examples like
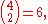
which is not divisible by 4.
Proof using dynamical systems
This proof uses some basic concepts from dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s.
We start by considering a family of function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s, Tn(x), where n ≥ 2 is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, mapping the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[0, 1] to itself by the formula
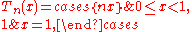
where {y} denotes the fractional part
Fractional part
All real numbers can be written in the form n + r where n is an integer and the remaining fractional part r is a nonnegative real number less than one...
of y. For example, the function T3(x) is illustrated below:

Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of a function f(x) if f(x0) = x0; in other words, if f leaves x0 fixed. The fixed points of a function can be easily found graphically: they are simply the x-coordinates of the points where the graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of f(x) intersects the graph of the line y = x. For example, the fixed points of the function T3(x) are 0, 1/2, and 1; they are marked by black circles on the following diagram.

Lemma 1. For any n ≥ 2, the function Tn(x) has exactly n fixed points.
Proof. There are three fixed points in the illustration above, and the same sort geometrical argument applies for any n ≥ 2.
Lemma 2. For any positive integers n and m, and any 0 ≤ x ≤ 1,

In other words, Tmn(x) is the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of Tn(x) and Tm(x).
Proof. The proof of this lemma is not difficult, but we need to be slightly careful with the endpoint x = 1. For this point the lemma is clearly true since
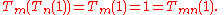
So let us assume that 0 ≤ x < 1. In this case,

so Tm(Tn(x)) is given by
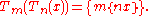
Therefore, what we really need to show is that
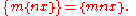
To do this we observe that {nx} = nx − k, where k is the integer part of nx; then
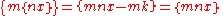
since mk is an integer.
Now let us properly begin the proof of Fermat's little theorem, by studying the function Ta p(x). We will assume that a is positive. From Lemma 1, we know that it has a p fixed points. By Lemma 2 we know that
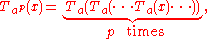
so any fixed point of Ta(x) is automatically a fixed point of Ta p(x).
We are interested in the fixed points of Ta p(x) that are not fixed points of Ta(x). Let us call the set of such points S. There are a p − a points in S, because by Lemma 1 again, Ta(x) has exactly a fixed points. The following diagram illustrates the situation for a = 3 and p = 2. The black circles are the points of S, of which there are 32 − 3 = 6.

Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
under Ta. What this means is that we pick a point x0 in S, and repeatedly apply Ta(x) to it, to obtain the sequence of points
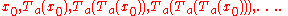
This sequence is called the orbit of x0 under Ta. By Lemma 2, this sequence can be rewritten as
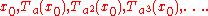
Since we are assuming that x0 is a fixed point of Ta p(x), after p steps we hit Ta p(x0) = x0, and from that point onwards the sequence repeats itself.
However, the sequence cannot begin repeating itself any earlier than that. If it did, the length of the repeating section would have to be a divisor of p, so it would have to be 1 (since p is prime). But this contradicts our assumption that x0 is not a fixed point of Ta.
In other words, the orbit contains exactly p distinct points. This holds for every orbit of S. Therefore, the set S, which contains a p − a points, can be broken up into orbits, each containing p points, so a p − a is divisible by p.
Proof using the Multinomial expansion
The proof is a very simple application of the Multinomial formula which is brought here for the sake of simplicity.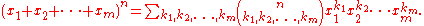
The summation is taken over all sequences of nonnegative integer indices k1 through km such the sum of all ki is n.
Thus if we express a as a sum of 1s (ones), we obtain
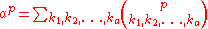
Clearly, if p is prime, and if kj not equal to p for any j, we have

and

if kj equal to p for some j
Since there are exactly a elements such that
 the theorem follows.
the theorem follows.