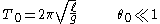.gif)
Pendulum (mathematics)
Encyclopedia
The mathematics of pendulum
s are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allows the equations of motion to be solved analytically for small-angle oscillations.
The differential equation
which represents the motion of a simple pendulum is
where g is acceleration due to gravity, l is the length of the pendulum, and θ is the angular displacement.
This is known as Mathieu
's equation.
,
then substituting for sin θ into (1) using the small-angle approximation,
,
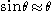yields the equation for a harmonic oscillator
The error due to the approximation is proportional to θ 3 (from the Maclaurin series for sin θ).
Given the initial conditions θ(0) = θ0 and dθ/dt(0) = 0, the solution becomes,
The motion is simple harmonic motion
where θ0 is the semi-amplitude of the oscillation (that is, the maximum angle between the rod of the pendulum and the vertical). The period of the motion, the time for a complete oscillation (outward and return) is
which is known as Christiaan Huygens's law for the period. Note that under the small-angle approximation, the period is independent of the amplitude θ0; this is the property of isochronism
that Galileo discovered.
can be expressed as 
If SI units
are used (i.e. measure in metres and seconds), and assuming the measurement is taking place on the Earth's surface, then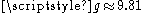
m/s2, and 
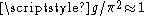(the exact figure is 0.994 to 3 decimal places).
Therefore a relatively reasonable approximation for the length and period are,
, one can compute the exact period by inverting equation (1)
and integrating over one complete cycle,
or twice the half-cycle
or 4 times the quarter-cycle
which leads to
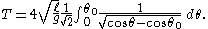
This integral can be re-written in the elliptic function of the first kind
(also see Jacobi's elliptic functions
), which gives little advantage since that form is also insoluble.
or more concisely, using the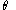
to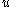 
substitution
,
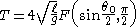
where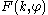
is Legendre's elliptic function of the first kind defined as
When
, 
is referred to as the complete elliptic function (or integral) of the first kind.
Figure 3 shows the deviation of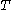
from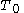 
, the period obtained from small-angle approximation.
Value for the complete elliptic function
can be computed using the rapidly convergent, highly accurate arithmetic-geometric mean method (see elliptic integrals), or alternatively computed using the following series:
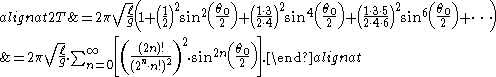
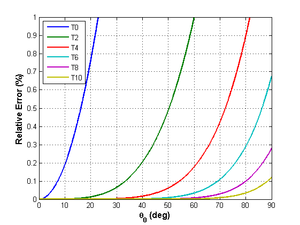
Figure 4 shows the relative errors using the power series. T0 is the linear approximation, and T2 to T10 include respectively the terms up to the 2nd to the 10th powers.
For a swing of exactly 180° the bob is balanced over its pivot point and so T = ∞.
For example, the period of a pendulum of length 1 m on Earth (g = 9.80665 m/s2) at initial angle 10 degrees is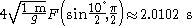 
, where the linear approximation gives 
.
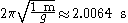The difference (less than 0.2%) is much less than that caused by the variation of g with geographical location.
By using the following Maclaurin series:
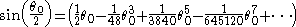
The equivalent power series is:
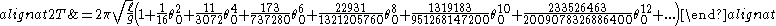
swinging by a pivot. In this case the pendulum's period depends on its moment of inertia
I around the pivot point.
The equation of torque
gives:
where:
is the angular acceleration.
is the torque
The torque is generated by gravity so:
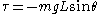
where:
Hence, under the small-angle approximation
,
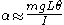
This is of the same form as the conventional simple pendulum and this gives a period of:
that expresses the position of a pendulum as a function of time is a doubly periodic function with a real
period and an imaginary
period. The real period is of course the time it takes the pendulum to go through one full cycle. Paul Appell pointed out a physical interpretation of the imaginary period: if θ0 is the maximum angle of one pendulum and 180° − θ0 is the maximum angle of another, then the real period of each is the magnitude of the imaginary period of the other.
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
s are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allows the equations of motion to be solved analytically for small-angle oscillations.
Simple gravity pendulum
A simple pendulum is an idealization of a real pendulum using the following assumptions:- The rod or cord on which the bob swings is massless, inextensible and always remains taut;
- Motion occurs only in two dimensions, i.e. the bob does not trace an ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
but an arcArc (geometry)In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...
. - The motion does not lose energy to frictionFrictionFriction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
or air resistance.
The differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
which represents the motion of a simple pendulum is
where g is acceleration due to gravity, l is the length of the pendulum, and θ is the angular displacement.
This is known as Mathieu
Émile Léonard Mathieu
Émile Léonard Mathieu was a French mathematician. He is most famous for his work in group theory and mathematical physics. He has given his name to the Mathieu functions, Mathieu groups and Mathieu transformation...
's equation.
Infinitesimal oscillations of a pendulum
The differential equation given above is not easily solved. However adding a restriction to the size of the oscillation's amplitude gives a form whose solution can be easily obtained. If it is assumed that the angle is much less than 1 radian, or,then substituting for sin θ into (1) using the small-angle approximation,
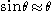,yields the equation for a harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
The error due to the approximation is proportional to θ 3 (from the Maclaurin series for sin θ).
Given the initial conditions θ(0) = θ0 and dθ/dt(0) = 0, the solution becomes,
The motion is simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
where θ0 is the semi-amplitude of the oscillation (that is, the maximum angle between the rod of the pendulum and the vertical). The period of the motion, the time for a complete oscillation (outward and return) is
which is known as Christiaan Huygens's law for the period. Note that under the small-angle approximation, the period is independent of the amplitude θ0; this is the property of isochronism
Isochronous
Isochronous : From Greek iso, equal + chronos, time. It literally means regularly, or at equal time intervals. In general English language, it refers to something that occurs at a regular interval, of the same duration; as opposed to synchronous which refers to more than one thing happening at the...
that Galileo discovered.
Rule of thumb for pendulum length
can be expressed as If SI units
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
are used (i.e. measure in metres and seconds), and assuming the measurement is taking place on the Earth's surface, then
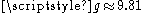m/s2, and 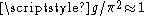(the exact figure is 0.994 to 3 decimal places).Therefore a relatively reasonable approximation for the length and period are,
Arbitrary-amplitude period
For amplitudes beyond the small angle approximationSmall angle approximation
The small-angle approximation is a useful simplification of the basic trigonometric functions which is approximately true in the limit where the angle approaches zero. They are truncations of the Taylor series for the basic trigonometric functions to a second-order approximation...
, one can compute the exact period by inverting equation (1)
and integrating over one complete cycle,
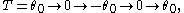
or twice the half-cycle
or 4 times the quarter-cycle
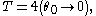
which leads to
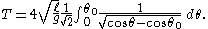
This integral can be re-written in the elliptic function of the first kind
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
(also see Jacobi's elliptic functions
Jacobi's elliptic functions
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that have historical importance with also many features that show up important structure, and have direct relevance to some applications...
), which gives little advantage since that form is also insoluble.
or more concisely, using the
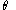to 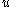substitutionIntegration by substitution
In calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
,
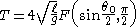
where
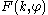is Legendre's elliptic function of the first kind defined as
When
, is referred to as the complete elliptic function (or integral) of the first kind.Figure 3 shows the deviation of
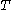from 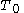, the period obtained from small-angle approximation.Value for the complete elliptic function
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
can be computed using the rapidly convergent, highly accurate arithmetic-geometric mean method (see elliptic integrals), or alternatively computed using the following series:
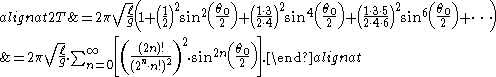
Figure 4 shows the relative errors using the power series. T0 is the linear approximation, and T2 to T10 include respectively the terms up to the 2nd to the 10th powers.
For a swing of exactly 180° the bob is balanced over its pivot point and so T = ∞.
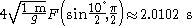, where the linear approximation gives 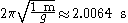.The difference (less than 0.2%) is much less than that caused by the variation of g with geographical location.
By using the following Maclaurin series:
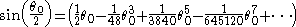
The equivalent power series is:
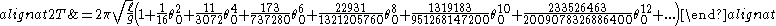
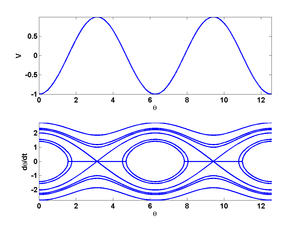
Examples
The animations below depict several different modes of oscillation given different initial conditions. The small graph above the pendulums are their phase portraits.Compound pendulum
A compound pendulum is one where the rod is not massless, and may have extended size; that is, an arbitrarily shaped rigid bodyRigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
swinging by a pivot. In this case the pendulum's period depends on its moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
I around the pivot point.
The equation of torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
gives:
where:
is the angular acceleration. is the torqueThe torque is generated by gravity so:
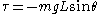
where:
- L is the distance from the pivot to the center of mass of the pendulum
- θ is the angle from the vertical
Hence, under the small-angle approximation
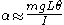
,This is of the same form as the conventional simple pendulum and this gives a period of:
Physical interpretation of the imaginary period
The Jacobian elliptic functionJacobi's elliptic functions
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that have historical importance with also many features that show up important structure, and have direct relevance to some applications...
that expresses the position of a pendulum as a function of time is a doubly periodic function with a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
period and an imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
period. The real period is of course the time it takes the pendulum to go through one full cycle. Paul Appell pointed out a physical interpretation of the imaginary period: if θ0 is the maximum angle of one pendulum and 180° − θ0 is the maximum angle of another, then the real period of each is the magnitude of the imaginary period of the other.
See also
- Blackburn pendulumBlackburn pendulumA Blackburn pendulum, named after Hugh Blackburn, is a device for illustrating harmonic motion. A bob is suspended from a string that in turn hangs from a V-shaped pair of strings, so that the pendulum oscillates simultaneously in two perpendicular directions with different periods. The bob...
- Conical pendulumConical pendulumA conical pendulum is a weight fixed on the end of a string suspended from a pivot. Its construction is similar to an ordinary pendulum; however, instead of rocking back and forth, the bob of a conical pendulum moves at a constant speed in a circle with the string tracing out a cone...
- Double pendulumDouble pendulumIn mathematics, in the area of dynamical systems, a double pendulum is a pendulum with another pendulum attached to its end, and is a simple physical system that exhibits rich dynamic behavior with a strong sensitivity to initial conditions. The motion of a double pendulum is governed by a set of...
- Inverted pendulumInverted pendulumAn inverted pendulum is a pendulum which has its mass above its pivot point. It is often implemented with the pivot point mounted on a cart that can move horizontally and may be called a cart and pole...
- Spring pendulumSpring pendulumA spring pendulum is a physical system where a mass is connected to a spring so that the resulting motion contains elements of a simple pendulum as well as a spring. The system is much more complex than a simple pendulum because the properties of the spring adds an extra dimension of freedom to...
- Mathieu functionMathieu functionIn mathematics, the Mathieu functions are certain special functions useful for treating a variety of problems in applied mathematics, including*vibrating elliptical drumheads,*quadrupoles mass filters and quadrupole ion traps for mass spectrometry...
- Pendulum equations (software)
Further reading
- The Pendulum: A Physics Case Study, Gregory L. Baker and James A. Blackburn, Oxford University Press, 2005
- Kenneth L. Sala, “Transformations of the Jacobian Amplitude Function and its Calculation via the Arithmetic-Geometric Mean”, SIAM J. Math. Anal., vol. 20, no. 6, pp. 1514–1528, Nov. 1989.
- Karlheinz Ochs, “A comprehensive analytical solution of the nonlinear pendulum”, European Journal of Physics, vol. 32, no. 2, pp. 479–490, 2011.