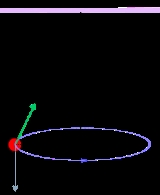
Conical pendulum
Encyclopedia
A conical pendulum is a weight (or bob
) fixed on the end of a string (or rod) suspended from a pivot. Its construction is similar to an ordinary pendulum
; however, instead of rocking back and forth, the bob of a conical pendulum moves at a constant speed in a circle
with the string (or rod) tracing out a cone
. The conical pendulum was first studied by the English scientist Robert Hooke
around 1660 as a model for the orbital motion of planet
s. In 1673 Dutch scientist Christiaan Huygens calculated its period, using his new concept of centrifugal force
. Later it was used as the timekeeping element in a few mechanical clocks and other clockwork timing devices.
s to sweep their beams across the sea, and the tracking drives of equatorial mount
telescope
s, to allow the telescope to follow a star smoothly across the sky as the Earth turns. They were also used in some bedroom clocks, to avoid the ticking sound of a pendulum or balance wheel
movement
, which could disturb sleep.
Conical pendulums had other uses unrelated to timekeeping. A pair of conical pendulums served as key components in the centrifugal governor
s used to regulate the operational speed of steam engines.
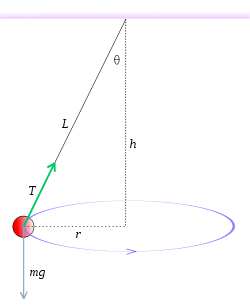
of mass m revolving without friction in a circle at a constant speed v on a string of length L at an angle of θ from the vertical.
There are two forces acting on the bob:
The force exerted by the string can be resolved into a horizontal component, T sin(θ), toward the center of the circle, and a vertical component, T cos(θ), in the upward direction. From Newton's second law, the horizontal component of the tension in the string gives the bob a centripetal acceleration toward the center of the circle:

 Since there is no acceleration in the vertical direction, the vertical component of the tension in the string is equal and opposite to the weight of the bob:
Since there is no acceleration in the vertical direction, the vertical component of the tension in the string is equal and opposite to the weight of the bob:
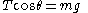
These two equations can be solved for T/m and equated, thereby eliminating T and m:
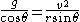
Since the speed of the pendulum bob is constant, it can be expressed as the circumference 2πr divided by the time t required for one revolution of the bob:
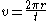
Substituting the right side of this equation for v in the previous equation, we find:

Using the trigonometric identity tan(θ) = sin(θ) / cos(θ) and solving for t, the time required for the bob to travel one revolution is
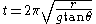
In a practical experiment, r varies and is not as easy to measure as the constant string length L. r can be eliminated from the equation by noting that r, h, and L form a right triangle, with θ being the angle between the leg h and the hypotenuse L (see diagram). Therefore,
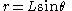
Substituting this value for r yields a formula whose only varying parameter is the suspension angle θ:

For small angles θ, cos(θ) ≈ 1, and the period t of a conical pendulum is equal to the period of an ordinary pendulum of the same length. Also, the period for small angles is approximately independent of changes in the angle θ. This means the period of rotation is approximately independent of the force applied to keep it rotating. This property, called isochronism
, is shared with ordinary pendulums and makes both types of pendulums useful for timekeeping.
Bob (physics)
A bob is the weight on the end of a pendulum most commonly, but not exclusively, found in pendulum clocks.- Reason for use :Although a pendulum can theoretically be any shape, any rigid object swinging on a pivot, clock pendulums are usually made of a weight or bob attached to the bottom end of a...
) fixed on the end of a string (or rod) suspended from a pivot. Its construction is similar to an ordinary pendulum
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
; however, instead of rocking back and forth, the bob of a conical pendulum moves at a constant speed in a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
with the string (or rod) tracing out a cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
. The conical pendulum was first studied by the English scientist Robert Hooke
Robert Hooke
Robert Hooke FRS was an English natural philosopher, architect and polymath.His adult life comprised three distinct periods: as a scientific inquirer lacking money; achieving great wealth and standing through his reputation for hard work and scrupulous honesty following the great fire of 1666, but...
around 1660 as a model for the orbital motion of planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s. In 1673 Dutch scientist Christiaan Huygens calculated its period, using his new concept of centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
. Later it was used as the timekeeping element in a few mechanical clocks and other clockwork timing devices.
Uses
During the 1800s, conical pendulums were used as the timekeeping element in a few clockwork timing mechanisms where a smooth motion was required, as opposed to the unavoidably jerky motion provided by ordinary pendulums. Two examples were mechanisms to turn the lenses of lighthouseLighthouse
A lighthouse is a tower, building, or other type of structure designed to emit light from a system of lamps and lenses or, in older times, from a fire, and used as an aid to navigation for maritime pilots at sea or on inland waterways....
s to sweep their beams across the sea, and the tracking drives of equatorial mount
Equatorial mount
An equatorial mount is a mount for instruments that follows the rotation of the sky by having one rotational axis parallel to the Earth's axis of rotation. This type of mount is used for astronomical telescopes and cameras...
telescope
Telescope
A telescope is an instrument that aids in the observation of remote objects by collecting electromagnetic radiation . The first known practical telescopes were invented in the Netherlands at the beginning of the 1600s , using glass lenses...
s, to allow the telescope to follow a star smoothly across the sky as the Earth turns. They were also used in some bedroom clocks, to avoid the ticking sound of a pendulum or balance wheel
Balance wheel
The balance wheel is the timekeeping device used in mechanical watches and some clocks, analogous to the pendulum in a pendulum clock. It is a weighted wheel that rotates back and forth, being returned toward its center position by a spiral spring, the balance spring or hairspring...
movement
Movement (clockwork)
In horology, a movement is the internal mechanism of a clock or watch, as opposed to the case, which encloses and protects the movement, and the face which displays the time. The term originated with mechanical timepieces, whose movements are made of many moving parts...
, which could disturb sleep.
Conical pendulums had other uses unrelated to timekeeping. A pair of conical pendulums served as key components in the centrifugal governor
Centrifugal governor
A centrifugal governor is a specific type of governor that controls the speed of an engine by regulating the amount of fuel admitted, so as to maintain a near constant speed whatever the load or fuel supply conditions...
s used to regulate the operational speed of steam engines.
Analysis
Consider a conical pendulum consisting of a bobBob (physics)
A bob is the weight on the end of a pendulum most commonly, but not exclusively, found in pendulum clocks.- Reason for use :Although a pendulum can theoretically be any shape, any rigid object swinging on a pivot, clock pendulums are usually made of a weight or bob attached to the bottom end of a...
of mass m revolving without friction in a circle at a constant speed v on a string of length L at an angle of θ from the vertical.
There are two forces acting on the bob:
- the tension T in the string, which is exerted along the line of the string and acts toward the point of suspension.
- the downward bob weightWeightIn science and engineering, the weight of an object is the force on the object due to gravity. Its magnitude , often denoted by an italic letter W, is the product of the mass m of the object and the magnitude of the local gravitational acceleration g; thus:...
mg, where m is the massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the bob and g is the local gravitational accelerationGravitational accelerationIn physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
.
The force exerted by the string can be resolved into a horizontal component, T sin(θ), toward the center of the circle, and a vertical component, T cos(θ), in the upward direction. From Newton's second law, the horizontal component of the tension in the string gives the bob a centripetal acceleration toward the center of the circle:


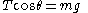
These two equations can be solved for T/m and equated, thereby eliminating T and m:
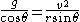
Since the speed of the pendulum bob is constant, it can be expressed as the circumference 2πr divided by the time t required for one revolution of the bob:
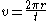
Substituting the right side of this equation for v in the previous equation, we find:

Using the trigonometric identity tan(θ) = sin(θ) / cos(θ) and solving for t, the time required for the bob to travel one revolution is
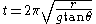
In a practical experiment, r varies and is not as easy to measure as the constant string length L. r can be eliminated from the equation by noting that r, h, and L form a right triangle, with θ being the angle between the leg h and the hypotenuse L (see diagram). Therefore,
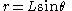
Substituting this value for r yields a formula whose only varying parameter is the suspension angle θ:

For small angles θ, cos(θ) ≈ 1, and the period t of a conical pendulum is equal to the period of an ordinary pendulum of the same length. Also, the period for small angles is approximately independent of changes in the angle θ. This means the period of rotation is approximately independent of the force applied to keep it rotating. This property, called isochronism
Isochronous
Isochronous : From Greek iso, equal + chronos, time. It literally means regularly, or at equal time intervals. In general English language, it refers to something that occurs at a regular interval, of the same duration; as opposed to synchronous which refers to more than one thing happening at the...
, is shared with ordinary pendulums and makes both types of pendulums useful for timekeeping.
See also
- Newton's three laws of motion
- PendulumPendulumA pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
- Pendulum (mathematics)Pendulum (mathematics)The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allows the equations of motion to be solved analytically for small-angle oscillations.- Simple gravity pendulum :...

