
Inverted pendulum
Encyclopedia
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
which has its mass above its pivot point. It is often implemented with the pivot point mounted on a cart that can move horizontally and may be called a cart and pole. Whereas a normal pendulum is stable when hanging downwards, an inverted pendulum is inherently unstable, and must be actively balanced in order to remain upright, either by applying a torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
at the pivot point or by moving the pivot point horizontally as part of a feedback
Feedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
system. A simple demonstration is achieved by balancing an upturned broomstick on the end of one's finger.
Overview
The inverted pendulum is a classic problem in dynamicsDynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
and control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
and is widely used as a benchmark for testing control algorithms (PID controller
PID controller
A proportional–integral–derivative controller is a generic control loop feedback mechanism widely used in industrial control systems – a PID is the most commonly used feedback controller. A PID controller calculates an "error" value as the difference between a measured process variable and a...
s, neural networks
Neural Networks
Neural Networks is the official journal of the three oldest societies dedicated to research in neural networks: International Neural Network Society, European Neural Network Society and Japanese Neural Network Society, published by Elsevier...
, fuzzy control, genetic algorithm
Genetic algorithm
A genetic algorithm is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems...
s, etc.). Variations on this problem include multiple links, allowing the motion of the cart to be commanded while maintaining the pendulum, and balancing the cart-pendulum system on a see-saw. The inverted pendulum is related to rocket or missile guidance, where the center of gravity is located behind the center of drag causing aerodynamic instability. The understanding of a similar problem can be shown by simple robotics in the form of a balancing cart. Balancing an upturned broomstick on the end of one's finger is a simple demonstration, and the problem is solved in the technology of the Segway PT
Segway PT
The Segway PT is a two-wheeled, self-balancing transportation machine invented by Dean Kamen. It is produced by Segway Inc. of New Hampshire, USA. The name "Segway" is a homophone of "segue" while "PT" denotes personal transporter....
, a self-balancing transportation device.
Another way that an inverted pendulum may be stabilized, without any feedback or control mechanism, is by oscillating the support rapidly up and down. If the oscillation is sufficiently strong (in terms of its acceleration and amplitude) then the inverted pendulum can recover from perturbations in a strikingly counterintuitive manner. If the driving point moves in simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
, the pendulum's motion is described by the Mathieu equation.
Stationary pivot point
The equation of motion is similar to that for an uninverted pendulumPendulum (mathematics)
The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allows the equations of motion to be solved analytically for small-angle oscillations.- Simple gravity pendulum :...
except that the sign of the angular position as measured from the vertical unstable
Instability
In numerous fields of study, the component of instability within a system is generally characterized by some of the outputs or internal states growing without bounds...
equilibrium
Mechanical equilibrium
A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
position:

When added to both sides, it will have the same sign as the angular acceleration
Angular acceleration
Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :...
term:
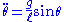
Thus, the inverted pendulum will accelerate away from the vertical unstable equilibrium in the direction initially displaced, and the acceleration is inversely proportional to the length. Tall pendulums fall more slowly than short ones.
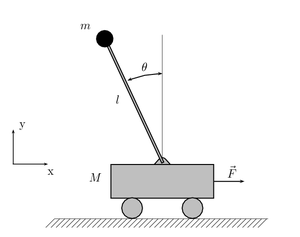
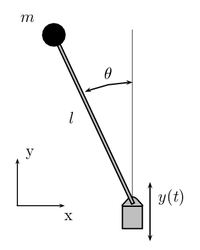
Pendulum on a cart
The equations of motion can be derived using Lagrange's equationsLagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
. We refer to the drawing above where
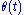 is the angle of the pendulum of length
is the angle of the pendulum of length 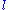 with respect to the vertical direction and the acting forces are gravity and an external force F in the x-direction. Define
with respect to the vertical direction and the acting forces are gravity and an external force F in the x-direction. Define 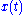 to be the position of the cart. The Lagrangian
to be the position of the cart. The LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
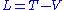 of the system is:
of the system is: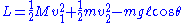
where
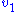 is the velocity of the cart and
is the velocity of the cart and 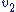 is the velocity of the point mass
is the velocity of the point mass  .
.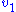 and
and 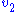 can be expressed in terms of x and
can be expressed in terms of x and 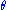 by writing the velocity as the first derivative of the position;
by writing the velocity as the first derivative of the position;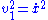
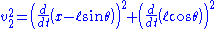
Simplifying the expression for
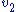 leads to:
leads to: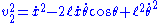
The Lagrangian is now given by:
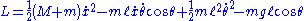
and the equations of motion are:
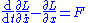
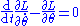
substituting
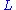 in these equations and simplifying leads to the equations that describe the motion of the inverted pendulum:
in these equations and simplifying leads to the equations that describe the motion of the inverted pendulum:
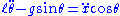
These equations are nonlinear, but since the goal of a control system would be to keep the pendulum upright the equations can be linearized around
 .
.Pendulum with oscillatory base
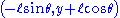
and the velocity is found by taking the first derivative of the position:
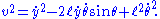
The Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
for this system can be written as:
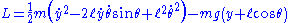
and the equation of motion follows from:
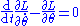
resulting in:
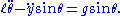
If y represents a simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
,
 , the following differential equation
, the following differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
is:
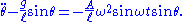
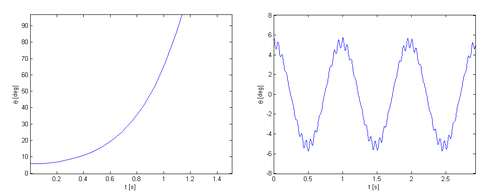
 is a slow oscillation, the pendulum quickly falls over when disturbed from the upright position. The angle
is a slow oscillation, the pendulum quickly falls over when disturbed from the upright position. The angle  exceeds 90° after a short time, which means the pendulum has fallen on the ground.
exceeds 90° after a short time, which means the pendulum has fallen on the ground.If
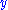 is a fast oscillation the pendulum can be kept stable around the vertical position. The second plot shows that when disturbed from the vertical position, the pendulum now starts an oscillation around the vertical position (
is a fast oscillation the pendulum can be kept stable around the vertical position. The second plot shows that when disturbed from the vertical position, the pendulum now starts an oscillation around the vertical position ( ). The deviation from the vertical position stays small, and the pendulum doesn't fall over.
). The deviation from the vertical position stays small, and the pendulum doesn't fall over.Applications
The inverted pendulum was a central component in the design of several earlySeismometer
Seismometer
Seismometers are instruments that measure motions of the ground, including those of seismic waves generated by earthquakes, volcanic eruptions, and other seismic sources...
s.
See also
- Self-balancing unicycle
- Segway PTSegway PTThe Segway PT is a two-wheeled, self-balancing transportation machine invented by Dean Kamen. It is produced by Segway Inc. of New Hampshire, USA. The name "Segway" is a homophone of "segue" while "PT" denotes personal transporter....
- Double inverted pendulumDouble inverted pendulumA double inverted pendulum is combination of the inverted pendulum and the double pendulum. The double inverted pendulum is unstable, meaning that it will fall down unless it is controlled in some way...
- Inertia wheel pendulumInertia wheel pendulumAn inertia wheel pendulum or gyroscopic pendulum is a pendulum with an inertia wheel attached. It can be used as a pedagogical problem in control theory.- References :* Mark W. Spong, Peter Corke, Rogelio Lozano. ....
- Furuta pendulumFuruta pendulumThe Furuta pendulum, or rotational inverted pendulum, consists of a driven arm which rotates in the horizontal plane and a pendulum attached to that arm which is free to rotate in the vertical plane .- Overview :...
Further reading
- Franklin; et al. (2005). Feedback control of dynamic systems, 5, Prentice Hall. ISBN 0-13-149930-0

