
Multiplicative partition
Encyclopedia
In number theory
, a multiplicative partition or unordered factorization of an integer n that is greater than 1 is a way of writing n as a product of integers greater than 1, treating two products as equivalent if they differ only in the ordering of the factors. The number n is itself considered one of these products. Multiplicative partitions closely parallel the study of multipartite partitions, discussed in , which are additive partitions
of finite sequences of positive integers, with the addition made pointwise
. Although the study of multiplicative partitions has been ongoing since at least 1923, the name "multiplicative partition" appears to have been introduced by . The Latin name "factorisatio numerorum" had been used previously. MathWorld
uses the name unordered factorization.
s; these forms correspond to the multiplicative partitions 12, 2×6, 3×4, and 2×2×3 respectively. More generally, for each multiplicative partition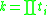
of the integer k, there corresponds a class of integers having exactly k divisors, of the form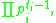
where each pi is a distinct prime. This correspondence follows from the multiplicative
property of the divisor function
.
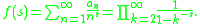
The sequence of numbers an begins
Oppenheim also claimed an upper bound on an, of the form
but as showed, this bound is erroneous and the true bound is

Both of these bounds are not far from linear in n: they are of the form n1−o(1).
However, the typical value of an is much smaller: the average value of an, averaged over an interval x ≤ n ≤ x+N, is
a bound that is of the form no(1) .
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a multiplicative partition or unordered factorization of an integer n that is greater than 1 is a way of writing n as a product of integers greater than 1, treating two products as equivalent if they differ only in the ordering of the factors. The number n is itself considered one of these products. Multiplicative partitions closely parallel the study of multipartite partitions, discussed in , which are additive partitions
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of finite sequences of positive integers, with the addition made pointwise
Pointwise
In mathematics, the qualifier pointwise is used to indicate that a certain property is defined by considering each value f of some function f. An important class of pointwise concepts are the pointwise operations — operations defined on functions by applying the operations to function values...
. Although the study of multiplicative partitions has been ongoing since at least 1923, the name "multiplicative partition" appears to have been introduced by . The Latin name "factorisatio numerorum" had been used previously. MathWorld
MathWorld
MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
uses the name unordered factorization.
Examples
- The number 20 has four multiplicative partitions: 2 × 2 × 5, 2 × 10, 4 × 5, and 20.
- 3 × 3 × 3 × 3, 3 × 3 × 9, 3 × 27, 9 × 9, and 81 are the five multiplicative permutations of 81 = 34. Because it is the fourth power of a primePrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, 81 has the same number (five) of multiplicative partitions as 4 does of additive partitionsPartition (number theory)In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
. - The number 30 has five multiplicative partitions: 2 × 3 × 5 = 2 × 15 = 6 × 5 = 3 × 10 = 30.
- In general, the number of multiplicative partitions of a squarefreeSquare-free integerIn mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
number with i prime factors is the ith Bell numberBell numberIn combinatorics, the nth Bell number, named after Eric Temple Bell, is the number of partitions of a set with n members, or equivalently, the number of equivalence relations on it...
, Bi.
Application
describe an application of multiplicative partitions in classifying integers with a given number of divisors. For example, the integers with exactly 12 divisors take the forms p11, p×q5, p2×q3, and p×q×r2, where p, q, and r are distinct prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s; these forms correspond to the multiplicative partitions 12, 2×6, 3×4, and 2×2×3 respectively. More generally, for each multiplicative partition
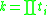
of the integer k, there corresponds a class of integers having exactly k divisors, of the form
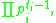
where each pi is a distinct prime. This correspondence follows from the multiplicative
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
property of the divisor function
Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
.
Bounds on the number of partitions
credits with the problem of counting the number of multiplicative partitions of n; this problem has since been studied by other others under the Latin name of factorisatio numerorum. If the number of multiplicative partitions of n is an, McMahon and Oppenheim observed that its Dirichlet series generating function ƒ(s) has the product representation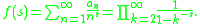
The sequence of numbers an begins
- 1, 1, 1, 2, 1, 2, 1, 3, 2, 2, 1, 4, 1, 2, 2, 5, ... .
Oppenheim also claimed an upper bound on an, of the form

but as showed, this bound is erroneous and the true bound is

Both of these bounds are not far from linear in n: they are of the form n1−o(1).
However, the typical value of an is much smaller: the average value of an, averaged over an interval x ≤ n ≤ x+N, is

a bound that is of the form no(1) .

