Isoclinism of groups
Encyclopedia
In mathematics, specifically group theory
, isoclinism is an equivalence relation
on groups
that is broader than isomorphism
, that is, any two groups that are isomorphic are isoclinic, but two isoclinic groups may not be isomorphic. The concept of isoclinism was introduced by to help classify and understand p-group
s, although applicable to all groups. Isoclinism remains an important part of the study of p-groups, and for instance §29 of and §21.2 of are devoted to it. Isoclinism also has vital consequences for the Schur multiplier
and the associated aspects of character theory
, as described in and .
s are isoclinic since they are equal to their centers and their commutator subgroups are always the identity subgroup. Indeed, a group is isoclinic to an abelian group if and only if it is itself abelian, and G is isoclinic with G×A if and only if A is abelian. The dihedral
, quasidihedral
, and quaternion group
s of order 2n are isoclinic for n≥3, .
Isoclinism divides p-groups into families, and the smallest members of each family are called stem groups. A group is a stem group if and only if Z(G) ≤ [G,G], that is, if and only if every element of the center of the group is contained in the derived subgroup (also called the commutator subgroup), . Some enumeration results on isoclinism families are given in .
Another textbook treatment of isoclinism is given in , which describes in more detail the isomorphisms induced by an isoclinism. Isoclinism is important in theory of projective representation
s of finite group
s, as all Schur covering groups of a group are isoclinic, a fact already hinted at by Hall according to . This is important in describing the character tables of the finite simple groups, and so is described in some detail in .
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, isoclinism is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
that is broader than isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, that is, any two groups that are isomorphic are isoclinic, but two isoclinic groups may not be isomorphic. The concept of isoclinism was introduced by to help classify and understand p-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
s, although applicable to all groups. Isoclinism remains an important part of the study of p-groups, and for instance §29 of and §21.2 of are devoted to it. Isoclinism also has vital consequences for the Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
and the associated aspects of character theory
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
, as described in and .
Definition
According to , two groups G and G' are isoclinic if the following three conditions hold:-
is isomorphic to 
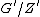, where 
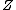is the centerCenter (group theory)In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of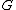
and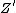 
is the center of 
. - The commutator subgroupCommutator subgroupIn mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of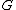
is isomorphic to the commutator subgroup of 
. - "The isomorphisms of (1) and (2) can be selected in such a way that whenever
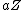and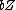 
correspond respectively to 
and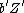 
under (1), then 
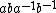corresponds to 
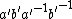under (2)."
Examples
All Abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s are isoclinic since they are equal to their centers and their commutator subgroups are always the identity subgroup. Indeed, a group is isoclinic to an abelian group if and only if it is itself abelian, and G is isoclinic with G×A if and only if A is abelian. The dihedral
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
, quasidihedral
Quasidihedral group
In mathematics, the quasi-dihedral groups and semi-dihedral groups are non-abelian groups of order a power of 2. For every positive integer n greater than or equal to 4, there are exactly four isomorphism classes of nonabelian groups of order 2n which have a cyclic subgroup of index 2...
, and quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
s of order 2n are isoclinic for n≥3, .
Isoclinism divides p-groups into families, and the smallest members of each family are called stem groups. A group is a stem group if and only if Z(G) ≤ [G,G], that is, if and only if every element of the center of the group is contained in the derived subgroup (also called the commutator subgroup), . Some enumeration results on isoclinism families are given in .
Another textbook treatment of isoclinism is given in , which describes in more detail the isomorphisms induced by an isoclinism. Isoclinism is important in theory of projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, as all Schur covering groups of a group are isoclinic, a fact already hinted at by Hall according to . This is important in describing the character tables of the finite simple groups, and so is described in some detail in .