
Ohm's law
Encyclopedia
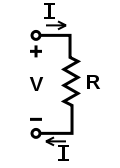
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
through a conductor between two points is directly proportional
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the potential difference across the two points. Introducing the constant of proportionality, the resistance
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
, one arrives at the usual mathematical equation that describes this relationship:
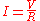
where I is the current through the conductor in units of ampere
Ampere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
s, V is the potential difference measured across the conductor in units of volt
Volt
The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the...
s, and R is the resistance
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
of the conductor in units of ohm
Ohm
The ohm is the SI unit of electrical resistance, named after German physicist Georg Simon Ohm.- Definition :The ohm is defined as a resistance between two points of a conductor when a constant potential difference of 1 volt, applied to these points, produces in the conductor a current of 1 ampere,...
s. More specifically, Ohm's law states that the R in this relation is constant, independent of the current.
The law was named after the German physicist Georg Ohm
Georg Ohm
Georg Simon Ohm was a German physicist. As a high school teacher, Ohm began his research with the recently-invented electrochemical cell, invented by Italian Count Alessandro Volta. Using equipment of his own creation, Ohm determined that there is a direct proportionality between the potential...
, who, in a treatise published in 1827, described measurements of applied voltage and current through simple electrical circuits containing various lengths of wire. He presented a slightly more complex equation than the one above (see History section below) to explain his experimental results. The above equation is the modern form of Ohm's law.
In physics, the term Ohm's law is also used to refer to various generalizations of the law originally formulated by Ohm. The simplest example of this is:

where J is the current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
at a given location in a resistive material, E is the electric field at that location, and σ is a material dependent parameter called the conductivity. This reformulation of Ohm's law is due to Gustav Kirchhoff
Gustav Kirchhoff
Gustav Robert Kirchhoff was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black-body radiation by heated objects...
.
Microscopic origins of Ohm's law
The dependence of the current density on the applied electric field is essentially quantum mechanicalQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
in nature; (see Classical and quantum conductivity
Classical and quantum conductivity
Classical and quantum mechanical views of conductivity have both described the movements of electrons in a metallic solid. The free electron gas that is present in metallic solids is the reason for an important property of all metals: conductivity...
.) A qualitative description leading to Ohm's law can be based upon classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
using the Drude model
Drude model
The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials...
developed by Paul Drude in 1900.
The Drude model treats electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s (or other charge carriers) like pinballs bouncing between the ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s that make up the structure of the material. Electrons will be accelerated in the opposite direction to the electric field by the average electric field at their location. With each collision, though, the electron is deflected in a random direction with a velocity that is much larger than the velocity gained by the electric field. The net result is that electrons take a tortuous path due to the collisions, but generally drift in a direction opposing the electric field.
The drift velocity
Drift velocity
The drift velocity is the average velocity that a particle, such as an electron, attains due to an electric field. It can also be referred to as Axial Drift Velocity since particles defined are assumed to be moving along a plane. In general, an electron will 'rattle around' in a conductor at the...
then determines the electric current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
and its relationship to E and is independent of the collisions. Drude calculated the average drift velocity from p = −eEτ where p is the average momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, −e is the charge of the electron and τ is the average time between the collisions. Since both the momentum and the current density are proportional to the drift velocity, the current density becomes proportional to the applied electric field; this leads to Ohm's law.
Hydraulic analogy
A hydraulic analogyHydraulic analogy
The electronic–hydraulic analogy is the most widely used analogy for "electron fluid" in a metal conductor. Since electric current is invisible and the processes at play in electronics are often difficult to demonstrate, the various electronic components are represented by hydraulic...
is sometimes used to describe Ohm's Law. Water pressure, measured by pascals
Pascal (unit)
The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...
(or PSI
Pounds per square inch
The pound per square inch or, more accurately, pound-force per square inch is a unit of pressure or of stress based on avoirdupois units...
), is the analog of voltage because establishing a water pressure difference between two points along a (horizontal) pipe causes water to flow. Water flow rate, as in liter
Litér
- External links :*...
s per second, is the analog of current, as in coulombs per second. Finally, flow restrictors—such as apertures placed in pipes between points where the water pressure is measured—are the analog of resistors. We say that the rate of water flow through an aperture restrictor is proportional to the difference in water pressure across the restrictor. Similarly, the rate of flow of electrical charge, that is, the electric current, through an electrical resistor is proportional to the difference in voltage measured across the resistor.
Flow and pressure variables can be calculated in fluid flow network with the use of the hydraulic ohm analogy. The method can be applied to both steady and transient flow situations. In the linear laminar flow
Laminar flow
Laminar flow, sometimes known as streamline flow, occurs when a fluid flows in parallel layers, with no disruption between the layers. At low velocities the fluid tends to flow without lateral mixing, and adjacent layers slide past one another like playing cards. There are no cross currents...
region, Poiseuille's law describes the hydraulic resistance of a pipe, but in the turbulent flow region the pressure–flow relations become nonlinear.
The hydraulic analogy to Ohm's law has been used, for example, to approximate blood flow through the circulatory system.
Circuit analysis
In circuit analysis, three equivalent expressions of Ohm's law are used interchangeably: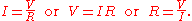
Each equation is quoted by some sources as the defining relationship of Ohm's law,
or all three are quoted, or derived from a proportional form,
or even just the two that do not correspond to Ohm's original statement may sometimes be given.
The interchangeability of the equation may be represented by a triangle, where V (voltage
Voltage
Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
) is placed on the top section, the I (current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
) is placed to the left section, and the R (resistance
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
) is placed to the right. The line that divides the left and right sections indicate multiplication, and the divider between the top and bottom sections indicates division (hence the division bar).
Resistive circuits
ResistorResistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
s are circuit elements that impede the passage of electric charge in agreement with Ohm's law, and are designed to have a specific resistance value R. In a schematic diagram the resistor is shown as a zig-zag symbol. An element (resistor or conductor) that behaves according to Ohm's law over some operating range is referred to as an ohmic device (or an ohmic resistor) because Ohm's law and a single value for the resistance suffice to describe the behavior of the device over that range.
Ohm's law holds for circuits containing only resistive elements (no capacitances or inductances) for all forms of driving voltage or current, regardless of whether the driving voltage or current is constant (DC
Direct current
Direct current is the unidirectional flow of electric charge. Direct current is produced by such sources as batteries, thermocouples, solar cells, and commutator-type electric machines of the dynamo type. Direct current may flow in a conductor such as a wire, but can also flow through...
) or time-varying such as AC
Alternating current
In alternating current the movement of electric charge periodically reverses direction. In direct current , the flow of electric charge is only in one direction....
. At any instant of time Ohm's law is valid for such circuits.
Resistors which are in series or in parallel may be grouped together into a single "equivalent resistance" in order to apply Ohm's law in analyzing the circuit. This application of Ohm's law is illustrated with examples in "How To Analyze Resistive Circuits Using Ohm's Law" on wikiHow
WikiHow
wikiHow is a web-based and wiki-based community, consisting of an extensive database of how-to guides. wikiHow's mission is to build the world's largest and highest quality how-to manual. The site started as an extension of the already existing eHow website, and has evolved to host over 127,000...
.
Reactive circuits with time-varying signals
When reactive elements such as capacitors, inductors, or transmission lines are involved in a circuit to which AC or time-varying voltage or current is applied, the relationship between voltage and current becomes the solution to a differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
, so Ohm's law (as defined above) does not directly apply since that form contains only resistances having value R, not complex impedances which may contain capacitance ("C") or inductance ("L").
Equations for time-invariant AC
Alternating current
In alternating current the movement of electric charge periodically reverses direction. In direct current , the flow of electric charge is only in one direction....
circuits take the same form as Ohm's law, however, the variables are generalized to complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s and the current and voltage waveforms are complex exponentials.
In this approach, a voltage or current waveform takes the form
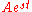 , where t is time, s is a complex parameter, and A is a complex scalar. In any linear time-invariant system
, where t is time, s is a complex parameter, and A is a complex scalar. In any linear time-invariant systemLTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
, all of the currents and voltages can be expressed with the same s parameter as the input to the system, allowing the time-varying complex exponential term to be canceled out and the system described algebraically in terms of the complex scalars in the current and voltage waveforms.
The complex generalization of resistance is impedance
Electrical impedance
Electrical impedance, or simply impedance, is the measure of the opposition that an electrical circuit presents to the passage of a current when a voltage is applied. In quantitative terms, it is the complex ratio of the voltage to the current in an alternating current circuit...
, usually denoted Z; it can be shown that for an inductor,
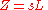
and for a capacitor,
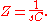
We can now write,

where V and I are the complex scalars in the voltage and current respectively and Z is the complex impedance.
This form of Ohm's law, with Z taking the place of R, generalizes the simpler form. When Z is complex, only the real part is responsible for dissipating heat.
In the general AC circuit, Z varies strongly with the frequency parameter s, and so also will the relationship between voltage and current.
For the common case of a steady sinusoid, the s parameter is taken to be
 , corresponding to a complex sinusoid
, corresponding to a complex sinusoid  . The real parts of such complex current and voltage waveforms describe the actual sinusoidal currents and voltages in a circuit, which can be in different phases due to the different complex scalars.
. The real parts of such complex current and voltage waveforms describe the actual sinusoidal currents and voltages in a circuit, which can be in different phases due to the different complex scalars.Linear approximations
Ohm's law is one of the basic equations used in the analysis of electrical circuitsNetwork analysis (electrical circuits)
A network, in the context of electronics, is a collection of interconnected components. Network analysis is the process of finding the voltages across, and the currents through, every component in the network. There are a number of different techniques for achieving this...
. It applies to both metal conductors and circuit components (resistor
Resistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
s) specifically made for this behaviour. Both are ubiquitous in electrical engineering. Materials and components that obey Ohm's law are described as "ohmic" which means they produce the same value for resistance (R = V/I) regardless of the value of V or I which is applied and whether the applied voltage or current is DC (direct current
Direct current
Direct current is the unidirectional flow of electric charge. Direct current is produced by such sources as batteries, thermocouples, solar cells, and commutator-type electric machines of the dynamo type. Direct current may flow in a conductor such as a wire, but can also flow through...
) of either positive or negative polarity or AC (alternating current
Alternating current
In alternating current the movement of electric charge periodically reverses direction. In direct current , the flow of electric charge is only in one direction....
).
In a true ohmic device, the same value of resistance will be calculated from R = V/I regardless of the value of the applied voltage V. That is, the ratio of V/I is constant, and when current is plotted as a function of voltage the curve is linear (a straight line). If voltage is forced to some value V, then that voltage V divided by measured current I will equal R. Or if the current is forced to some value I, then the measured voltage V divided by that current I is also R. Since the plot of I versus V is a straight line, then it is also true that for any set of two different voltages V1 and V2 applied across a given device of resistance R, producing currents I1 = V1/R and I2 = V2/R, that the ratio (V1-V2)/(I1-I2) is also a constant equal to R. The operator "delta" (Δ) is used to represent a difference in a quantity, so we can write ΔV = V1-V2 and ΔI = I1-I2. Summarizing, for any truly ohmic device having resistance R, V/I = ΔV/ΔI = R for any applied voltage or current or for the difference between any set of applied voltages or currents.
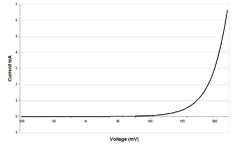
Direct current
Direct current is the unidirectional flow of electric charge. Direct current is produced by such sources as batteries, thermocouples, solar cells, and commutator-type electric machines of the dynamo type. Direct current may flow in a conductor such as a wire, but can also flow through...
, resistance, but as seen in the figure the value of total V over total I varies depending on the particular point along the nonlinear curve which is chosen. This means the "DC resistance" V/I at some point on the curve is not the same as what would be determined by applying an AC signal having peak amplitude ΔV volts or ΔI amps centered at that same point along the curve and measuring ΔV/ΔI. However, in some diode applications, the AC signal applied to the device is small and it is possible to analyze the circuit in terms of the dynamic, small-signal, or incremental resistance, defined as the one over the slope of the V–I curve at the average value (DC operating point) of the voltage (that is, one over the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of current with respect to voltage). For sufficiently small signals, the dynamic resistance allows the Ohm's law small signal resistance to be calculated as approximately one over the slope of a line drawn tangentially to the V-I curve at the DC operating point.
Temperature effects
Ohm's law has sometimes been stated as, "for a conductor in a given state, the electromotive force is proportional to the current produced." That is, that the resistance, the ratio of the applied electromotive forceElectromotive force
In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
(or voltage) to the current, "does not vary with the current strength ." The qualifier "in a given state" is usually interpreted as meaning "at a constant temperature," since the resistivity of materials is usually temperature dependent. Because the conduction of current is related to Joule heating
Joule heating
Joule heating, also known as ohmic heating and resistive heating, is the process by which the passage of an electric current through a conductor releases heat. It was first studied by James Prescott Joule in 1841. Joule immersed a length of wire in a fixed mass of water and measured the temperature...
of the conducting body, according to Joule's first law, the temperature of a conducting body may change when it carries a current. The dependence of resistance on temperature therefore makes resistance depend upon the current in a typical experimental setup, making the law in this form difficult to directly verify. Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
and others worked out several methods to test the law experimentally in 1876, controlling for heating effects.
Relation to heat conductions
Ohm's principle predicts the flow of electrical charge (i.e. current) in electrical conductors when subjected to the influence of voltage differences; Jean-Baptiste-Joseph Fourier's principle predicts the flow of heatHeat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
in heat conductors when subjected to the influence of temperature differences.
The same equation describes both phenomena, the equation's variables taking on different meanings in the two cases. Specifically, solving a heat conduction (Fourier) problem with temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
(the driving "force") and flux of heat
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
(the rate of flow of the driven "quantity", i.e. heat energy) variables also solves an analogous electrical conduction (Ohm) problem having electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
(the driving "force") and electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
(the rate of flow of the driven "quantity", i.e. charge) variables.
The basis of Fourier's work was his clear conception and definition of thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
. He assumed that, all else being the same, the flux of heat is strictly proportional to the gradient of temperature. Although undoubtedly true for small temperature gradients, strictly proportional behavior will be lost when real materials (e.g. ones having a thermal conductivity that is a function of temperature) are subjected to large temperature gradients.
A similar assumption is made in the statement of Ohm's law: other things being alike, the strength of the current at each point is proportional to the gradient of electric potential. The accuracy of the assumption that flow is proportional to the gradient is more readily tested, using modern measurement methods, for the electrical case than for the heat case.
Other versions of Ohm's law
Ohm's law, in the form above, is an extremely useful equation in the field of electrical/electronic engineering because it describes how voltage, current and resistance are interrelated on a "macroscopic" level, that is, commonly, as circuit elements in an electrical circuit. Physicists who study the electrical properties of matter at the microscopic level use a closely related and more general vectorVector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
equation, sometimes also referred to as Ohm's law, having variables that are closely related to the V, I, and R scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
variables of Ohm's law, but which are each functions of position within the conductor. Physicists often use this continuum form of Ohm's Law:
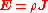
where "E" is the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
vector with units of volts per meter (analogous to "V" of Ohm's law which has units of volts), "J" is the current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
vector with units of amperes per unit area (analogous to "I" of Ohm's law which has units of amperes), and "ρ" (Greek "rho") is the resistivity
Resistivity
Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre...
with units of ohm·meters (analogous to "R" of Ohm's law which has units of ohms). The above equation is sometimes written as J =
 E where "σ" is the conductivity which is the reciprocal of ρ.
E where "σ" is the conductivity which is the reciprocal of ρ.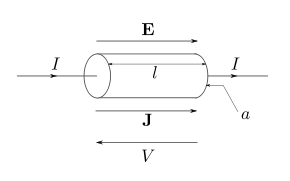
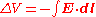
with
 the element of path along the integration of electric field vector E. If the applied E field is uniform and oriented along the length of the conductor as shown in the figure, then defining the voltage V in the usual convention of being opposite in direction to the field (see figure), and with the understanding that the voltage V is measured differentially across the length of the conductor allowing us to drop the Δ symbol, the above vector equation reduces to the scalar equation:
the element of path along the integration of electric field vector E. If the applied E field is uniform and oriented along the length of the conductor as shown in the figure, then defining the voltage V in the usual convention of being opposite in direction to the field (see figure), and with the understanding that the voltage V is measured differentially across the length of the conductor allowing us to drop the Δ symbol, the above vector equation reduces to the scalar equation:
Since the E field is uniform in the direction of wire length, for a conductor having uniformly consistent resistivity ρ, the current density J will also be uniform in any cross-sectional area and oriented in the direction of wire length, so we may write:
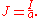
Substituting the above 2 results (for E and J respectively) into the continuum form shown at the beginning of this section:

The electrical resistance
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
of a uniform conductor is given in terms of resistivity
Resistivity
Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre...
by:
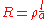
where l is the length of the conductor in SI
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
units of meters, a is the cross-sectional area (for a round wire a = πr2 if r is radius) in units of meters squared, and ρ is the resistivity in units of ohm·meters.
After substitution of R from the above equation into the equation preceding it, the continuum form of Ohm's law for a uniform field (and uniform current density) oriented along the length of the conductor reduces to the more familiar form:
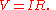
A perfect crystal lattice, with low enough thermal motion and no deviations from periodic structure, would have no resistivity
Resistivity
Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre...
, but a real metal has crystallographic defect
Crystallographic defect
Crystalline solids exhibit a periodic crystal structure. The positions of atoms or molecules occur on repeating fixed distances, determined by the unit cell parameters. However, the arrangement of atom or molecules in most crystalline materials is not perfect...
s, impurities, multiple isotope
Isotope
Isotopes are variants of atoms of a particular chemical element, which have differing numbers of neutrons. Atoms of a particular element by definition must contain the same number of protons but may have a distinct number of neutrons which differs from atom to atom, without changing the designation...
s, and thermal motion of the atoms. Electrons scatter
Scatter
In ordinary English, to scatter is to distribute randomly. Scatter also has the following meanings:*In physics, scattering is the study of collisions, especially of waves and particles...
from all of these, resulting in resistance to their flow.
The more complex generalized forms of Ohm's law are important to condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, which studies the properties of matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
and, in particular, its electronic structure. In broad terms, they fall under the topic of constitutive equations and the theory of transport coefficients.
Magnetic effects
If an external B-field is present and the conductor is not at rest but moving at velocity v, then an extra term must be added to account for the current induced by the Lorentz forceLorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
on the charge carriers.

In the rest frame
Rest frame
In special relativity the rest frame of a particle is the coordinate system in which the particle is at rest.The rest frame of compound objects is taken to be the frame of reference in which the average momentum of the particles which make up the substance is zero In special relativity the rest...
of the moving conductor this term drops out because v= 0. There is no contradiction because the electric field in the rest frame differs from the E-field in the lab frame: E ' = E + vxB.
Electric and magnetic fields are relative, see Lorentz transform.
If the current J is alternating because the applied voltage or E-field varies in time, then reactance must be added to resistance to account for self-inductance, see electrical impedance
Electrical impedance
Electrical impedance, or simply impedance, is the measure of the opposition that an electrical circuit presents to the passage of a current when a voltage is applied. In quantitative terms, it is the complex ratio of the voltage to the current in an alternating current circuit...
. The reactance may be strong if the frequency is high or the conductor is coiled.
See Hall effect
Hall effect
The Hall effect is the production of a voltage difference across an electrical conductor, transverse to an electric current in the conductor and a magnetic field perpendicular to the current...
for some other implication of a magnetic field.
History
In January 1781, before Georg OhmGeorg Ohm
Georg Simon Ohm was a German physicist. As a high school teacher, Ohm began his research with the recently-invented electrochemical cell, invented by Italian Count Alessandro Volta. Using equipment of his own creation, Ohm determined that there is a direct proportionality between the potential...
's work, Henry Cavendish
Henry Cavendish
Henry Cavendish FRS was a British scientist noted for his discovery of hydrogen or what he called "inflammable air". He described the density of inflammable air, which formed water on combustion, in a 1766 paper "On Factitious Airs". Antoine Lavoisier later reproduced Cavendish's experiment and...
experimented with Leyden jar
Leyden jar
A Leyden jar, or Leiden jar, is a device that "stores" static electricity between two electrodes on the inside and outside of a jar. It was invented independently by German cleric Ewald Georg von Kleist on 11 October 1745 and by Dutch scientist Pieter van Musschenbroek of Leiden in 1745–1746. The...
s and glass tubes of varying diameter and length filled with salt solution. He measured the current by noting how strong a shock he felt as he completed the circuit with his body. Cavendish wrote that the "velocity" (current) varied directly as the "degree of electrification" (voltage). He did not communicate his results to other scientists at the time, and his results were unknown until Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
published them in 1879.
Ohm did his work on resistance in the years 1825 and 1826, and published his results in 1827 as the book Die galvanische Kette, mathematisch bearbeitet (The galvanic Circuit investigated mathematically).
He drew considerable inspiration from Fourier
Fourier
Fourier most commonly refers to Joseph Fourier , French mathematician and physicist, or the mathematics, physics, and engineering terms named in his honor for his work on the concepts underlying them:In mathematics:...
's work on heat conduction in the theoretical explanation of his work. For experiments, he initially used voltaic pile
Voltaic pile
A voltaic pile is a set of individual Galvanic cells placed in series. The voltaic pile, invented by Alessandro Volta in 1800, was the first electric battery...
s, but later used a thermocouple
Thermocouple
A thermocouple is a device consisting of two different conductors that produce a voltage proportional to a temperature difference between either end of the pair of conductors. Thermocouples are a widely used type of temperature sensor for measurement and control and can also be used to convert a...
as this provided a more stable voltage source in terms of internal resistance and constant potential difference. He used a galvanometer to measure current, and knew that the voltage between the thermocouple terminals was proportional to the junction temperature. He then added test wires of varying length, diameter, and material to complete the circuit. He found that his data could be modeled through the equation
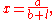
where x was the reading from the galvanometer, l was the length of the test conductor, a depended only on the thermocouple junction temperature, and b was a constant of the entire setup. From this, Ohm determined his law of proportionality and published his results.
Ohm's law was probably the most important of the early quantitative descriptions of the physics of electricity. We consider it almost obvious today. When Ohm first published his work, this was not the case; critics reacted to his treatment of the subject with hostility. They called his work a "web of naked fancies" and the German Minister of Education proclaimed that "a professor who preached such heresies was unworthy to teach science." The prevailing scientific philosophy in Germany at the time asserted that experiments need not be performed to develop an understanding of nature because nature is so well ordered, and that scientific truths may be deduced through reasoning alone. Also, Ohm's brother Martin, a mathematician, was battling the German educational system. These factors hindered the acceptance of Ohm's work, and his work did not become widely accepted until the 1840s. Fortunately, Ohm received recognition for his contributions to science well before he died.
In the 1850s, Ohm's law was known as such, and was widely considered proved, and alternatives such as "Barlow's law
Barlow's law
Barlow's law was an incorrect physical law proposed by Peter Barlow in 1824 to describe the ability of wires to conduct electricity. It said that the conductance of a wire varies inversely with the square root of its length and directly with the square root of its cross-sectional area, or:where G...
" discredited, in terms of real applications to telegraph system design, as discussed by Samuel F. B. Morse
Samuel F. B. Morse
Samuel Finley Breese Morse was an American contributor to the invention of a single-wire telegraph system based on European telegraphs, co-inventor of the Morse code, and an accomplished painter.-Birth and education:...
in 1855.
While the old term for electrical conductance, the mho
Siemens (unit)
The siemens is the SI derived unit of electric conductance and electric admittance. Conductance and admittance are the reciprocals of resistance and impedance respectively, hence one siemens is equal to the reciprocal of one ohm, and is sometimes referred to as the mho. In English, the term...
(the inverse of the resistance unit ohm), is still used, a new name, the siemens
Siemens (unit)
The siemens is the SI derived unit of electric conductance and electric admittance. Conductance and admittance are the reciprocals of resistance and impedance respectively, hence one siemens is equal to the reciprocal of one ohm, and is sometimes referred to as the mho. In English, the term...
, was adopted in 1971, honoring Ernst Werner von Siemens. The siemens is preferred in formal papers.
In the 1920s, it was discovered that the current through an ideal resistor actually has statistical fluctuations, which depend on temperature, even when voltage and resistance are exactly constant; this fluctuation, now known as Johnson–Nyquist noise
Johnson–Nyquist noise
Johnson–Nyquist noise is the electronic noise generated by the thermal agitation of the charge carriers inside an electrical conductor at equilibrium, which happens regardless of any applied voltage...
, is due to the discrete nature of charge. This thermal effect implies that measurements of current and voltage that are taken over sufficiently short periods of time will yield ratios of V/I that fluctuate from the value of R implied by the time average or ensemble average
Ensemble average
In statistical mechanics, the ensemble average is defined as the mean of a quantity that is a function of the micro-state of a system , according to the distribution of the system on its micro-states in this ensemble....
of the measured current; Ohm's law remains correct for the average current, in the case of ordinary resistive materials.
Ohm's work long preceded Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
and any understanding of frequency-dependent effects in AC circuits. Modern developments in electromagnetic theory and circuit theory do not contradict Ohm's law when they are evaluated within the appropriate limits.
See also
- Fick's law of diffusionFick's law of diffusionFick's laws of diffusion describe diffusion and can be used to solve for the diffusion coefficient, D. They were derived by Adolf Fick in the year 1855.- Fick's first law :...
- Hopkinson's law ("Ohm's Law for magnetics")
- Joule's LawJoule's lawJoule's laws are a pair of laws concerning the heat produced by a current and the energy dependence of an ideal gas to that of pressure, volume, and temperature, respectively...
P=EI - Sheet resistanceSheet resistanceSheet resistance is a measure of resistance of thin films that are namely uniform in thickness. It is commonly used to characterize materials made by semiconductor doping, metal deposition, resistive paste printing, and glass coating. Examples of these processes are: doped semiconductor regions...
- Thévenin's theoremThévenin's theoremIn circuit theory, Thévenin's theorem for linear electrical networks states that any combination of voltage sources, current sources, and resistors with two terminals is electrically equivalent to a single voltage source V and a single series resistor R. For single frequency AC systems the theorem...
- Thermal noise
External links
- John C. Shedd and Mayo D. Hershey,"The History of Ohm's Law", Popular SciencePopular SciencePopular Science is an American monthly magazine founded in 1872 carrying articles for the general reader on science and technology subjects. Popular Science has won over 58 awards, including the ASME awards for its journalistic excellence in both 2003 and 2004...
, December 1913, pages 599-614, Bonnier Corporation ISSN 0161-7370, gives the history of Ohm's investigations, prior work, Ohm's false equation in the first paper, illustration of Ohm's experimental apparatus. - Morton L. Schagrin, "Resistance to Ohm's Law", American Journal of PhysicsAmerican Journal of PhysicsThe American Journal of Physics is a monthly, peer-reviewed scientific journal published by the American Association of Physics Teachers and the American Institute of Physics. The editor is Jan Tobochnik of Kalamazoo College.-Aims and scope:...
, July 1963, Volume 31, Issue 7, pp. 536–47. Explores the conceptual change underlying Ohm's experimental work. - Kenneth L. Caneva, "Ohm, Georg Simon." Complete Dictionary of Scientific Biography. 2008

