Classical and quantum conductivity
Encyclopedia
Classical and quantum mechanical views of conductivity have both described the movements of electron
s in a metallic solid. The free electron gas that is present in metallic solids is the reason for an important property of all metals: conductivity. This article will discuss the theory of conduction, specifically the theory of classical conduction whose defects were explained by the quantum theory. The modifications that the quantum theory adds to classical conduction not only explains the flaws that arose in the classical theory, but also adds a new dimension to conduction that is currently leading to new developments in the physics world.
, a greater understanding of the physical properties of solids was achieved. Solids can be split into two groups: amorphous
and crystalline. Amorphous solid structures occur when a liquid is cooled too rapidly for the crystalline structure to form. Glass is a typical amorphous solid. When, however, ample time is allowed during the cooling of a liquid, then a crystalline structure will form. Within the category of crystalline structures, several different types of bonding are possible. These include ionic bonding, covalent bonding, and metallic bonding. The structure of a specific crystal is dependent on the bonding type, along with the sizes of the atoms involved.
Ionic crystals can form in as many as fourteen different shapes. The face-centered cubic
structure is a common shape where the crystal’s smallest unit, the unit cell, is a cube, with the smaller of the two ion
s occupying the center of each face of the cube. In the body-centered cubic structure, eight of the larger ions form a cubic shape, while one of the smaller ions occupies its center. A hexagonal
close-packed crystal structure is obtained by stacking identical spheres, and fitting these stacks into the triangular depressions of adjacent stacks.
of an ion in a crystal is dependent on the following: the square of the electric charge
of an electron
, the Boltzmann constant, the inverse of the distance between ions, as well as the Madelung constant
. The Madelung constant is the result of a mathematical sum, which is dependent on the number of ions at a certain distance from a given ion. The repelling portion of the potential energy of an ion is dependent on a constant A, and inversely, exponentially dependent on the distance between ions. By writing an equation for the total potential energy (the sum of the attractive and repulsive portions), taking its derivative with respect to the distance between ions (which is equal to the force at equilibrium separation), as well as setting that result equal to zero and using the equilibrium separation as the distance between ions, then the constant, A, can be determined. Using all of this information, a simple expression can be written for the total potential energy of the ion. Now it is dependent only on the Madelung constant, Boltzmann’s constant, the equilibrium separation, the square of the charge of an electron, and a number n (the exponential factor for the distance between ions in the repulsive portion of the potential energy). Since the equilibrium separation can be determined experimentally, and the total potential energy can be accurately estimated based on the lattice energy
of the ionic crystal, this number, n, can be determined as well.
The structure of covalently bonded crystals is determined by the directional nature of the bonds. This directional nature is a result of the specific hybridizations
that exist for different shapes.
. A Schrödinger equation
is used to display the wave function of electrons, which is dependent on the quantum numbers n and l, along with a constant, the Bohr radius
, and the distance of the electrons from an ion core. It can also be shown from the probability density
of an electron, that the electrons in a metallic solid are generally closer to the ionic cores than they were as individual atoms. This causes a decrease in the potential energy of the electrons. However, the assembly of the solid structure also confines the electrons to a smaller space than that in which they normally operate. This results in an increase in the kinetic energy
of the electrons. The stability of the structure is a result of the fact that the decrease in potential energy is much more drastic than the increase in kinetic energy. The larger the atomic radius of an atom, the greater the decrease in potential energy will be when the metal solid is formed. Also, the fewer valence electron
s an atom has, the smaller the increase in kinetic energy will be. Together these trends explain the observation that elements
to the left and lower down the periodic table
are more likely to be metals.
so well, they must contain free electrons that move through a lattice of positive ions. This motion of electrons led to the formation of Ohm's law
s, as well as related the motion in a conductor
to two types of conduction: heat and electrical. The free-moving electrons act just as a gas would; moving in every direction throughout the lattice. These electrons collide with the lattice ions as they move about, which is key in understanding thermal equilibrium
. The average velocity due to the thermal energy is zero since the electrons are going in every direction, leading to velocity vectors that are randomly oriented. What is not zero, and is in fact a high value, is the speed of these electrons, which can be calculated using the equation
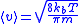
There is a way of affecting this free motion of electrons, which is by use of an electric field
. This process is known as electrical conduction. An electric field provides a potential difference along a wire of electrons, which creates a force,
, where 
is the charge of an electron and 
is the magnitude of the electric field. That force accelerates the electrons, as expected by Newton’s second law. The electrons are given a velocity away from the (negative source of the) field, which leads to these collisions with the fixed ions. The collisions rid the electrons of their kinetic energy momentarily, transferring that energy to the ion lattice in the form of heat, until the field again provides this sort of "push" to the electrons. The net result of all of this pushing and stopping (or gaining of kinetic energy and then a release of it), is a small value called drift velocity
. To better understand this concept, one could picture a busload of kids (electrons), who are energetically moving about on the bus (wire). The kids have instantaneous velocities, but after colliding with each other and bouncing back to their seats the average velocity of the kids is zero. However, as the bus moves forward, the kids have a small drift velocity in the direction of the motion of the bus. The drift that is opposite of the electric field is in fact an electric current
.
The electric current (amount of charge through a cross sectional
area per unit time) is proportional to the voltage drop
across two points, which is called Ohm’s Law and is given by
. The relationship of the current to the drift velocity as discussed above is given by 
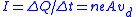, where 
is the cross sectional area,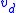 
is the drift velocity, 
is the electron charge, and 
is the number of electrons per unit volume. The reason that this equation is significant is because Ohm’s law can be written as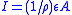 
, (or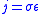 
) as well as in terms of the drift velocity 
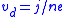. The drift velocity is much smaller than the average thermal speed of the electrons, and so the electric field has no effect on the 
of the electrons. Ohm’s law says that the resistivity
and conductivity 
must be independent of 
. This is important to the classical theory because it shows that according to Ohm’s law, since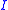 
is proportional to 
, there is a steady state situation where drift velocity is proportional to the field 
.
The entire "objective" of the classical theory is to explain resistivity in terms of the above-discussed properties of metals. By using the classical theory, one should be able to decide which metal to use for a certain purpose and be able to differentiate between different metals by use of these properties.
The journey of an electron can be expressed in another way, which is by use of the mean free path
. The mean free path λ is the average distance traveled by electrons before their collisions. An electron moves through the lattice ions of a metal, and when the electron approaches the center of an ion, there is a collision at a distance r from the center. Once it collides with an ion, the electron is now hurdled in another direction until it collides with another ion. This zigzagging formation enables the electron to have a number of collisions in time t given by naπr2vt. This distance between collisions is related to the speed and time before collisions by use of the equation λ =τ. At this point we assume the resistivity is given by ρ = (me)/(ne2λ). Notice how there is no dependence on ε, since the mean free path depends only on the size and density of the ions. The abovementioned drift velocity can be expressed in terms of the mean free path as Vd = eλε/me. One last expression, is that the mean free path is expressed by λ = (vt/naπr²vt) =1/naπr², where it is extremely important to emphasize here that the r here is the radius of those lattice ions that the electrons bounce off of.
. Furthermore, it can be shown by experiment that resistivity has a linear relationship with temperature, while the temperature in accordance to the classical theory is reliant on the value, which is related to the square root of temperature. There are some flaws from a statistical perspective as well. Applying Boltzmann statistics and the Maxwell distribution of speeds, the electrons that are viewed as particles will give an average kinetic energy of (3/2)kT. The molar heat capacity of a metal is expected to be (3/2)R greater than that of insulators, which has a heat capacity of 3R. In other words, it is expected that the molar heat capacity of metals will be (9/2)R. However, this is not observed. The experimentally determined molar heat capacity of metals is close to 3R. One last problem, (which will actually be key in the quantum solutions) is that it is known that electrons share wave-like properties as well, and the classical theory makes no mention of such properties.
, which states that since it is already known that the electrons are present in the space of the metal (i.e., something about its position is known), then there can not be zero kinetic energy (it must have some speed). This is very different from the classical viewpoint where it is assumed that at T=0 all the electrons would have a kinetic energy of zero. Also, the exclusion principle
prevents more than two electrons from being present in the lowest energy level
. This means that there are two electrons in each energy level.
In describing the quantum theory of conductivity, it is important to focus on the outermost energy level. The kinetic energy of the electrons in that last filled level is called Fermi energy
. The electrons are required to have this value of energy in order to "jump up" to the next, empty energy level. This Fermi energy is crucial in understanding the relationship between temperature and energy. When the temperature is greater than zero, some electrons will gain energy and move to higher states. Electrons gain energy from the collisions with ions, and since the kinetic energy of the lattice ions is about kT, that value is the maximum energy that an electron can gain. This means that only the electrons that are already within kT of the Fermi energy will move to the next state. Since, by the exclusion principle, there are only a few electrons in that top state that have energy close to the Fermi energy , very few electrons will gain enough energy to make that jump. That fraction of electrons excited can be given by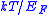
, or 
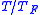where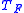 
is the Fermi temperature or temperature that provides Fermi energy. The energy contained here will increase by an order of kT. What this means is that even with an increase of T, the energy distribution is about the same as when T=0. This shows that the change in temperature is not the vital ingredient in determining energy change.
By applying these concepts and creating a new quantum understanding of conduction, the problems that existed with the classical theory now disappear. In the classical theory it was shown that the square root of was proportional to the resistivity. Now, since the net shift of velocity of all the electrons in an electric field is really the same as shifting only the Fermi electrons, in the case of thermal conductivity, the Fermi velocity can replace the in the classical equation for resistivity. Then, since there is no temperature dependency involved in the Fermi speed, there no longer exists the problem of conflicting experimental and theoretical relationships between speed and temperature.
There is one important change that must be made to ensure the validity of these equations, and that is in regard to the collisions of electrons. In the classical theory, the collision was seen as similar to that of a ball with a wall: a particle bouncing off another. In the quantum understanding, an electron is viewed as a wave traveling through a medium. When the wavelength of the electrons is larger than the crystal spacing, the electrons will propagate freely throughout the metal without collision, therefore their scattering is only the result of imperfections in the crystal lattice of the metal. These imperfections are the results of such changes as thermal vibrations. This means that the ion’s cross sectional area is no longer important, but rather the amplitude
of these vibrations and the deviations of these ions are what determines the mean free path. Fittingly, the r that was emphasized in the classical mean free path equation as being the radius of the ions, is now replaced with an r representing the amplitude of the oscillation
of those ions. The beauty of this change is that now the mean free path equation gives a linearly proportional relationship between ρ and T, and not the problematic T.05 relationship.
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s in a metallic solid. The free electron gas that is present in metallic solids is the reason for an important property of all metals: conductivity. This article will discuss the theory of conduction, specifically the theory of classical conduction whose defects were explained by the quantum theory. The modifications that the quantum theory adds to classical conduction not only explains the flaws that arose in the classical theory, but also adds a new dimension to conduction that is currently leading to new developments in the physics world.
Solid states
With the advent of quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, a greater understanding of the physical properties of solids was achieved. Solids can be split into two groups: amorphous
Amorphous solid
In condensed matter physics, an amorphous or non-crystalline solid is a solid that lacks the long-range order characteristic of a crystal....
and crystalline. Amorphous solid structures occur when a liquid is cooled too rapidly for the crystalline structure to form. Glass is a typical amorphous solid. When, however, ample time is allowed during the cooling of a liquid, then a crystalline structure will form. Within the category of crystalline structures, several different types of bonding are possible. These include ionic bonding, covalent bonding, and metallic bonding. The structure of a specific crystal is dependent on the bonding type, along with the sizes of the atoms involved.
Ionic crystals can form in as many as fourteen different shapes. The face-centered cubic
Cubic crystal system
In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals....
structure is a common shape where the crystal’s smallest unit, the unit cell, is a cube, with the smaller of the two ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s occupying the center of each face of the cube. In the body-centered cubic structure, eight of the larger ions form a cubic shape, while one of the smaller ions occupies its center. A hexagonal
Hexagonal crystal system
In crystallography, the hexagonal crystal system is one of the 7 crystal systems, the hexagonal lattice system is one of the 7 lattice systems, and the hexagonal crystal family is one of the 6 crystal families...
close-packed crystal structure is obtained by stacking identical spheres, and fitting these stacks into the triangular depressions of adjacent stacks.
Electrostatic energy
The net attractive portion of the potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
of an ion in a crystal is dependent on the following: the square of the electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
of an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, the Boltzmann constant, the inverse of the distance between ions, as well as the Madelung constant
Madelung constant
The Madelung constant is used in determining the electrostatic potential of a single ion in a crystal by approximating the ions by point charges. It is named after Erwin Madelung, a German physicist....
. The Madelung constant is the result of a mathematical sum, which is dependent on the number of ions at a certain distance from a given ion. The repelling portion of the potential energy of an ion is dependent on a constant A, and inversely, exponentially dependent on the distance between ions. By writing an equation for the total potential energy (the sum of the attractive and repulsive portions), taking its derivative with respect to the distance between ions (which is equal to the force at equilibrium separation), as well as setting that result equal to zero and using the equilibrium separation as the distance between ions, then the constant, A, can be determined. Using all of this information, a simple expression can be written for the total potential energy of the ion. Now it is dependent only on the Madelung constant, Boltzmann’s constant, the equilibrium separation, the square of the charge of an electron, and a number n (the exponential factor for the distance between ions in the repulsive portion of the potential energy). Since the equilibrium separation can be determined experimentally, and the total potential energy can be accurately estimated based on the lattice energy
Lattice energy
The lattice energy of an ionic solid is a measure of the strength of bonds in that ionic compound. It is usually defined as the enthalpy of formation of the ionic compound from gaseous ions and as such is invariably exothermic. Lattice energy may also be defined as the energy required to completely...
of the ionic crystal, this number, n, can be determined as well.
The structure of covalently bonded crystals is determined by the directional nature of the bonds. This directional nature is a result of the specific hybridizations
Orbital hybridisation
In chemistry, hybridisation is the concept of mixing atomic orbitals to form new hybrid orbitals suitable for the qualitative description of atomic bonding properties. Hybridised orbitals are very useful in the explanation of the shape of molecular orbitals for molecules. It is an integral part...
that exist for different shapes.
Quantum mechanics
Along with bonding type and atomic radii, metallic crystalline structures are also dependent on a quantum-mechanical mechanism. Unlike other crystals, in a metallically bonded solid, the electrons move freely throughout the solid, which are held in the solid by their attraction to the positively charged nucleiAtomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
. A Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
is used to display the wave function of electrons, which is dependent on the quantum numbers n and l, along with a constant, the Bohr radius
Bohr radius
The Bohr radius is a physical constant, approximately equal to the most probable distance between the proton and electron in a hydrogen atom in its ground state. It is named after Niels Bohr, due to its role in the Bohr model of an atom...
, and the distance of the electrons from an ion core. It can also be shown from the probability density
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
of an electron, that the electrons in a metallic solid are generally closer to the ionic cores than they were as individual atoms. This causes a decrease in the potential energy of the electrons. However, the assembly of the solid structure also confines the electrons to a smaller space than that in which they normally operate. This results in an increase in the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the electrons. The stability of the structure is a result of the fact that the decrease in potential energy is much more drastic than the increase in kinetic energy. The larger the atomic radius of an atom, the greater the decrease in potential energy will be when the metal solid is formed. Also, the fewer valence electron
Valence electron
In chemistry, valence electrons are the electrons of an atom that can participate in the formation of chemical bonds with other atoms. Valence electrons are the "own" electrons, present in the free neutral atom, that combine with valence electrons of other atoms to form chemical bonds. In a single...
s an atom has, the smaller the increase in kinetic energy will be. Together these trends explain the observation that elements
Chemical element
A chemical element is a pure chemical substance consisting of one type of atom distinguished by its atomic number, which is the number of protons in its nucleus. Familiar examples of elements include carbon, oxygen, aluminum, iron, copper, gold, mercury, and lead.As of November 2011, 118 elements...
to the left and lower down the periodic table
Periodic table
The periodic table of the chemical elements is a tabular display of the 118 known chemical elements organized by selected properties of their atomic structures. Elements are presented by increasing atomic number, the number of protons in an atom's atomic nucleus...
are more likely to be metals.
Classical conductivity
Around 1900, Paul Drude developed the foundation for classical conduction. He reasoned that since metals conduct electricityElectricity
Electricity is a general term encompassing a variety of phenomena resulting from the presence and flow of electric charge. These include many easily recognizable phenomena, such as lightning, static electricity, and the flow of electrical current in an electrical wire...
so well, they must contain free electrons that move through a lattice of positive ions. This motion of electrons led to the formation of Ohm's law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
s, as well as related the motion in a conductor
Electrical conductor
In physics and electrical engineering, a conductor is a material which contains movable electric charges. In metallic conductors such as copper or aluminum, the movable charged particles are electrons...
to two types of conduction: heat and electrical. The free-moving electrons act just as a gas would; moving in every direction throughout the lattice. These electrons collide with the lattice ions as they move about, which is key in understanding thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
. The average velocity due to the thermal energy is zero since the electrons are going in every direction, leading to velocity vectors that are randomly oriented. What is not zero, and is in fact a high value, is the speed of these electrons, which can be calculated using the equation
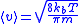
There is a way of affecting this free motion of electrons, which is by use of an electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
. This process is known as electrical conduction. An electric field provides a potential difference along a wire of electrons, which creates a force,
, where is the charge of an electron and is the magnitude of the electric field. That force accelerates the electrons, as expected by Newton’s second law. The electrons are given a velocity away from the (negative source of the) field, which leads to these collisions with the fixed ions. The collisions rid the electrons of their kinetic energy momentarily, transferring that energy to the ion lattice in the form of heat, until the field again provides this sort of "push" to the electrons. The net result of all of this pushing and stopping (or gaining of kinetic energy and then a release of it), is a small value called drift velocityDrift velocity
The drift velocity is the average velocity that a particle, such as an electron, attains due to an electric field. It can also be referred to as Axial Drift Velocity since particles defined are assumed to be moving along a plane. In general, an electron will 'rattle around' in a conductor at the...
. To better understand this concept, one could picture a busload of kids (electrons), who are energetically moving about on the bus (wire). The kids have instantaneous velocities, but after colliding with each other and bouncing back to their seats the average velocity of the kids is zero. However, as the bus moves forward, the kids have a small drift velocity in the direction of the motion of the bus. The drift that is opposite of the electric field is in fact an electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
.
The electric current (amount of charge through a cross sectional
Cross section (physics)
A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
area per unit time) is proportional to the voltage drop
Voltage drop
Voltage drop is the reduction in voltage in the passive elements of an electrical circuit. Voltage drops across conductors, contacts, connectors and source internal resistances are undesired as they reduce the supplied voltage while voltage drops across loads and other electrical and electronic...
across two points, which is called Ohm’s Law and is given by
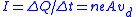. The relationship of the current to the drift velocity as discussed above is given by , where is the cross sectional area, 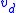is the drift velocity, is the electron charge, and is the number of electrons per unit volume. The reason that this equation is significant is because Ohm’s law can be written as 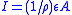, (or 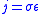) as well as in terms of the drift velocity 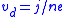. The drift velocity is much smaller than the average thermal speed of the electrons, and so the electric field has no effect on the of the electrons. Ohm’s law says that the resistivityResistivity
Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre...
and conductivity must be independent of . This is important to the classical theory because it shows that according to Ohm’s law, since 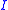is proportional to , there is a steady state situation where drift velocity is proportional to the field .The entire "objective" of the classical theory is to explain resistivity in terms of the above-discussed properties of metals. By using the classical theory, one should be able to decide which metal to use for a certain purpose and be able to differentiate between different metals by use of these properties.
The journey of an electron can be expressed in another way, which is by use of the mean free path
Mean free path
In physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:...
. The mean free path λ is the average distance traveled by electrons before their collisions. An electron moves through the lattice ions of a metal, and when the electron approaches the center of an ion, there is a collision at a distance r from the center. Once it collides with an ion, the electron is now hurdled in another direction until it collides with another ion. This zigzagging formation enables the electron to have a number of collisions in time t given by naπr2vt. This distance between collisions is related to the speed and time before collisions by use of the equation λ =
Flaws in classical conductivity
While the classical understanding of conduction is useful in constructing Ohm’s law and providing an understanding of the motion of electrons, there are a number of inherent flaws in this theory. Firstly, the above stated equation for resistivity will give a value that is about seven times the measured value of resistivity at a temperature of 300 KKelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
. Furthermore, it can be shown by experiment that resistivity has a linear relationship with temperature, while the temperature in accordance to the classical theory is reliant on the value
Quantum conductivity
Before explaining how the quantum theory solves these flaws, there are a number of concepts that need to be understood. The first concept is that of the uncertainty principleUncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
, which states that since it is already known that the electrons are present in the space of the metal (i.e., something about its position is known), then there can not be zero kinetic energy (it must have some speed). This is very different from the classical viewpoint where it is assumed that at T=0 all the electrons would have a kinetic energy of zero. Also, the exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
prevents more than two electrons from being present in the lowest energy level
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
. This means that there are two electrons in each energy level.
In describing the quantum theory of conductivity, it is important to focus on the outermost energy level. The kinetic energy of the electrons in that last filled level is called Fermi energy
Fermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
. The electrons are required to have this value of energy in order to "jump up" to the next, empty energy level. This Fermi energy is crucial in understanding the relationship between temperature and energy. When the temperature is greater than zero, some electrons will gain energy and move to higher states. Electrons gain energy from the collisions with ions, and since the kinetic energy of the lattice ions is about kT, that value is the maximum energy that an electron can gain. This means that only the electrons that are already within kT of the Fermi energy will move to the next state. Since, by the exclusion principle, there are only a few electrons in that top state that have energy close to the Fermi energy , very few electrons will gain enough energy to make that jump. That fraction of electrons excited can be given by
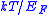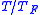, or where 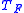is the Fermi temperature or temperature that provides Fermi energy. The energy contained here will increase by an order of kT. What this means is that even with an increase of T, the energy distribution is about the same as when T=0. This shows that the change in temperature is not the vital ingredient in determining energy change.By applying these concepts and creating a new quantum understanding of conduction, the problems that existed with the classical theory now disappear. In the classical theory it was shown that the square root of
There is one important change that must be made to ensure the validity of these equations, and that is in regard to the collisions of electrons. In the classical theory, the collision was seen as similar to that of a ball with a wall: a particle bouncing off another. In the quantum understanding, an electron is viewed as a wave traveling through a medium. When the wavelength of the electrons is larger than the crystal spacing, the electrons will propagate freely throughout the metal without collision, therefore their scattering is only the result of imperfections in the crystal lattice of the metal. These imperfections are the results of such changes as thermal vibrations. This means that the ion’s cross sectional area is no longer important, but rather the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of these vibrations and the deviations of these ions are what determines the mean free path. Fittingly, the r that was emphasized in the classical mean free path equation as being the radius of the ions, is now replaced with an r representing the amplitude of the oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
of those ions. The beauty of this change is that now the mean free path equation gives a linearly proportional relationship between ρ and T, and not the problematic T.05 relationship.