
Dyadic rational
Encyclopedia
In mathematics
, a dyadic fraction or dyadic rational is a rational number
whose denominator is a power of two
, i.e., a number of the form a/2b where a is an integer
and b is a natural number
; for example, 1/2 or 3/8, but not 1/3. These are precisely the numbers whose binary
expansion is finite.
The inch is customarily subdivided in dyadic rather than decimal fractions; similarly, the customary divisions of the gallon
into half-gallons, quart
s, and pint
s are dyadic. The ancient Egyptians also used dyadic fractions in measurement, with denominators up to 1/64, using a notation based on the Eye of Horus
(see, e.g., Curtis).
The set of all dyadic fractions is dense
in the real line
: any real number x can be arbitrarily closely approximated by dyadic rationals of the form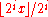 .
.
Compared to other dense subsets of the real line, such as the rational numbers, the dyadic rationals are in some sense a relatively "small" dense set, which is why they sometimes occur in proofs. (See for instance Urysohn's lemma
.)
The sum
, product
, or difference
of any two dyadic fractions is itself another dyadic fraction:
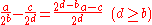


However, the result of dividing
one dyadic fraction by another is, in general, not a dyadic fraction. Thus, the dyadic fractions form a subring
of the rational numbers Q
. Algebraically, this subring is the localization
of the integers Z with respect to the set of powers of two.
The surreal number
s are generated by an iterated construction principle which starts by generating all finite dyadic fractions, and then goes on to create new and strange kinds of infinite, infinitesimal and other numbers.
the dyadic rationals are the direct limit
of infinite cyclic subgroups of the rational numbers,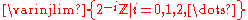
In the spirit of Pontryagin duality
, there is a dual object, namely the inverse limit
of the unit circle
group under the repeated squaring map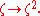
The resulting dual is a topological group
D called the dyadic solenoid, an example of a solenoid group.
An element of the dyadic solenoid can be represented as an infinite sequence of complex numbers q0, q1, q2, ..., with the properties that each qi lies on the unit circle and that, for all i > 0, qi2 = qi-1. The group operation on these elements multiplies any two sequences componentwise.
As a topological space the dyadic solenoid is an indecomposable continuum
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a dyadic fraction or dyadic rational is a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
whose denominator is a power of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
, i.e., a number of the form a/2b where a is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
and b is a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
; for example, 1/2 or 3/8, but not 1/3. These are precisely the numbers whose binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
expansion is finite.
The inch is customarily subdivided in dyadic rather than decimal fractions; similarly, the customary divisions of the gallon
Gallon
The gallon is a measure of volume. Historically it has had many different definitions, but there are three definitions in current use: the imperial gallon which is used in the United Kingdom and semi-officially within Canada, the United States liquid gallon and the lesser used United States dry...
into half-gallons, quart
Quart
The quart is a unit of volume equal to a quarter of a gallon, two pints, or four cups. Since gallons of various sizes have historically been in use, quarts of various sizes have also existed; see gallon for further discussion. Three of these kinds of quarts remain in current use, all approximately...
s, and pint
Pint
The pint is a unit of volume or capacity that was once used across much of Europe with values varying from state to state from less than half a litre to over one litre. Within continental Europe, the pint was replaced with the metric system during the nineteenth century...
s are dyadic. The ancient Egyptians also used dyadic fractions in measurement, with denominators up to 1/64, using a notation based on the Eye of Horus
Eye of Horus
The Eye of Horus is an ancient Egyptian symbol of protection, royal power and good health. The eye is personified in the goddess Wadjet...
(see, e.g., Curtis).
The set of all dyadic fractions is dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
: any real number x can be arbitrarily closely approximated by dyadic rationals of the form
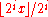 .
.Compared to other dense subsets of the real line, such as the rational numbers, the dyadic rationals are in some sense a relatively "small" dense set, which is why they sometimes occur in proofs. (See for instance Urysohn's lemma
Urysohn's lemma
In topology, Urysohn's lemma is a lemma that states that a topological space is normal if and only if any two disjoint closed subsets can be separated by a function....
.)
The sum
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, product
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, or difference
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
of any two dyadic fractions is itself another dyadic fraction:

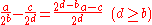


However, the result of dividing
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
one dyadic fraction by another is, in general, not a dyadic fraction. Thus, the dyadic fractions form a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of the rational numbers Q
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
. Algebraically, this subring is the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of the integers Z with respect to the set of powers of two.
The surreal number
Surreal number
In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number...
s are generated by an iterated construction principle which starts by generating all finite dyadic fractions, and then goes on to create new and strange kinds of infinite, infinitesimal and other numbers.
Dyadic solenoid
As an additive abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
the dyadic rationals are the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of infinite cyclic subgroups of the rational numbers,
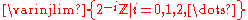
In the spirit of Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
, there is a dual object, namely the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
group under the repeated squaring map
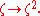
The resulting dual is a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
D called the dyadic solenoid, an example of a solenoid group.
An element of the dyadic solenoid can be represented as an infinite sequence of complex numbers q0, q1, q2, ..., with the properties that each qi lies on the unit circle and that, for all i > 0, qi2 = qi-1. The group operation on these elements multiplies any two sequences componentwise.
As a topological space the dyadic solenoid is an indecomposable continuum
Indecomposable continuum
In point-set topology, an indecomposable continuum is a continuum that is not the union of any two of its proper subcontinua. The pseudo-arc is an example of a hereditarily indecomposable continuum. L. E. J...
.
See also
- p-adic numberP-adic numberIn mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
- local ringLocal ringIn abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
- Bernoulli processBernoulli processIn probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables Xi are identical and independent...
- equidistribution theoremEquidistribution theoremIn mathematics, the equidistribution theorem is the statement that the sequenceis uniformly distributed on the unit interval, when a is an irrational number...

